计算物理期末论文

计算物理

---

摘要

　　之前的各项工作中，我们所研究的重点都是有确定性的系统（deterministic），而在第七章中，我们将考虑一种随机性占据主导的系统，我们称之为随机系统。
　　本次期末论文将进一步探究随机系统的种种特性。

背景

　　我们研究具有确定性的系统时，常通过数学工具，结合物理公式，来进行研究，例如牛顿运动定律及有边界条件的微分方程，而此类方程解是确定的。在此类系统中，我们给定初始值，则该系统之后的运动情况都将确定。
　　但实际情况中，我们还常常接触到另一种运动形式，即随机运动
　　例如我们常见的骰子，
　　
　　理论上而言，每面朝上的概率都是相等的，即$1/6$，因此我们每次掷骰子时，都无法预测哪一面朝上。
　　另一个典型的例子就是布朗运动。布朗运动在物理学史上的重要意义不必赘述，它充分展示了水分子的运动是无序的，从而对统计物理尤其是涨落理论的发展起到推动作用
　　
　　对于此类系统，尽管他们仍然遵循各种力学规律，如布朗运动中分子间的碰撞，但是想要和之前的系统一样精确计算已经不太可能，因为会带来庞大的计算量。为此我们将尝试用概率论来描述该系统，我们将采用较大的样本数量，和较长的运行时间，从而使结果更加趋于真实

正文

1. 随机行走

1.1 一维状态
　　 这里我们假设一个微观粒子，它在下一时刻向左或向右运动的概率相等，若我们统计他走过的位移，得到的便是以为随机行走的模型
　　 我们的程序将产生一个0到1之间的随机数组，如过大于0.5则向左走，反之向右
　　 程序代码如下随机行走-1D
　　
　　
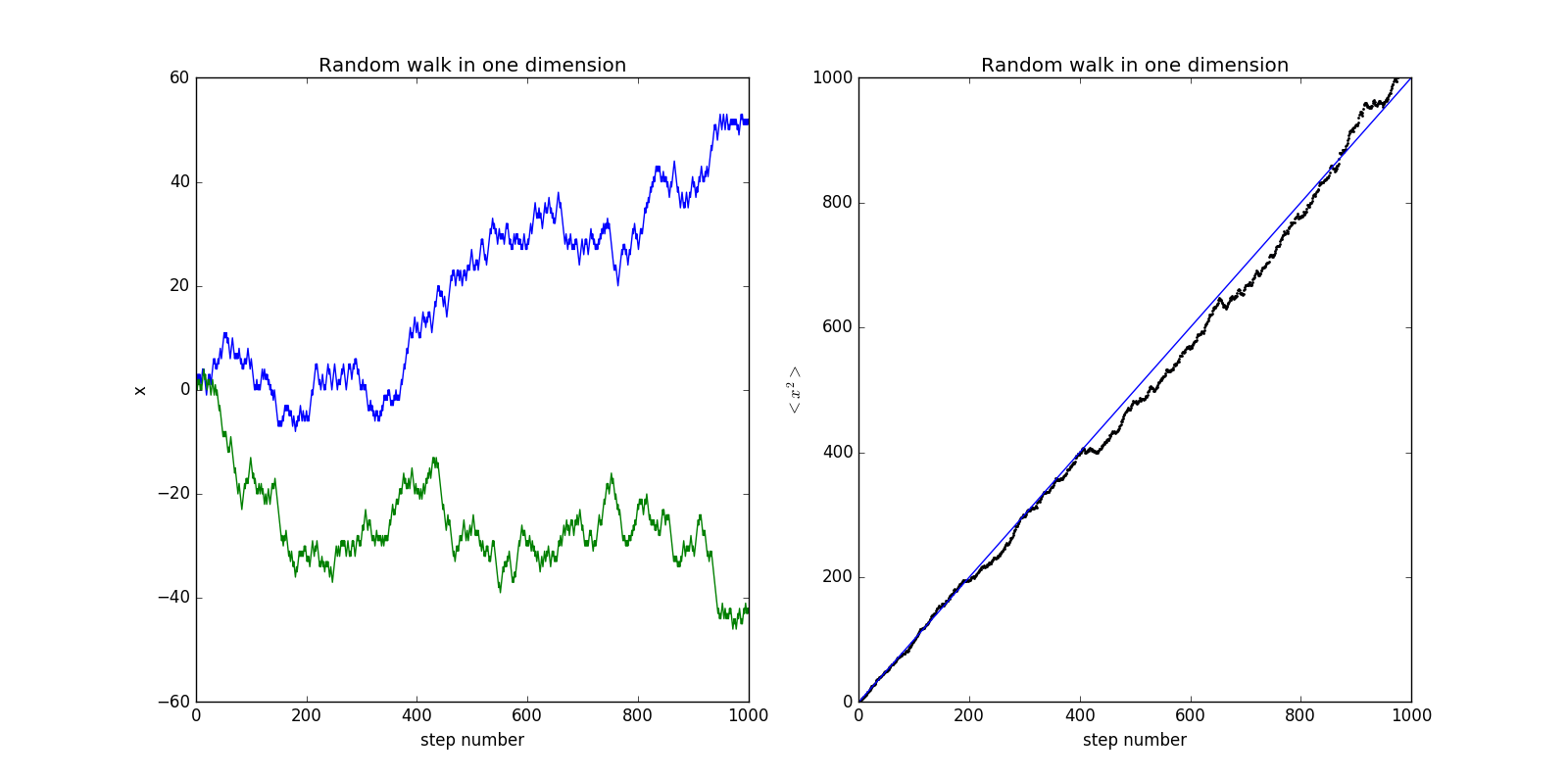
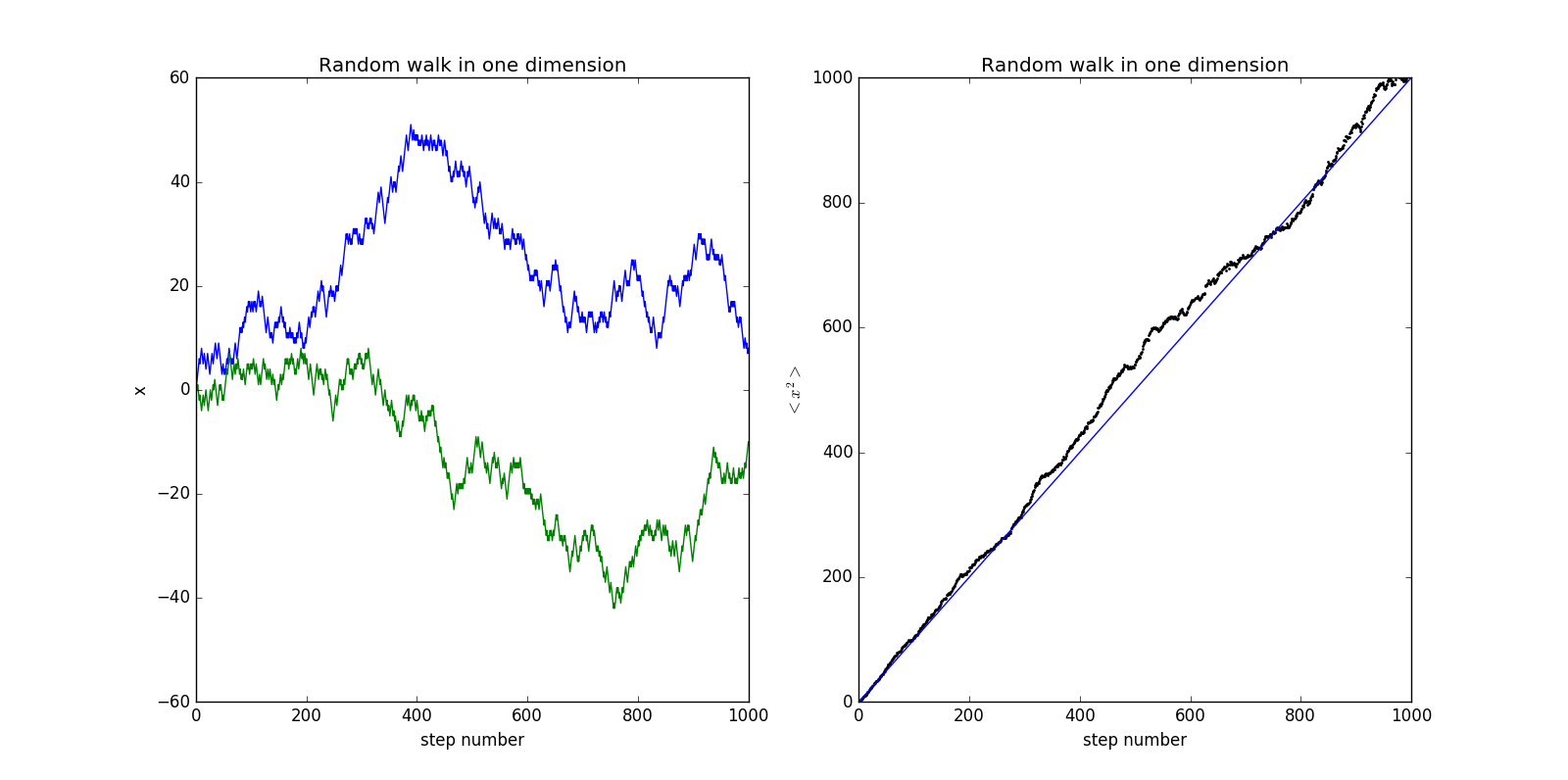
这里我们可以尝试改变两个方向的概率，如向左走的概率为0.25，向右走的概率为0.75，情况会大不相同，结果如下

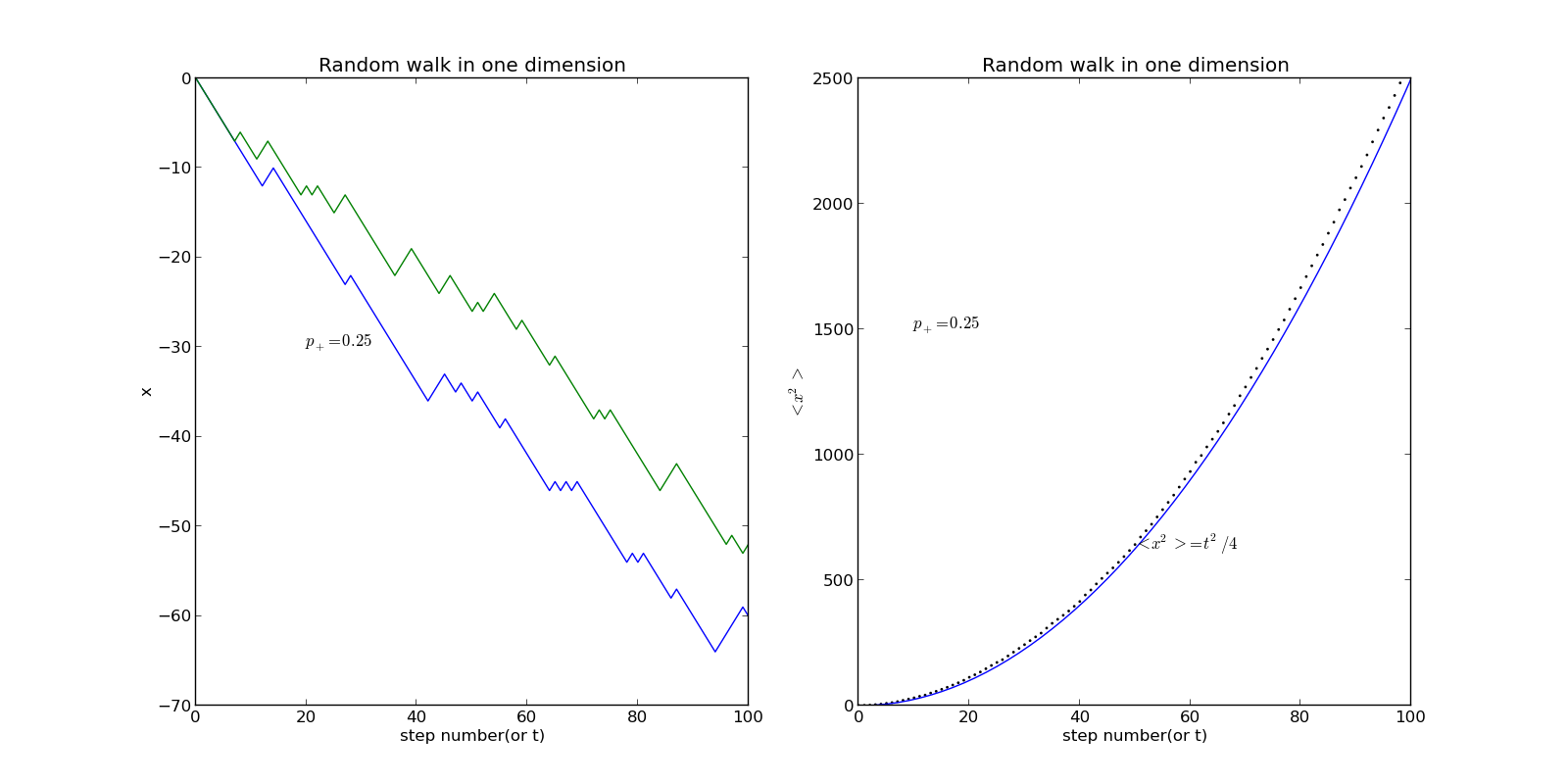
　　 这时我们考虑另一种随机行走模式，及每两步之间的差值在-1到1之间，我们称此模型为随机步长
　　 程序代码如下随机步长


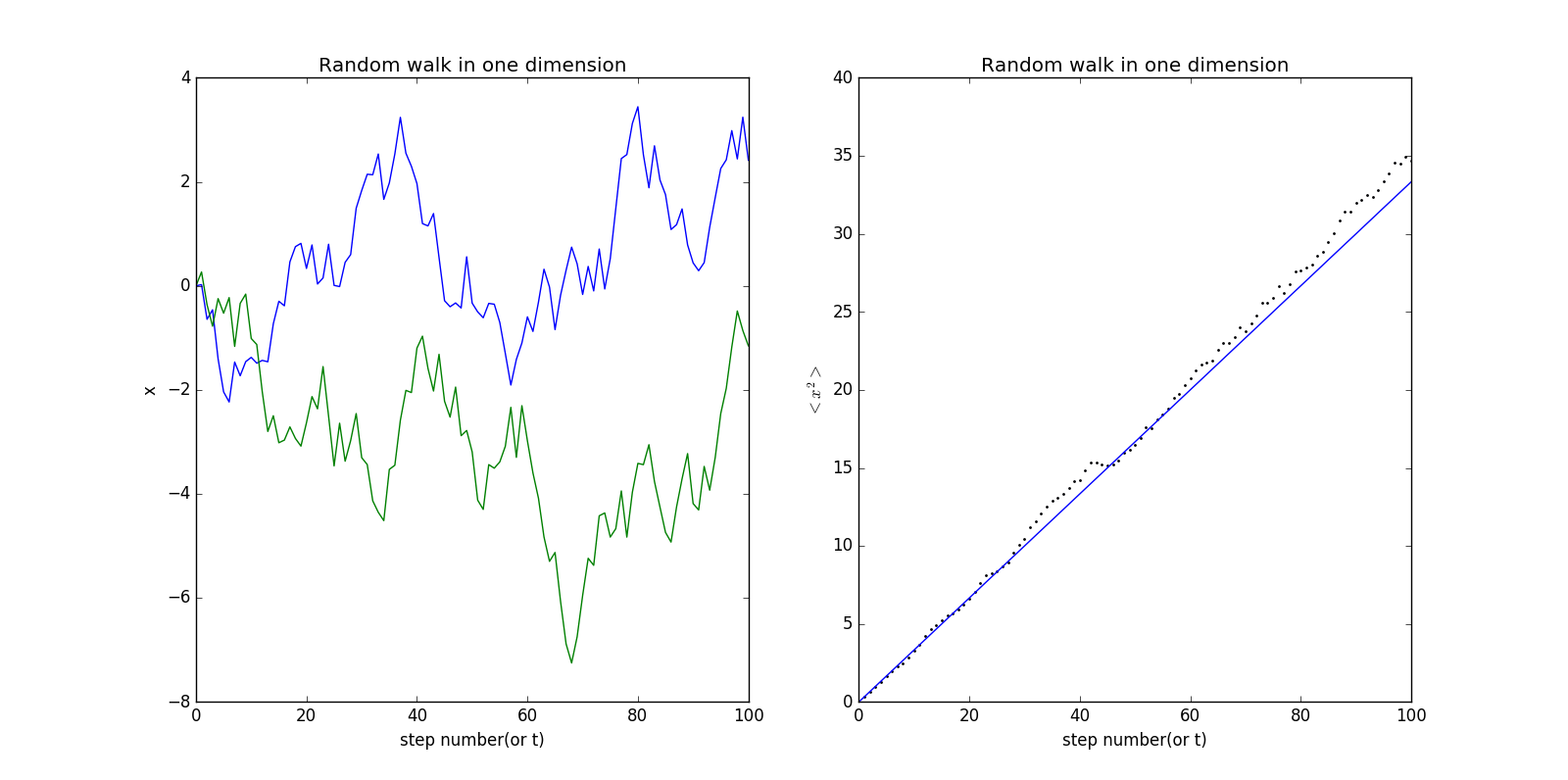
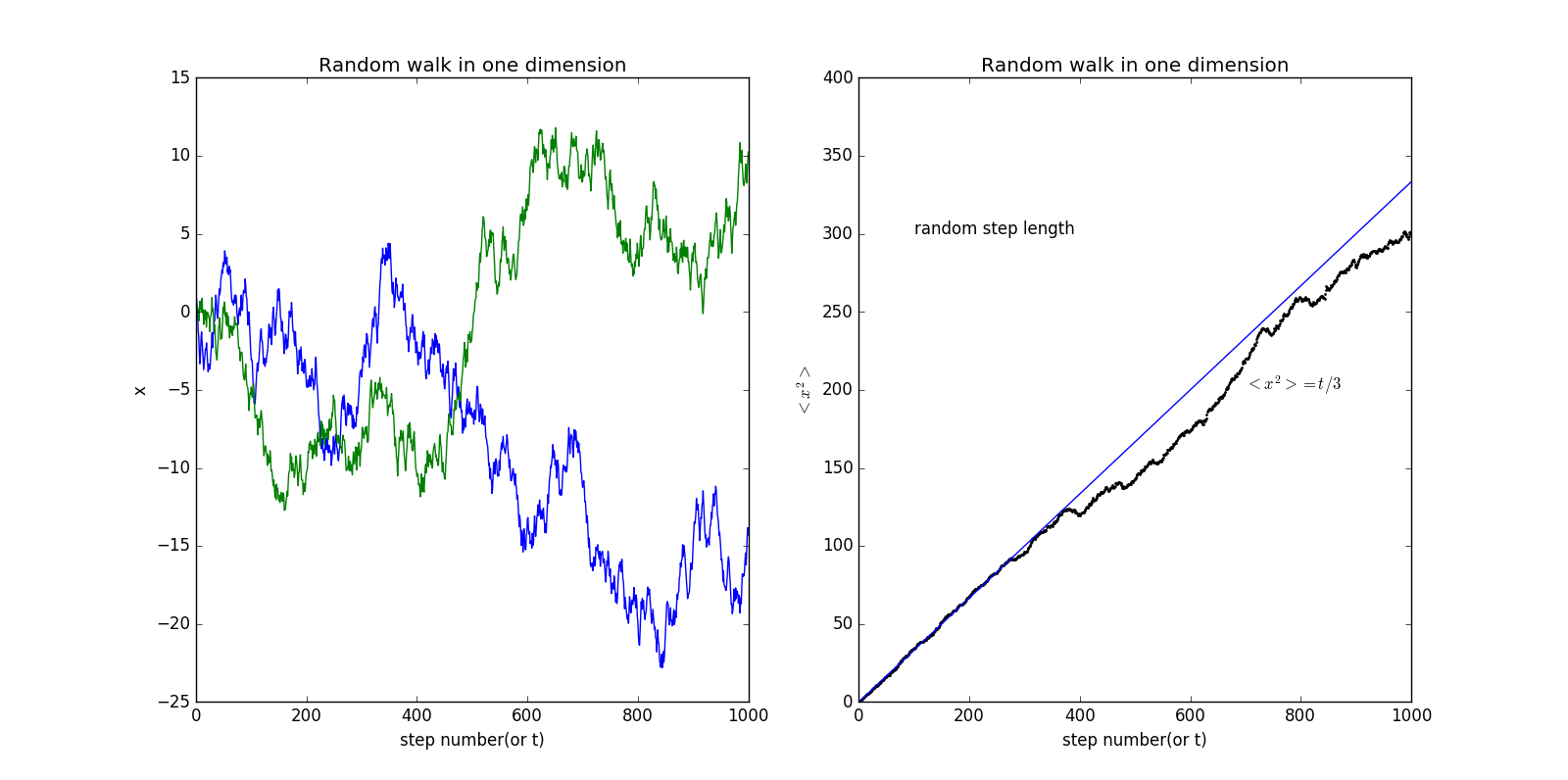
1.2 二维状态　　
　　对于二维的随机行走，我们可以采用创建两个数组构成二维数组来表示，代码如下：二维
　　1000步
　　
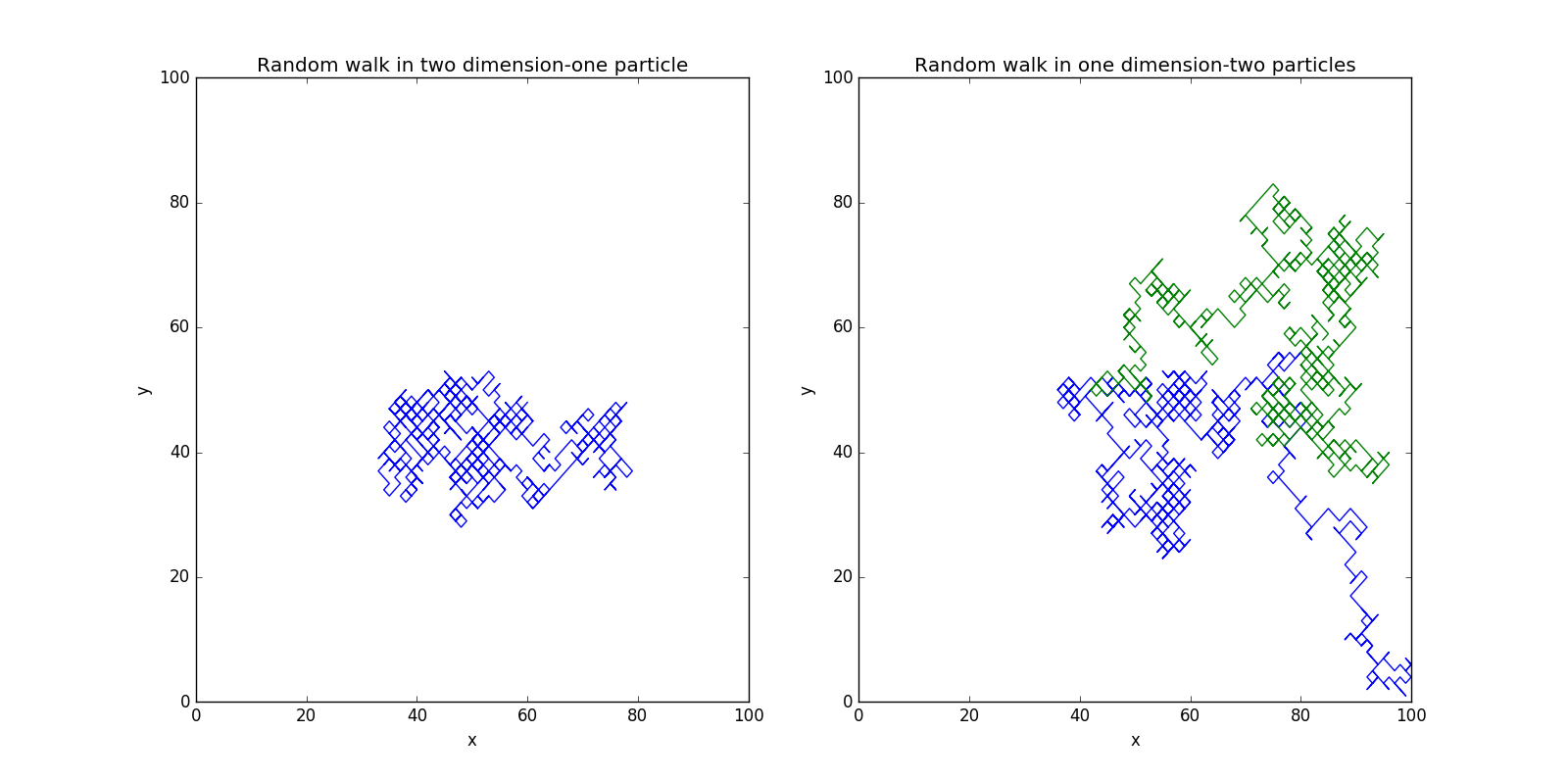
　　100000步
　　
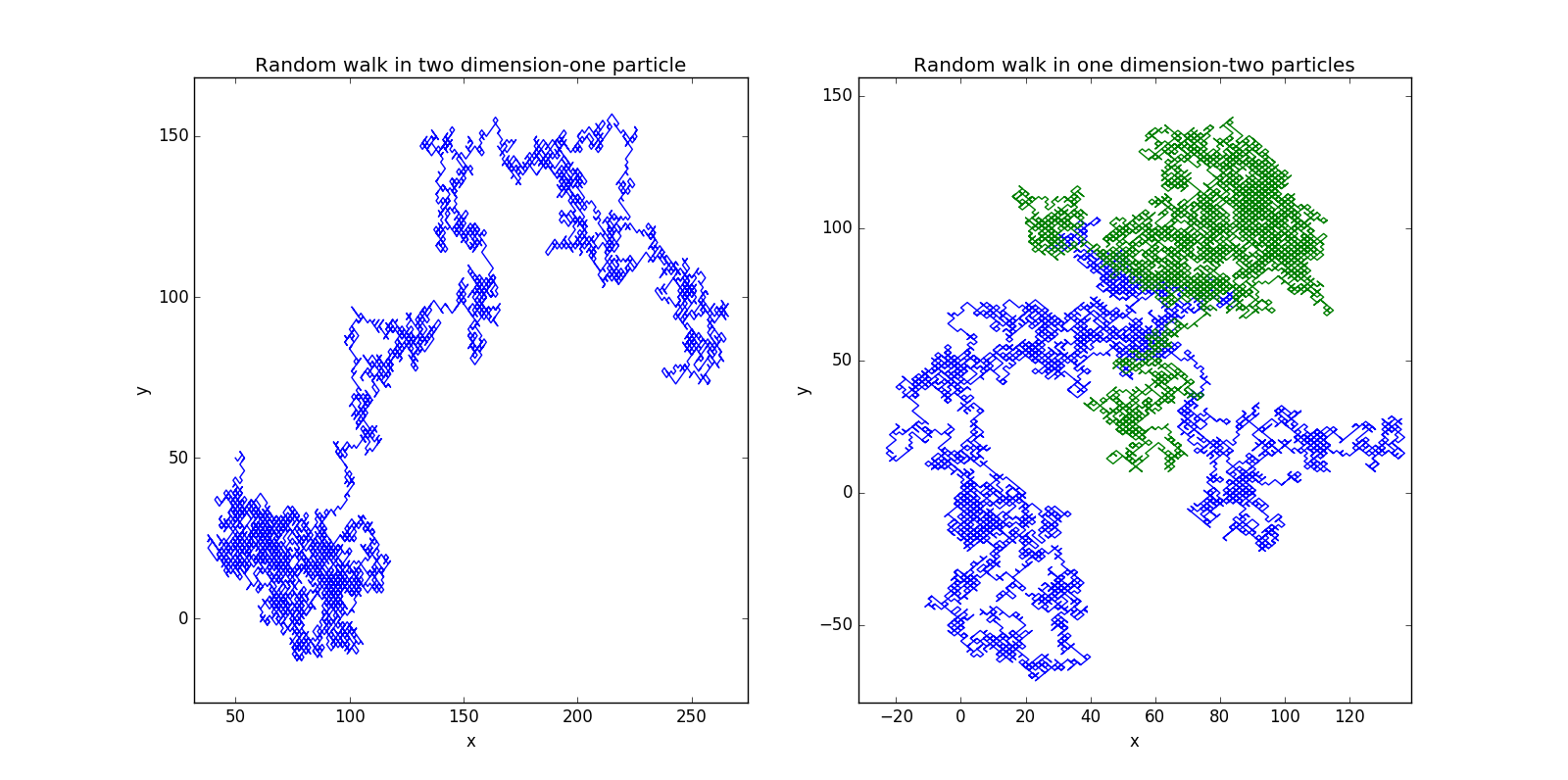
可见二维的情况有点类似布朗运动的程序模拟
1.3 三维状态
　　更进一步的，我们可以研究三维情况下的随机行走模型，代码如下：三维
　　100步
　　
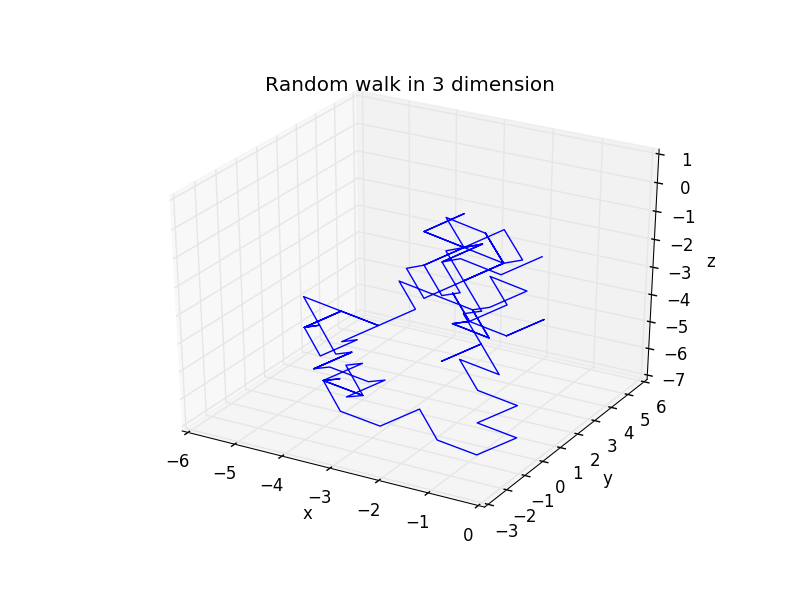
　　1000步
　　
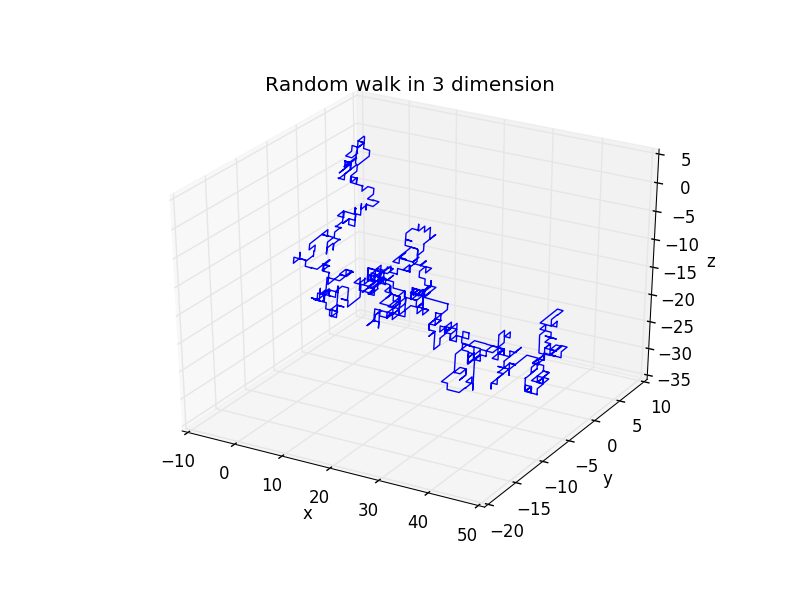
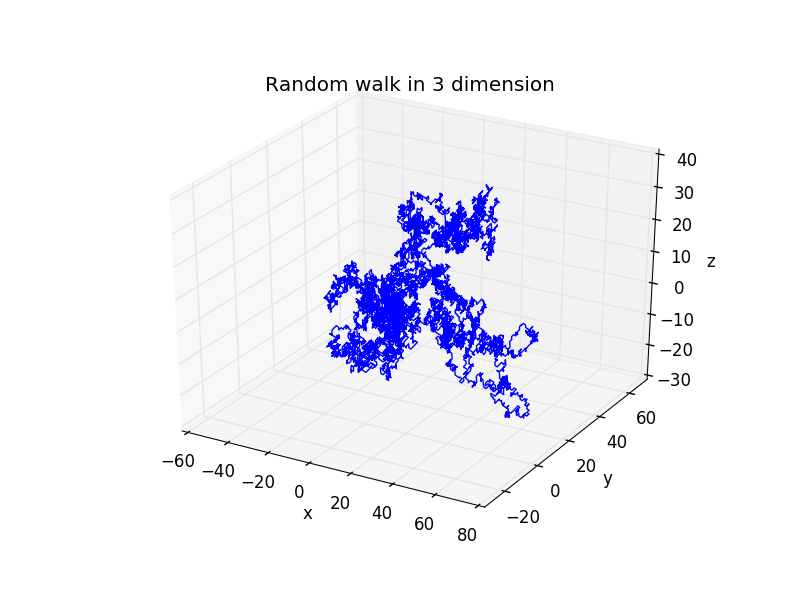
　　10000步
　　
我们也可以观察此时的 $r^2$ 与 $t$ 的关系

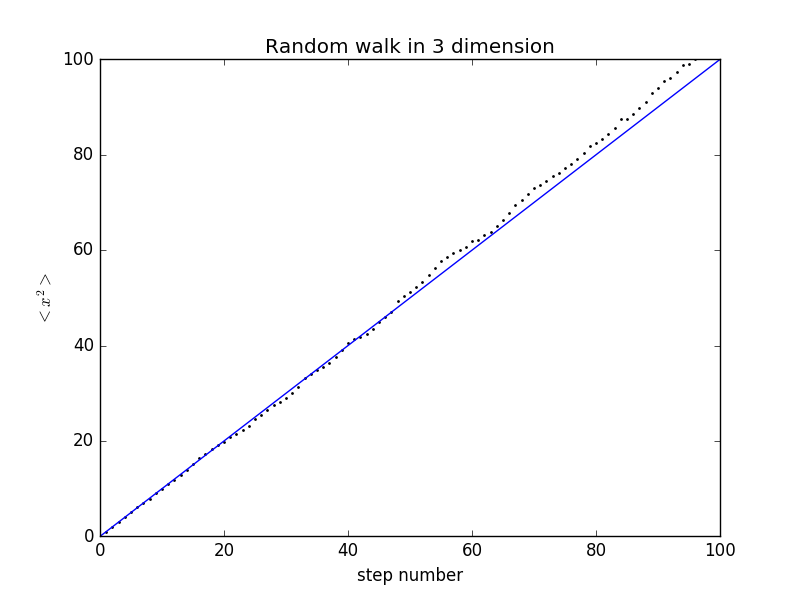
不难看出，在各个方向行走概率相同的时候，两者是呈线性相关的

1.4 延伸
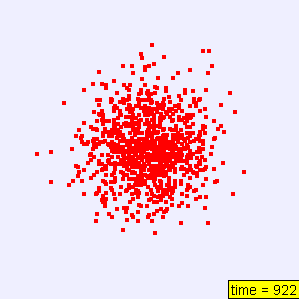
　　在一维状态下，若我们同时释放多个粒子，并且记录各个粒子和中心点的位移，我们又会有新的发现。这一过程我们借助热力学与统计力学中的Java程序进行描绘。结果如下：
　　
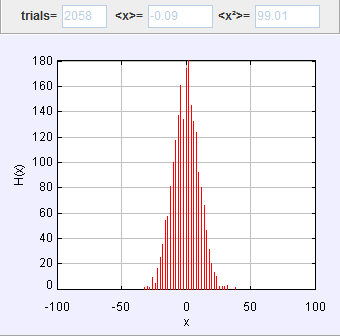
　　我们发现，从某种意义上讲，这个结果更近似与高斯分布，这或许暗示我们其中有某些更深层次的数学关系，我们将在下一部分做进一步探讨

2. 随机行走与扩散

对于一个三维模型而言，下一秒移动的方向有六种可能性，则在第n秒时，到达固定点（i,j,k）的概率为

$$\begin{eqnarray*} P(i,j,k)&=&\frac{1}{6}[P(i+1,j,k,n-1)+P(i-1,j,k,n-1)+P(i,j+1,k,n-1)+P(i,j-1,k,n-1)+P(i,j,k+1,n-1)+[P(i,j,k-1,n-1)]\\ \end{eqnarray*}$$
因此
$$\begin{eqnarray*} P(i,j,k,n)&-&P(i,j,k,n-1)=\\ &\frac16&{[P(i+1,j,k,n-1)-2P(i,j,k,n-1)+P(i-1,j,k,n-1)]\\ +[P(i,j+1,k,n-1)-2P(i,j,k,n-1)+P(i,j-1,k,n-1)]\\ +[P(i,j,k+1,n-1)-2P(i,j,k,n-1)+P(i,j,k-1,n-1)]} \end{eqnarray*}$$
由此，我们得到：
$$\begin{eqnarray*} \frac{\partial P(x,y,z,t)}{\partial t}=D\nabla ^2P(x,y,z,t)\\ \end{eqnarray*}$$
进一步的：
$$\begin{eqnarray*} \frac{\partial \rho}{\partial t}=F\frac{\partial^2\rho}{\partial x^2} \end{eqnarray*}$$
$$\begin{eqnarray*} \frac{\rho(i,n+1)-\rho(i,n)}{\Delta t}=\frac{\rho(i+1,n)-2\rho(i,n)+\rho(i-1,n)}{(\Delta x)^2} \end{eqnarray*}$$
$$\begin{eqnarray*} \rho(i,n+1)=\rho(i,n)+\frac{D\Delta t}{(\Delta x)^2}[\rho(i+1,n)+\rho(i-1,n)-2\rho(i,n)] \end{eqnarray*}$$

2.1 一般情况
　　在某种意义上，随机行走可以等同于扩散，其实在热力学与统计力学课上，我们便通过一Java程序，了解了此过程。
　　
　　在这里，我们将试图用Python，来重现这一过程
　　我们的代码如下：扩散
　　程序运行结果如下：
　　
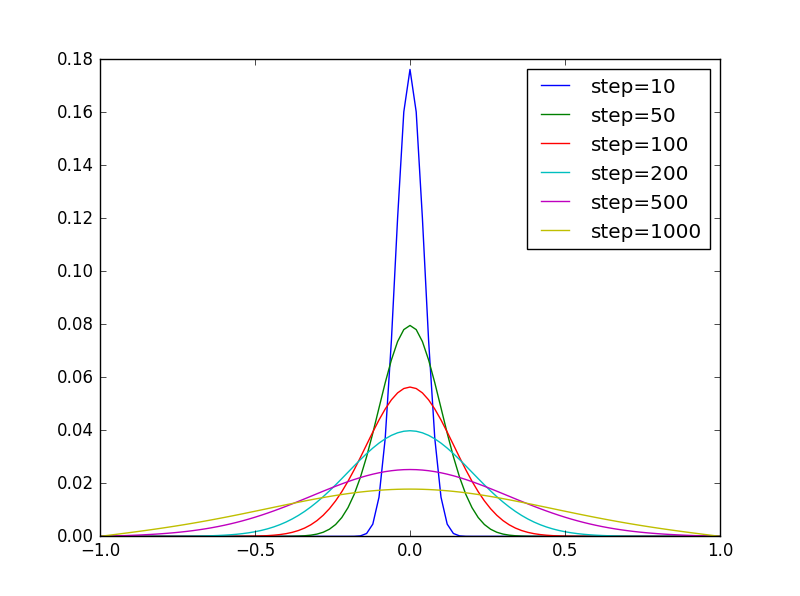
　　我们发现，其分布近似可写作一高斯分布函数：
　　

$$\begin{eqnarray*} 　　\rho(x,t)=\frac{1}{\sigma}esp[-\frac{x^2}{2\sigma^2} ] 　　\end{eqnarray*}$$
　　这一结果不禁令我们联想到之前的猜测，即多粒子体系的随机运动，其结果最终光辉满足高斯分布。
　　
2.2 3D模拟图像
　　为了更直观的看到整个变化过程，我们可以将程序修改成3D图像，最终结果如下：
　　t=0
　　
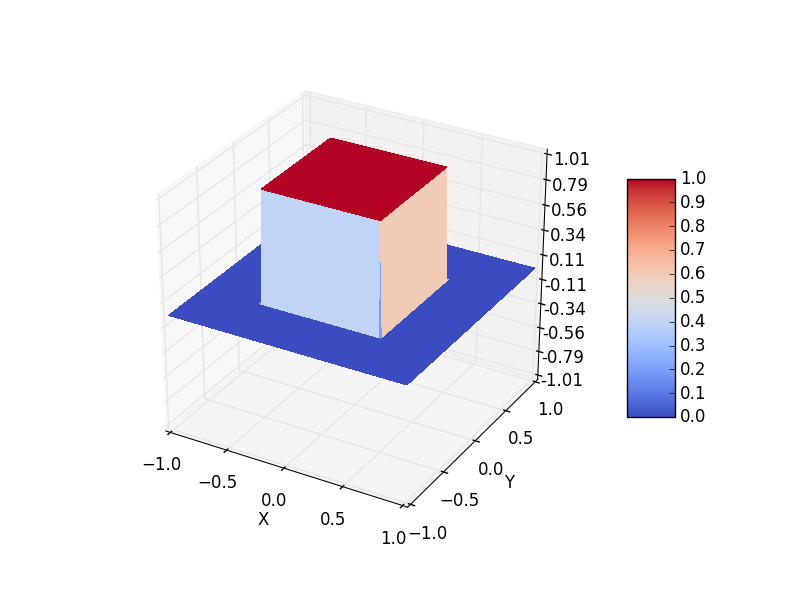
　　t=10
　　
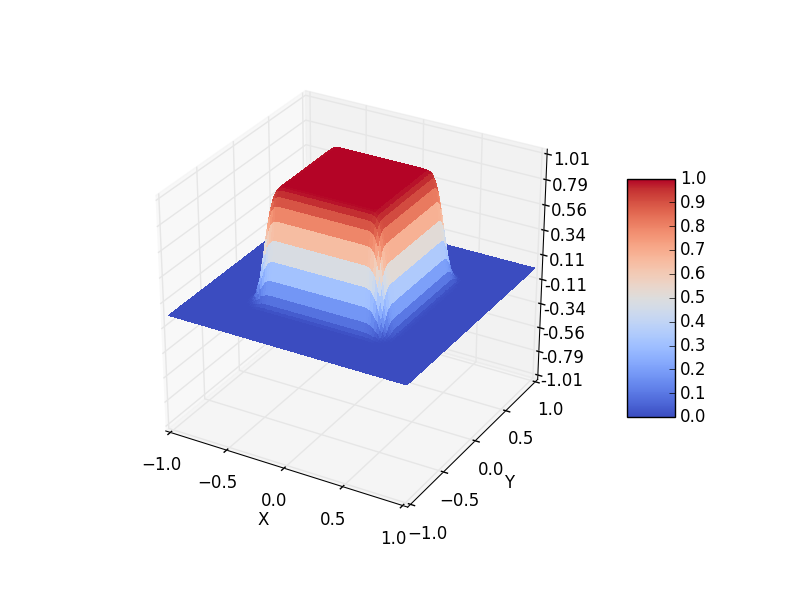
　　t=100
　　
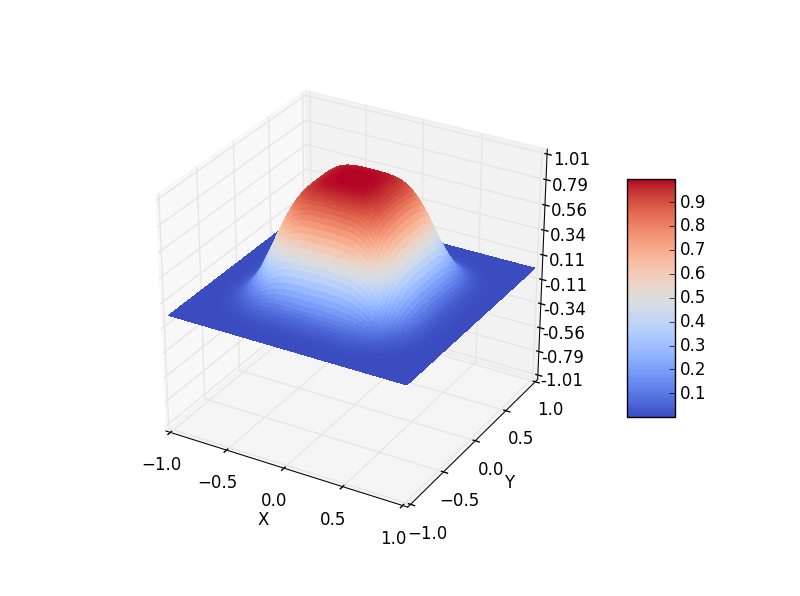
　　t=500
　　
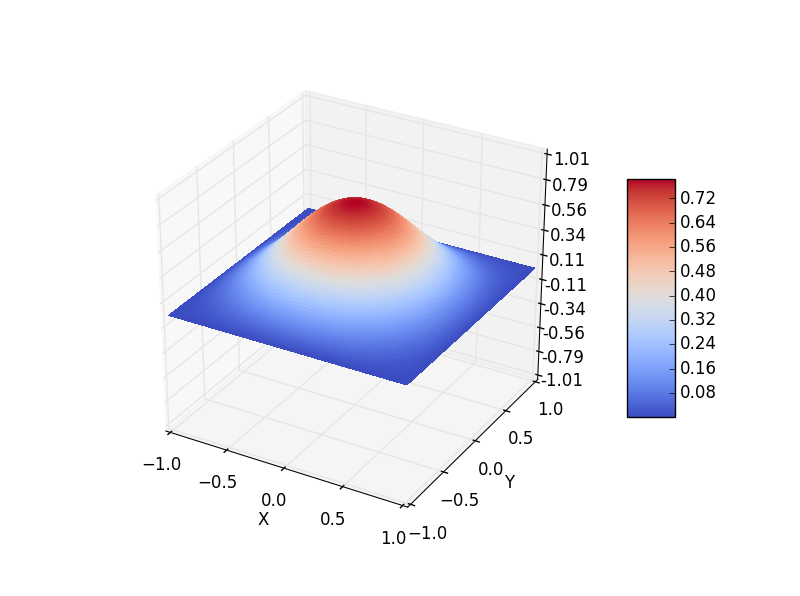
　　t=1000
　　
　　

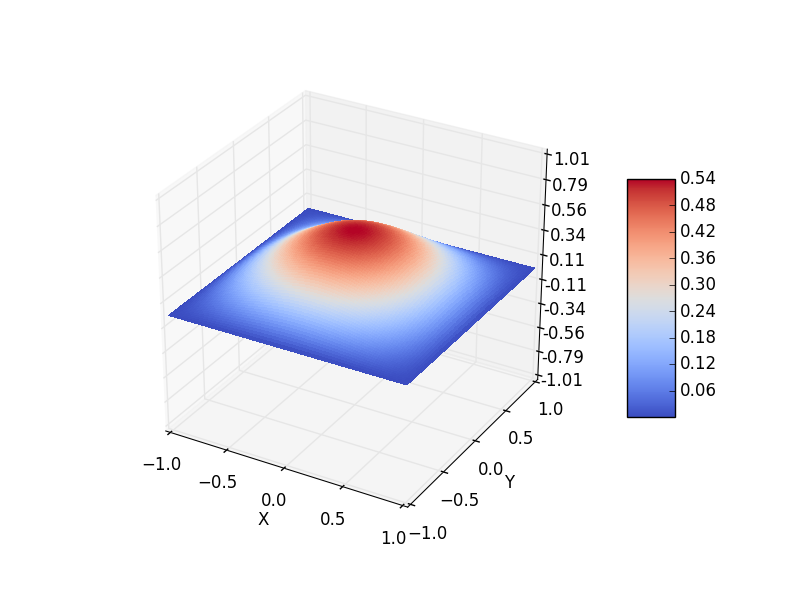
3. 扩散、熵和时间的方向

由热统的知识可知，熵的定义为

$$S=-\sum_i^nP_ilnP_i$$

　　正如我们上一部分开头利用Java所展示的扩散过程，我们接下来将对这一类型的扩散进行讨论。这里我们取咖啡中奶油的扩散为研究模型，研究系统熵的变化情况
　　Java程序模拟：
　　
　　
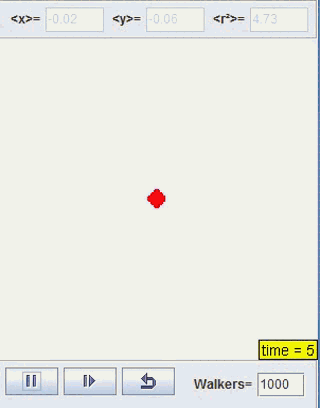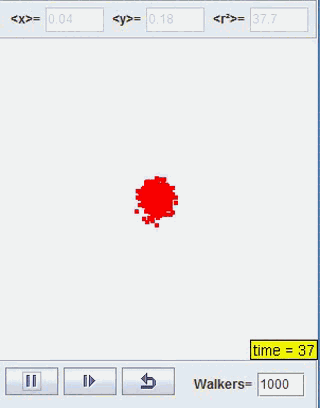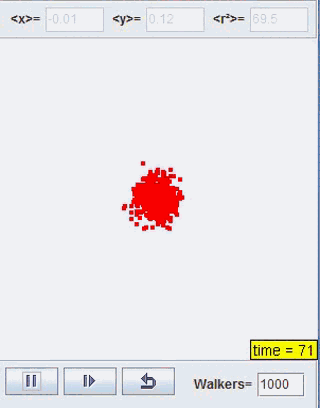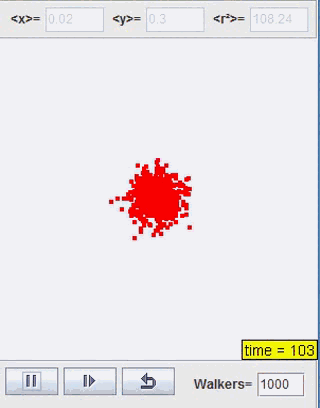
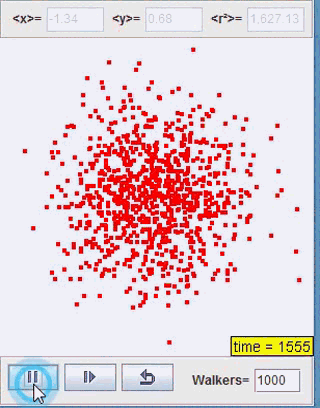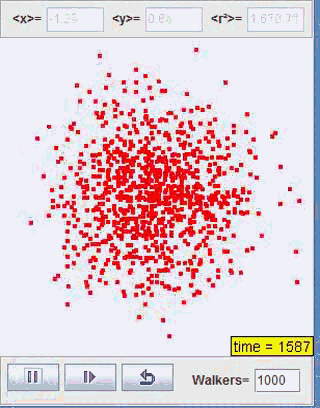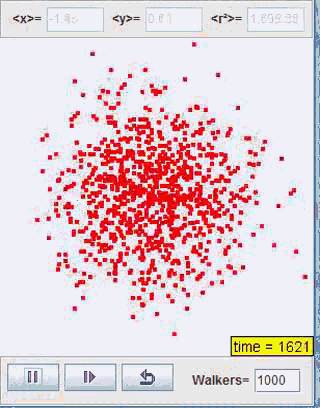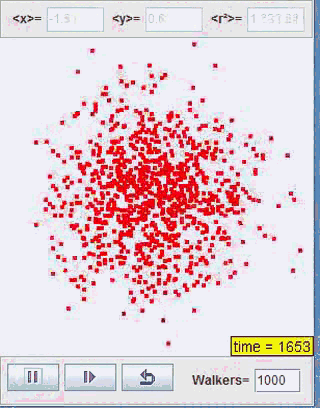
　　熵的变化：
　　
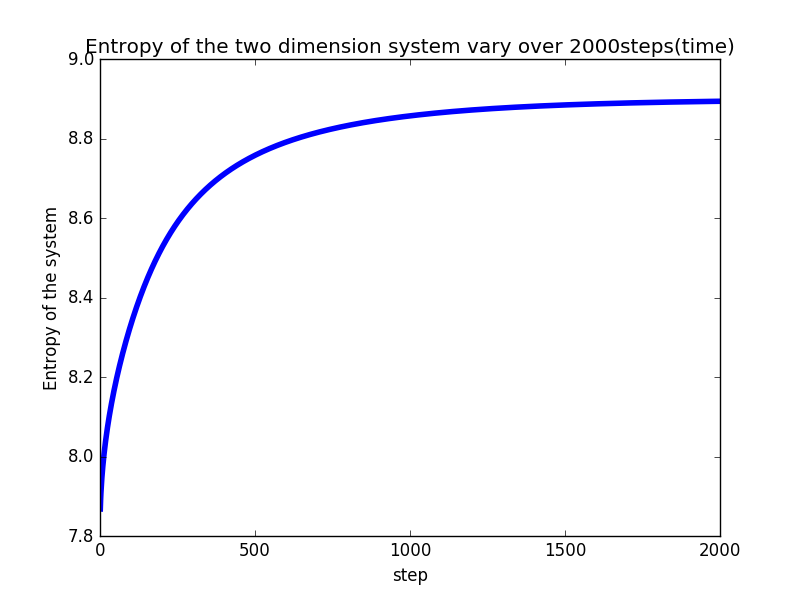
　　由此可见，整个过程的熵是增加的，而这也反映了时间的方向。且随着时间增大，熵的值的增长速度降低，最终它会收敛到一个定值。
　　

参考文献

1. 计算物理 Nicholas J.Giordano, Hisao Nakanishi 清华大学出版社
2. Wikipedia Random system
3. Wikipedia Diffusion