@zy-0815
2017-12-20T13:46:15.000000Z
字数 6936
阅读 1699
计算物理第九次作业
计算物理
摘要
我们将探究碰撞反射问题,研究小球在方形界面、球形界面中的运动轨迹,及其影响因素,同时本次作业就3.30题进行探究和解答
背景
反射是在日常生活中较为常见的一种现象,无论是光的反射亦或是台球碰撞后的反弹,其遵循的基本规律都是反射定律,即反射角等于入射角。则对于速度,有如下的关系式:
同时我们知道,不同的边界条件将对反射的运动轨迹造成不同的影响,若为直线边界,则如图:
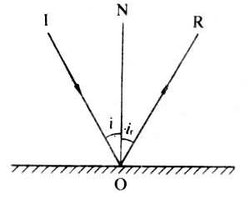
若为弧形边界,则类似Figure 3.19,初射角的分析将比之前略复杂:
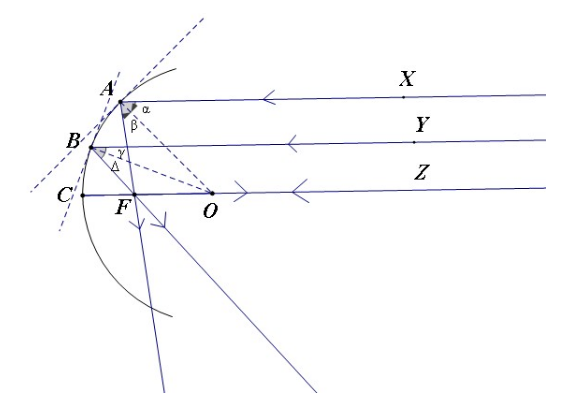
当我们将圆形边界沿直径切开,并拉开一段距离(称之为 Stadium Billiard),情况会复杂很多:
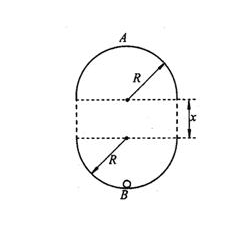
这里我们将研究不同边界条件对小球运动的影响
正文
1. 小球在方形边界中的运动
import pylab as plimport mathclass Billiard_Program :def __init__(self,i=0,initial_theta=math.pi/6,initial_velocity=1,total_time=500,\initial_x=0.2,initial_y=0,time_step=0.01):self.theta=initial_thetaself.v=initial_velocityself.v_x=[self.v*math.cos(self.theta)]self.v_y=[self.v*math.sin(self.theta)]self.x=[initial_x]self.y=[initial_y]self.time=total_timeself.dt=time_stepself.t=[0]def run(self):_time=0while(_time<self.time):self.x.append(self.x[-1]+self.v_x[-1]*self.dt)self.y.append(self.y[-1]+self.v_y[-1]*self.dt)if(self.x[-1]>1):self.x[-1]=self.x[-2]self.y[-1]=self.y[-2]while(1):self.x.append(self.x[-1]+self.v_x[-1]*self.dt*0.01)self.y.append(self.y[-1]+self.v_y[-1]*self.dt*0.01)if(self.x[-1]>1):self.v_x.append(-self.v_x[-1])breakif(self.x[-1]<-1):self.x[-1]=self.x[-2]self.y[-1]=self.y[-2]while(1):self.x.append(self.x[-1]+self.v_x[-1]*self.dt*0.01)self.y.append(self.y[-1]+self.v_y[-1]*self.dt*0.01)if(self.x[-1]<-1):self.v_x.append(-self.v_x[-1])breakif(self.y[-1]>1):self.x[-1]=self.x[-2]self.y[-1]=self.y[-2]while(1):self.x.append(self.x[-1]+self.v_x[-1]*self.dt*0.01)self.y.append(self.y[-1]+self.v_y[-1]*self.dt*0.01)if(self.y[-1]>1):self.v_y.append(-self.v_y[-1])breakif(self.y[-1]<-1):self.x[-1]=self.x[-2]self.y[-1]=self.y[-2]while(1):self.x.append(self.x[-1]+self.v_x[-1]*self.dt*0.01)self.y.append(self.y[-1]+self.v_y[-1]*self.dt*0.01)if(self.y[-1]<-1):self.v_y.append(-self.v_y[-1])breakself.t.append(_time)_time += self.dtdef show_results(self):pl.plot(self.x,self.y)pl.title('Billiard Program with $\\theta$=$\pi$/6')pl.xlabel('x')pl.ylabel('y')pl.xlim(-1,1)pl.ylim(-1,1)pl.legend()pl.show()a = Billiard_Program()a.run()a.show_results()
2. 小球在圆形界面中的运动
import pylab as plimport mathclass Billiard_Program :def __init__(self,i=0,initial_theta=math.pi/6,initial_velocity=1,total_time=80,\initial_x=0.2,initial_y=0,time_step=0.01):self.theta=[initial_theta]self.v=[initial_velocity]self.x=[initial_x]self.y=[initial_y]self.time=total_timeself.dt=time_stepself.t=[0]self.phi=[]self.v_x=[self.v[-1]*math.cos(self.theta[-1])]self.v_y=[self.v[-1]*math.sin(self.theta[-1])]def run(self):_time=0a=0.1r=1while(_time<self.time):self.x.append(self.x[-1]+self.v_x[-1]*self.dt)self.y.append(self.y[-1]+self.v_y[-1]*self.dt)if(self.y[-1]<-a*r and (pow(self.x[-1],2)+pow(self.y[-1]+a*r,2))>pow(r,2)):self.x[-1]=self.x[-2]self.y[-1]=self.y[-2]while(1):self.x.append(self.x[-1]+self.v_x[-1]*self.dt*0.01)self.y.append(self.y[-1]+self.v_y[-1]*self.dt*0.01)if(pow(self.x[-1],2)+pow(self.y[-1]+a*r,2)>pow(r,2)):cos_theta=self.x[-1]/rsin_theta=(self.y[-1]+a*r)/rvi_prependicular_x=abs(self.v_x[-1]*cos_theta+self.v_y[-1]*sin_theta)*cos_thetavi_prependicular_y=abs(self.v_x[-1]*cos_theta+self.v_y[-1]*sin_theta)*sin_thetavi_parallel_x=self.v_x[-1]-abs(self.v_x[-1]*cos_theta+self.v_y[-1]*sin_theta)*cos_thetavi_parallel_y=self.v_y[-1]-abs(self.v_x[-1]*cos_theta+self.v_y[-1]*sin_theta)*sin_thetavf_parallel_x=vi_parallel_xvf_parallel_y=vi_parallel_yvf_prependicular_x=-vi_prependicular_xvf_prependicular_y=-vi_prependicular_yvf_x=vf_parallel_x+vf_prependicular_xvf_y=vf_parallel_y+vf_prependicular_yself.v_x.append(vf_x)self.v_y.append(vf_y)breakif(self.y[-1]>a*r and (pow(self.x[-1],2)+pow(self.y[-1]-a*r,2))>pow(r,2)):self.x[-1]=self.x[-2]self.y[-1]=self.y[-2]while(1):self.x.append(self.x[-1]+self.v_x[-1]*self.dt*0.01)self.y.append(self.y[-1]+self.v_y[-1]*self.dt*0.01)if(pow(self.x[-1],2)+pow(self.y[-1]-a*r,2)>pow(r,2)):cos_theta=self.x[-1]/rsin_theta=(self.y[-1]-a*r)/rvi_prependicular_x=abs(self.v_x[-1]*cos_theta+self.v_y[-1]*sin_theta)*cos_thetavi_prependicular_y=abs(self.v_x[-1]*cos_theta+self.v_y[-1]*sin_theta)*sin_thetavi_parallel_x=self.v_x[-1]-abs(self.v_x[-1]*cos_theta+self.v_y[-1]*sin_theta)*cos_thetavi_parallel_y=self.v_y[-1]-abs(self.v_x[-1]*cos_theta+self.v_y[-1]*sin_theta)*sin_thetavf_parallel_x=vi_parallel_xvf_parallel_y=vi_parallel_yvf_prependicular_x=-vi_prependicular_xvf_prependicular_y=-vi_prependicular_yvf_x=vf_parallel_x+vf_prependicular_xvf_y=vf_parallel_y+vf_prependicular_yself.v_x.append(vf_x)self.v_y.append(vf_y)breakif(-a<self.y[-1]<a and self.x[-1]>1):self.x[-1]=self.x[-2]self.y[-1]=self.y[-2]while(1):self.x.append(self.x[-1]+self.v_x[-1]*self.dt*0.01)self.y.append(self.y[-1]+self.v_y[-1]*self.dt*0.01)if(self.x[-1]>1):self.v_x.append(-self.v_x[-1])breakif(-a<self.y[-1]<a and self.x[-1]<-1):self.x[-1]=self.x[-2]self.y[-1]=self.y[-2]while(1):self.x.append(self.x[-1]+self.v_x[-1]*self.dt*0.01)self.y.append(self.y[-1]+self.v_y[-1]*self.dt*0.01)if(self.x[-1]<-1):self.v_x.append(-self.v_x[-1])breakself.t.append(_time)_time += self.dtdef show_results(self):pl.plot(self.x,self.y)pl.title('Circular stadium with $\\theta$=$\pi$/6')pl.xlabel('x')pl.ylabel('y')pl.xlim(-1.2,1.2)pl.ylim(-1.2,1.2)pl.legend()pl.show()a = Billiard_Program()a.run()a.show_results()
结论
1. 小球在方形界面中的运动
1.1 初始角度的影响
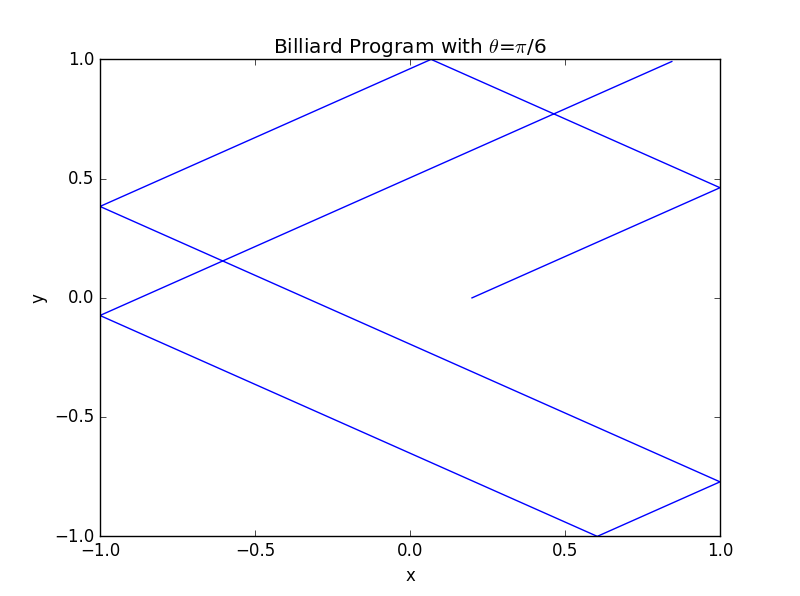
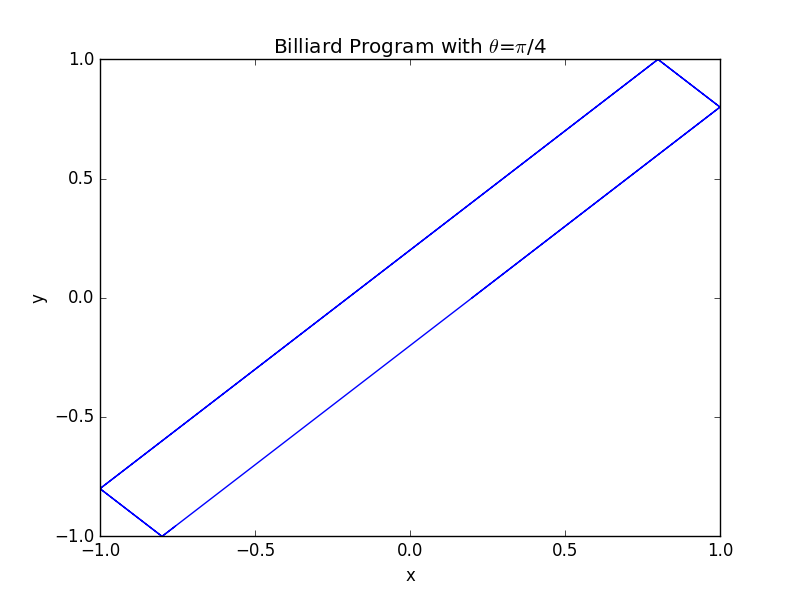
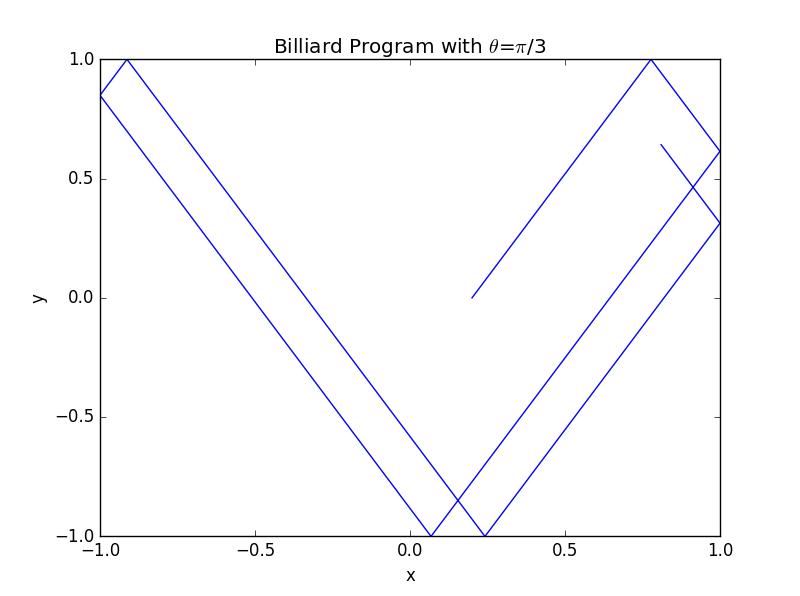
1.2 以 为基础,增长程序运行时间
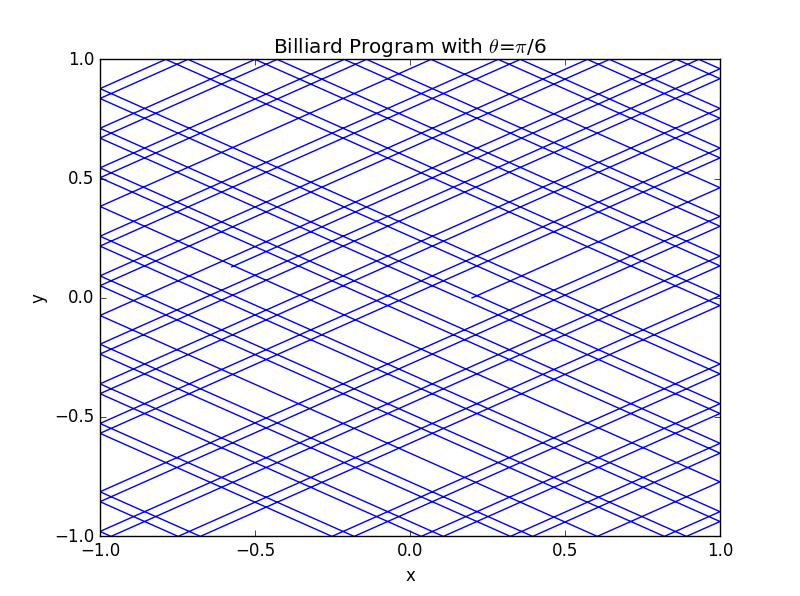
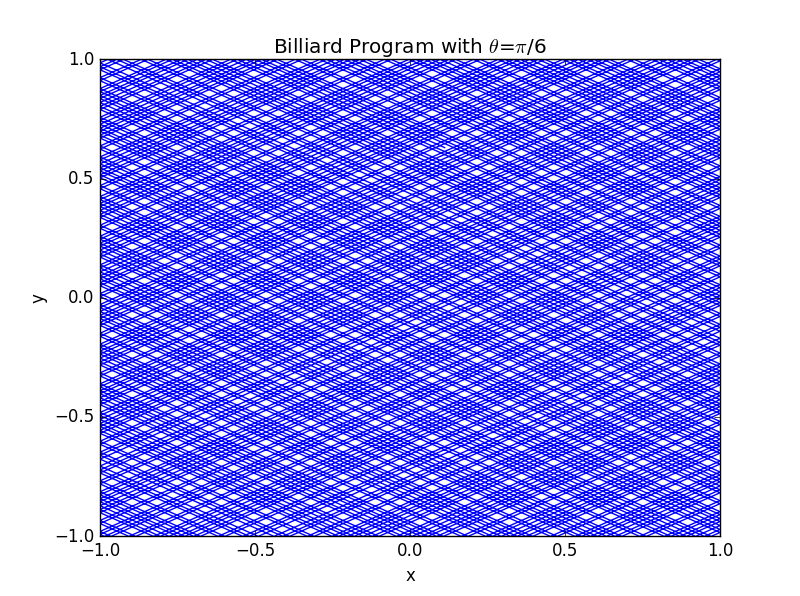
可见若时间足够长,轨迹将铺满整个平面
1.3 相空间
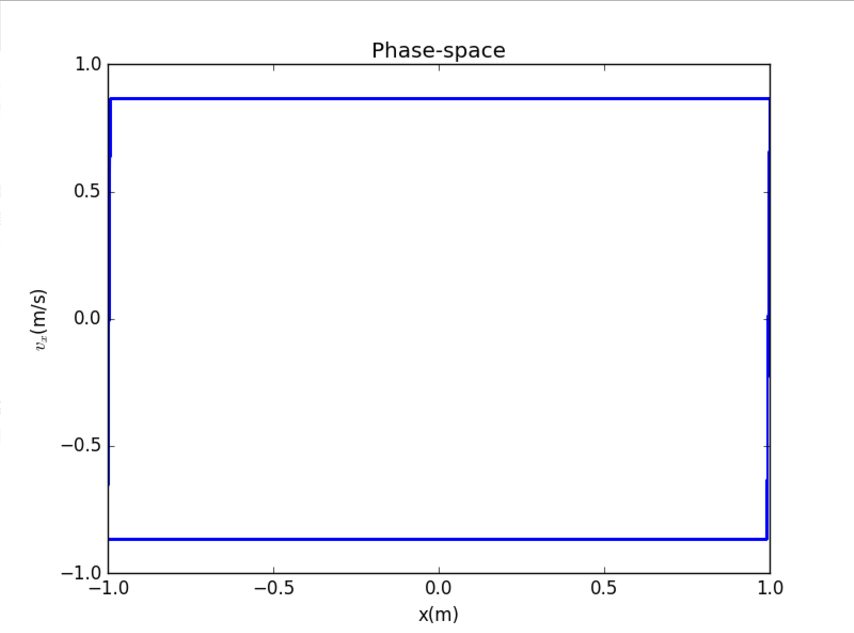
可见小球的速度在两确定值间变化
2. 圆形边界
2.1 正圆边界
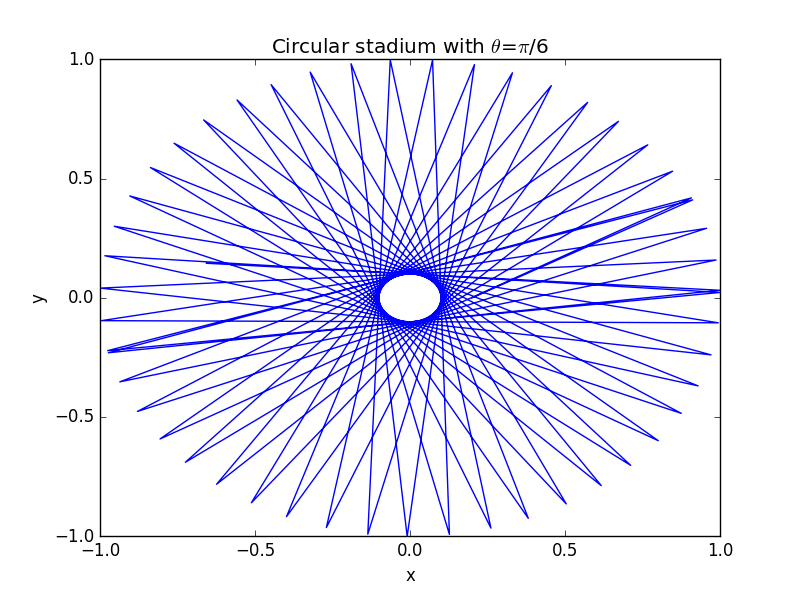
2.2 Stadium Billiard
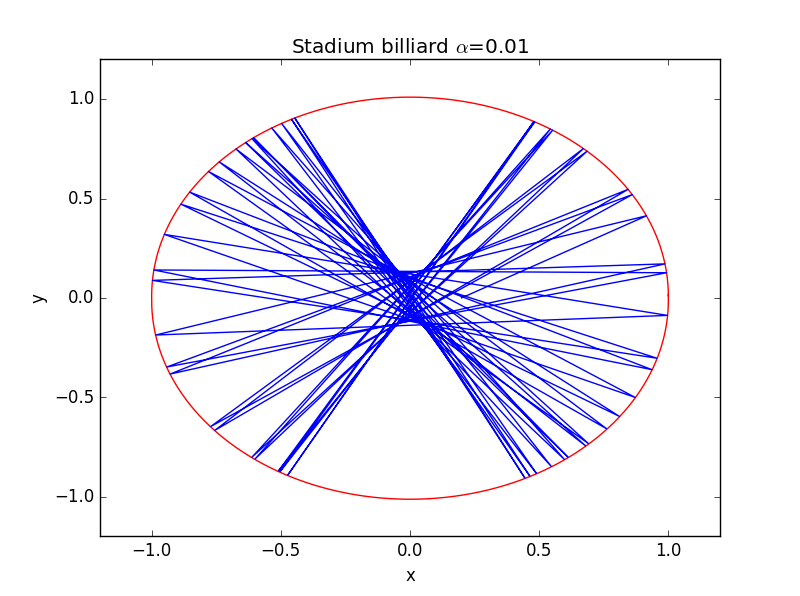
改变的取值

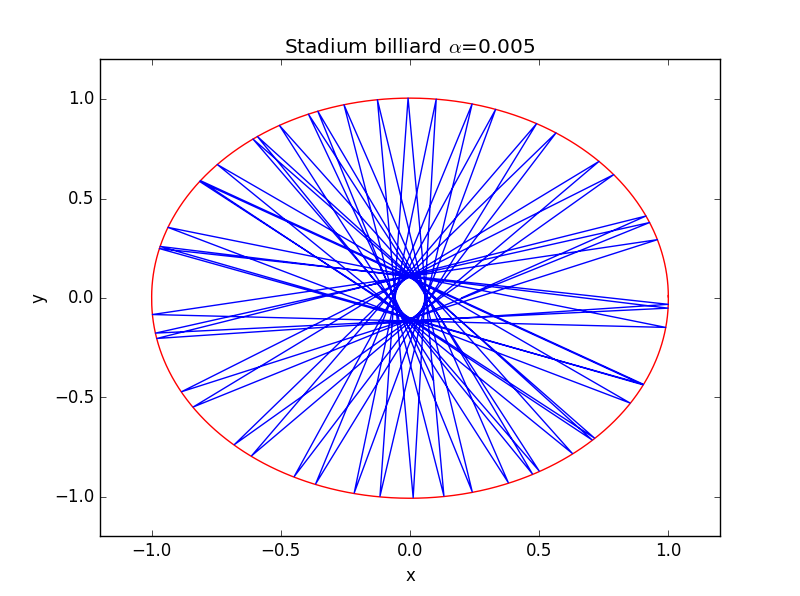
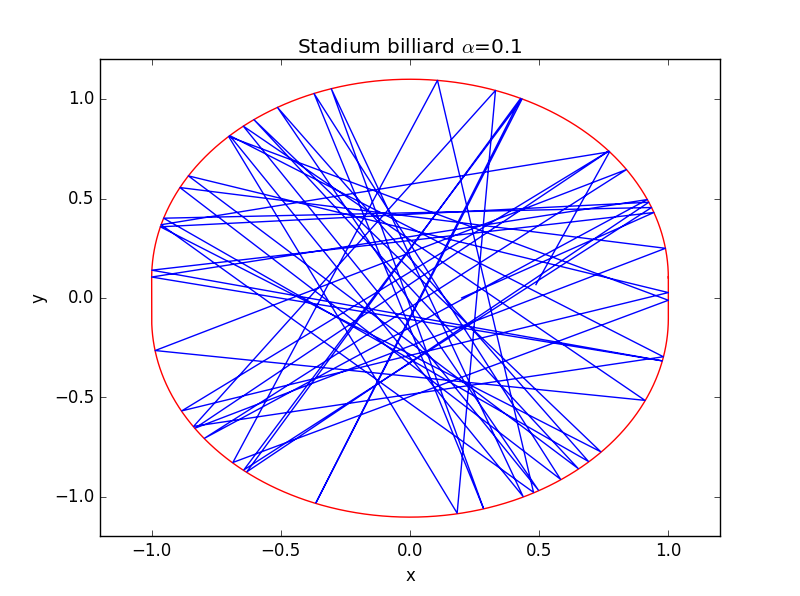
可见时整个运动轨迹已发生了巨大改变,若我们将改至足够大,使之完全成为“体育场形”则有:
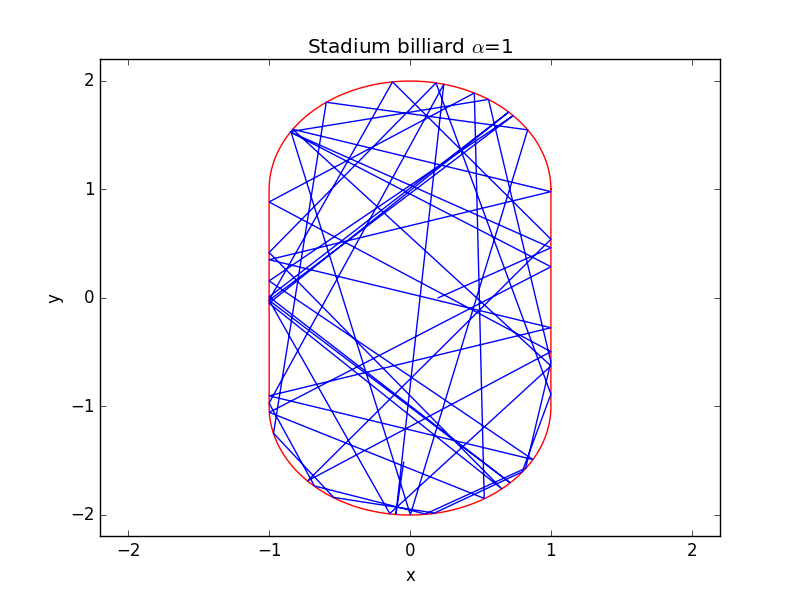
2.3 相空间
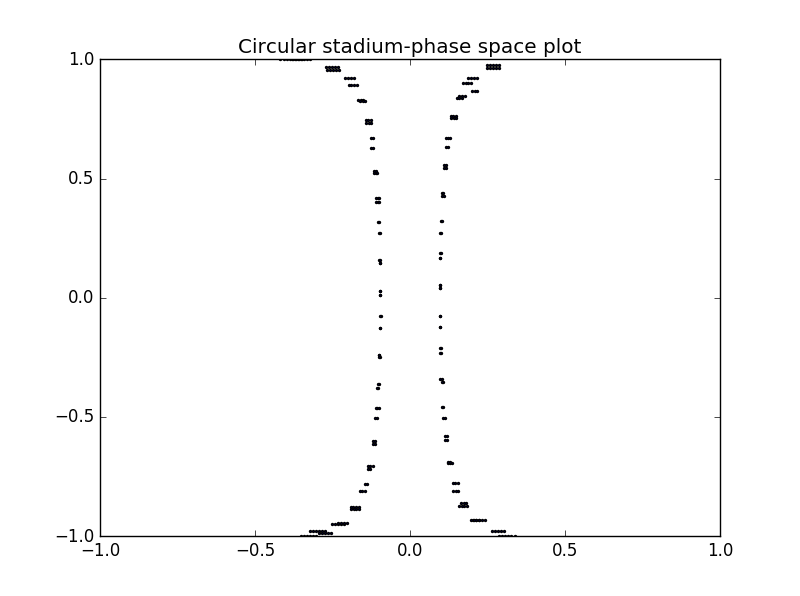
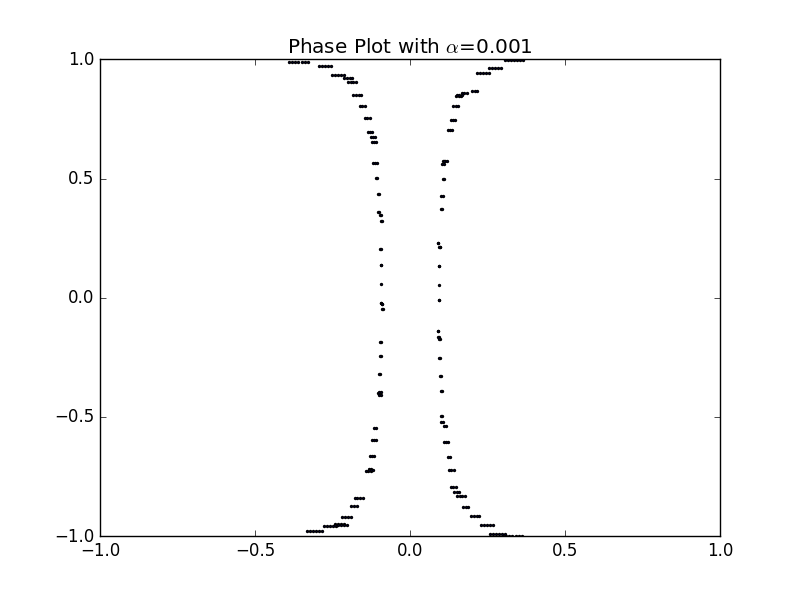
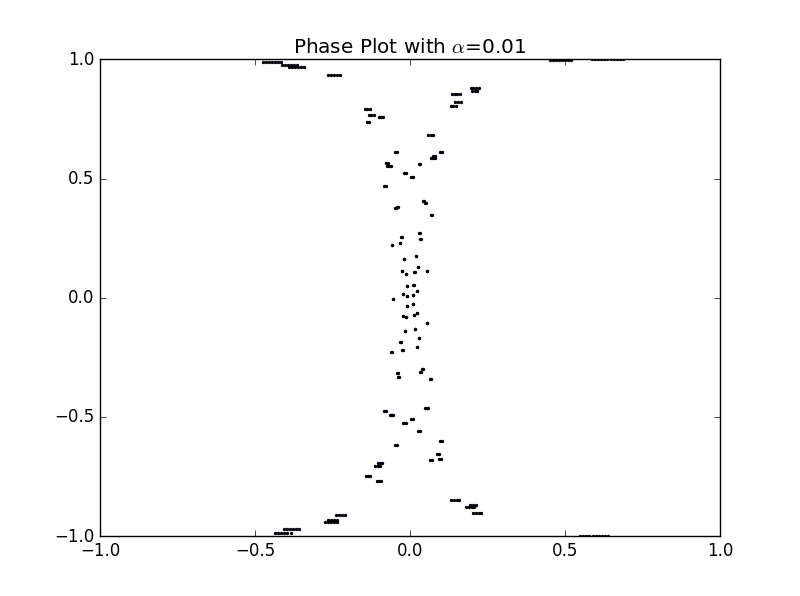
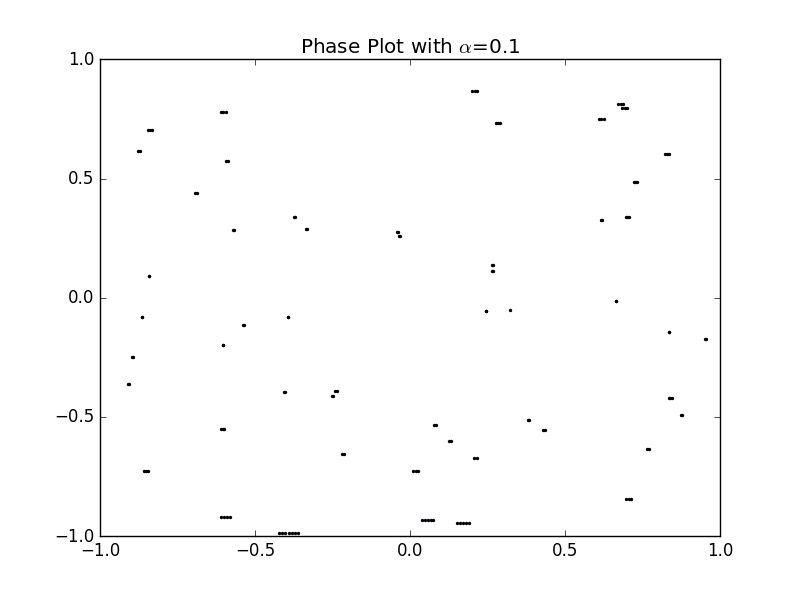
当时,轨迹已布满整个相空间,标志着运动以完全混乱
3 Problem 3.30
我们同时释放两个小球,他们有微小的初始位置差别,研究他们的运动,则有如下图像,此处设初始位置x相差0.001
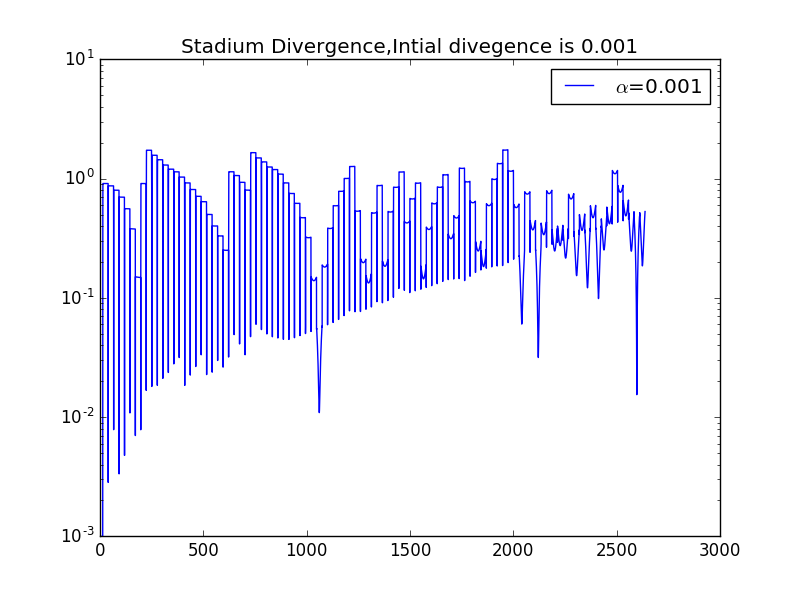
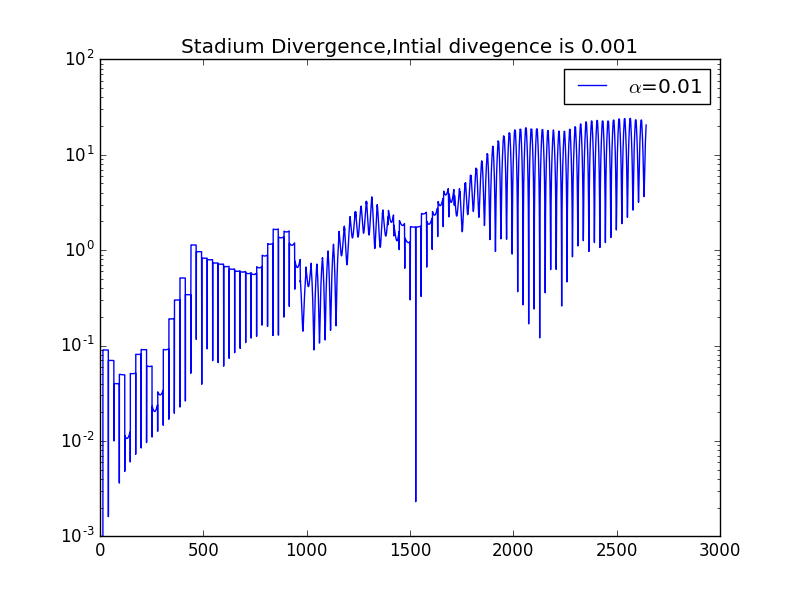
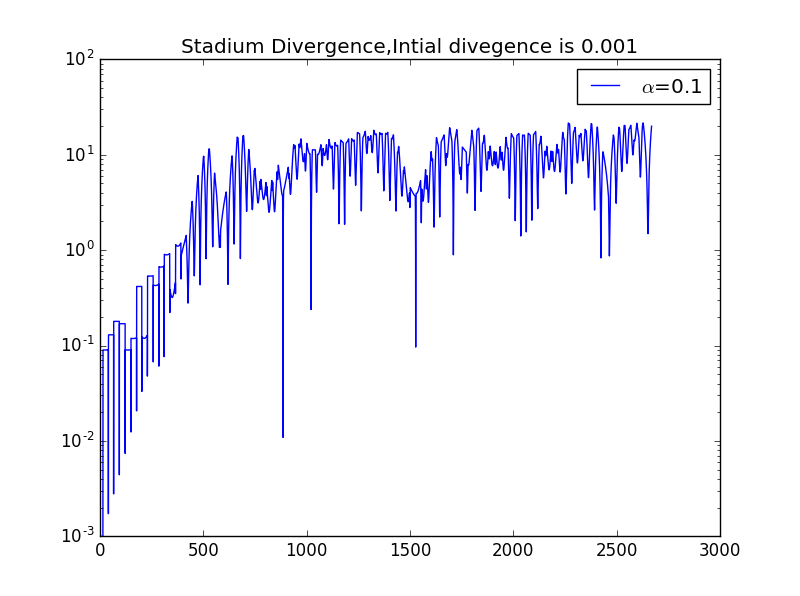
反思
1. 精度问题
为了提高小球在遇到边界时对边界的判断精度,我们采取如下算法,即超过边界时后退一步,再以更小步长前进,这一部分在程序中的表现如下:
if(self.x[-1]>1):self.x[-1]=self.x[-2]self.y[-1]=self.y[-2]while(1):self.x.append(self.x[-1]+self.v_x[-1]*self.dt*0.01)self.y.append(self.y[-1]+self.v_y[-1]*self.dt*0.01)if(self.x[-1]>1):self.v_x.append(-self.v_x[-1])break
当然,对于该问题同样可以一开始就采用小步长,但这样无疑会加大计算量,当程序越来越长时会严重拖慢计算速度,在本次作业的最终程序面前,我的计算机已经出现了卡顿,不得不缩减步长,若一开始就采用高精度,则结果一定是大大拖慢程序进程,因此对这种算法不予考虑
同时,我们可以检验程序的精度,即将出射点改为(0,0),出射角为,若精度较高,则仅有一条直线,如图:

亦或进行局部放大,以球形边界为例(注意由于放大后出现失真,表现的似乎不满足反射定律):
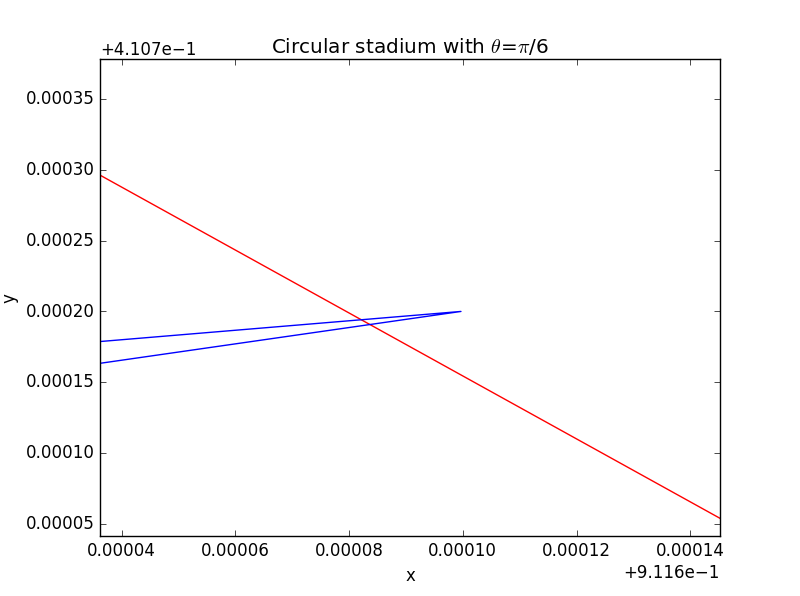
综上可见我们的精度还是比较高的
2. 程序报错
在编写过程中常会弹出此类错误:

此类错误非常容易出现,而产生的原因也很简单,是由于两变量字符串内所含元素的数量不相等,因此当给一个元素添加新的元素时,要注意另一坐标轴变量元素的添加
3. 进一步的探讨
其实我们还可以使用Vpython进行编写,从而更直观的看到小球的运动情况,
程序如下:
from visual import *side = 4.0thk = 0.3s2 = 2*side - thks3 = 2*side + thkwallR = box (pos=( side, 0, 0), size=(thk, s2, s3), color = color.red)wallL = box (pos=(-side, 0, 0), size=(thk, s2, s3), color = color.red)wallB = box (pos=(0, -side, 0), size=(s3, thk, s3), color = color.blue)wallT = box (pos=(0, side, 0), size=(s3, thk, s3), color = color.blue)ball = sphere(pos=(0.2,0,0), color=color.red, radius = 0.4, make_trail=True, retain=200)ball.trail_object.radius = 0.05ball.v = vector(0.5,0.3,0)side = side - thk*0.5 - ball.radiusdt = 0.5t=0.0while True:rate(100)t = t + dtball.pos = ball.pos + ball.v*dtif not (side > ball.x > -side):ball.v.x = -ball.v.xif not (side > ball.y > -side):ball.v.y = -ball.v.y
结果如下图所示:

当然,我们也可让小球在三面上碰撞
鸣谢
张梓桐同学帮助纠正了程序在反射运动部分的小bug
