@zy-0815
2016-10-18T03:24:27.000000Z
字数 2668
阅读 6874
利用Matlab可视化功能实现微分方程求解行星运动轨迹
1.背景
在物理学璀璨的发展史上,物理学家花了很长时间研究我们头顶浩瀚的星空,试图探究星星的运行模式,以及地球自身的运动模式。其中不乏像亚里士多德,伽利略,布鲁诺,开普勒,第谷,牛顿等物理大家参与其中。他们对与行星的研究在经典物理学的发展史上刻下了不可磨灭的痕迹。随着牛顿与莱布尼兹的微积分学的创立,以及之后牛顿提出的牛顿三定律的问世,为物理学家研究行星的运动轨迹打下了坚实的理论基础。本文正是以牛顿第二定律的微分方程为基础,利用数学工具Matlab及其优越的可视化功能实现前人花费数千年时间所研究的行星轨道运动问题,并将其以生动直观的轨迹图表示出来。
2.程序组成
本Matlab程序有3个子M文件组成分别为: planet.m, plode.m, Planet_Orbit.m组成。其中,planet.m用以实现绘图功能,plode.m为核心文件,包含了运动的微分方程,Planet_Orbit.m用以时间图形的界面化操作。另外由一个图形界面文件Planet_Orbit.fig组成。
3.研究方法
根据牛顿提出的牛顿第二定律方程:
其中 为物体所受到的合力, 为物体的加速度。将其运用到极坐标系中,并赋予力 以形式 ,得到物体运动的轨道微分方程:
4.程序内容及M文件界面
4.1 Plode.m文件
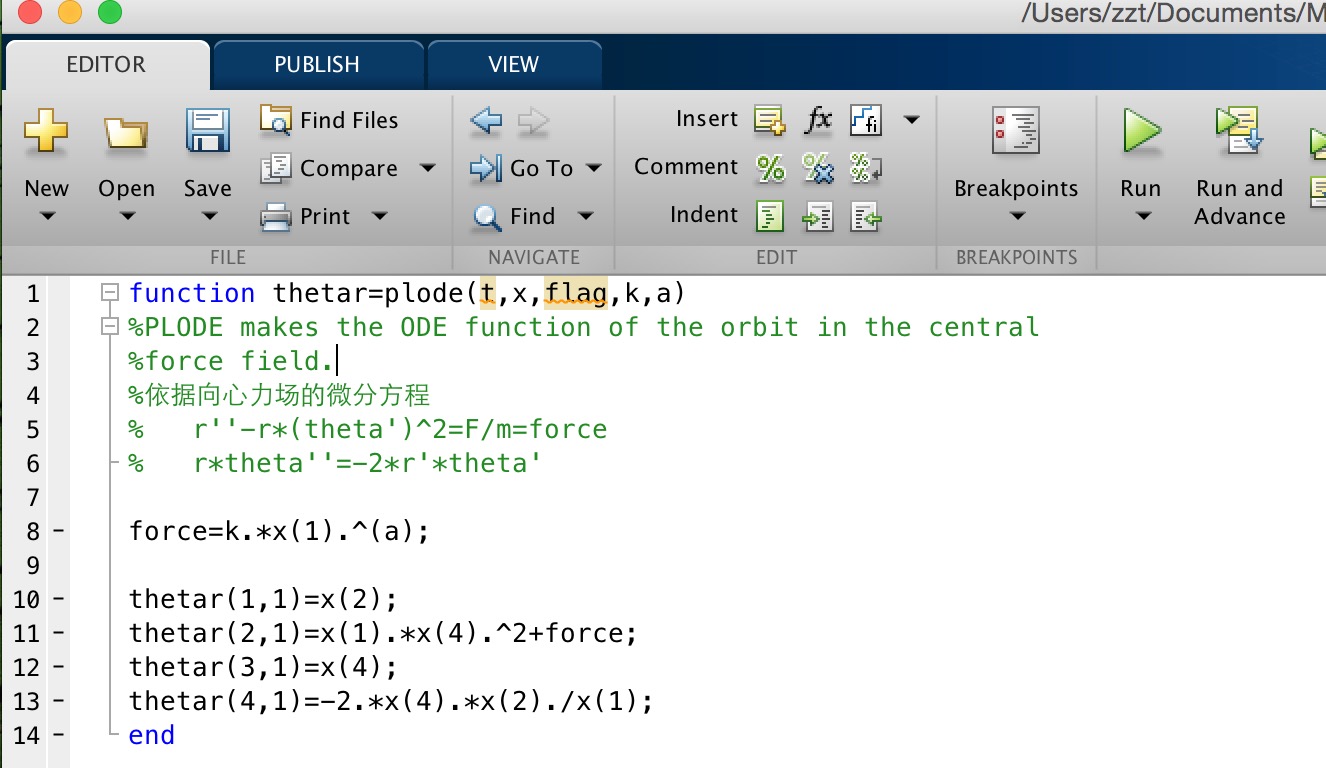
利用上述两式进行本程序的核心M文件plode.m:
function thetar=plode(t,x,flag,k,a)%PLODE makes the ODE function of the orbit in the central%force field.%依据向心力场的微分方程% r''-r*(theta')^2=F/m=force% r*theta''=-2*r'*theta'force=k.*x(1).^(a);thetar(1,1)=x(2);thetar(2,1)=x(1).*x(4).^2+force;thetar(3,1)=x(4);thetar(4,1)=-2.*x(4).*x(2)./x(1);end
定义变量:
t ---time range,时间区间为[0,t]
x ---x是一个4x1的列向量,参数分别为
r ----inital r,初始时刻的轨道半径
r1---initial r',初始时刻的轨道径向速度
theta --initial angle,初始时刻的角度
theta1 --initial theta',初始时刻的角速度
flag --对微分方程添加补充功能的参数(类型为structure,用odeset来定义)
force --向心力, force=F/m=k*r^a,其中F为真实力,m为行星质量
k --向心力的系数
a --index of r
其在M文件运行窗的截图如下:
4.2 planet.m文件
此文件用于对处在中心立场中的行星进行绘图功能的实现。
函数Planet接受行星运动的初始值,运动的时间范围,以及中心立场的不同形式
定义变量:
T --time range,时间区间为[0,T]
r --inital r,初始时刻的轨道半径
r1 --initial r',初始时刻的轨道径向速度
theta --initial angle,初始时刻的角度
theta1 --initial theta',初始时刻的角速度
向心力为: force=F/m=k*r^a,其中F为真实力,m为行星质量
k --向心力的系数
a --r的指数
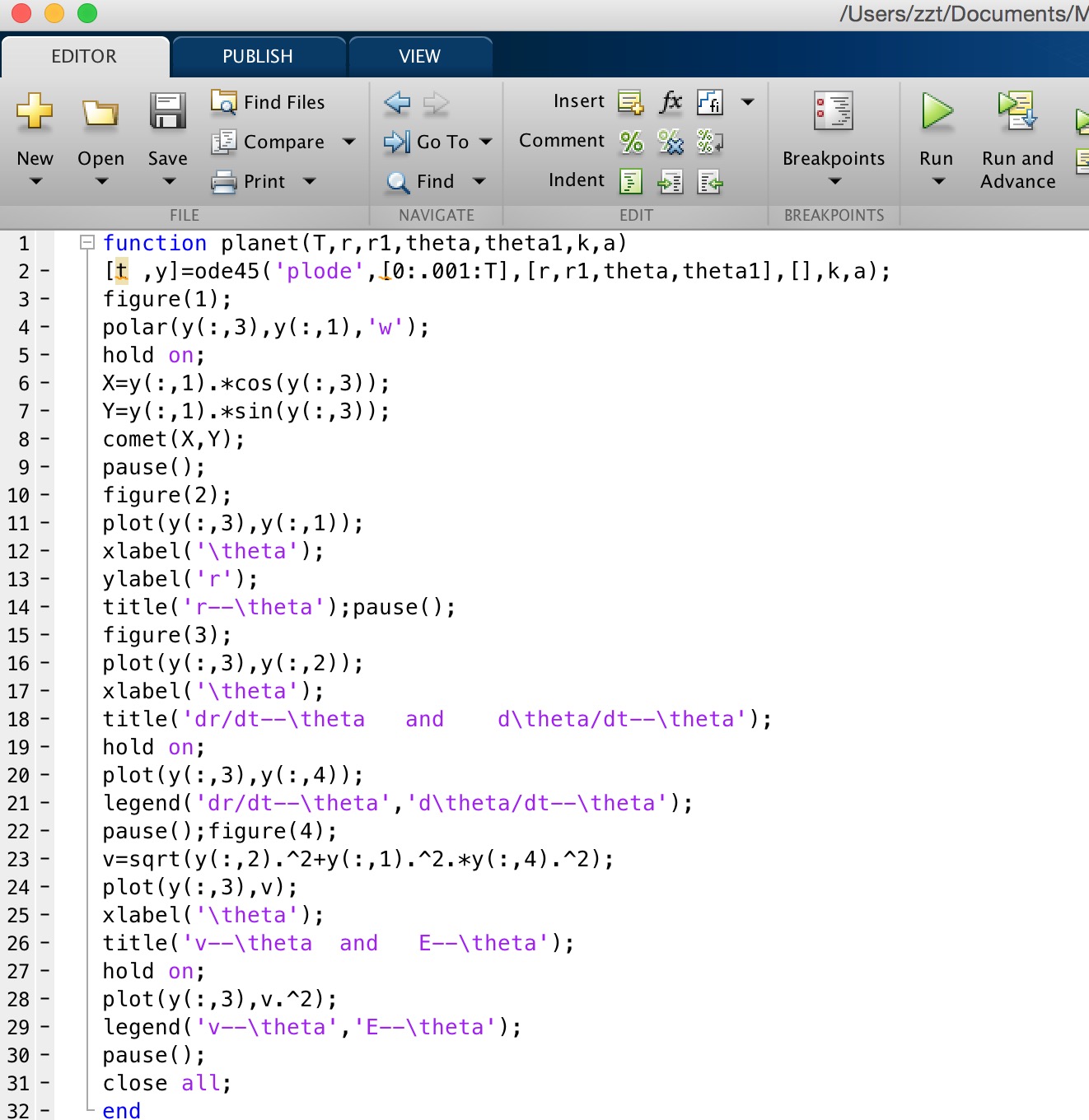
function planet(T,r,r1,theta,theta1,k,a)[t ,y]=ode45('plode',[0:.001:T],[r,r1,theta,theta1],[],k,a);figure(1);polar(y(:,3),y(:,1),'w');hold on;X=y(:,1).*cos(y(:,3));Y=y(:,1).*sin(y(:,3));comet(X,Y);pause();figure(2);plot(y(:,3),y(:,1));xlabel('\theta');ylabel('r');title('r--\theta');pause();figure(3);plot(y(:,3),y(:,2));xlabel('\theta');title('dr/dt--\theta and d\theta/dt--\theta');hold on;plot(y(:,3),y(:,4));legend('dr/dt--\theta','d\theta/dt--\theta');pause();figure(4);v=sqrt(y(:,2).^2+y(:,1).^2.*y(:,4).^2);plot(y(:,3),v);xlabel('\theta');title('v--\theta and E--\theta');hold on;plot(y(:,3),v.^2);legend('v--\theta','E--\theta');pause();close all;end
其在M文件运行窗的截图如下:
4.3 Planet_Orbit.m文件
此文件用以实现对行星轨迹运动的动态化以及界面化,由于该程序过于冗长,不将函数体打入文稿,只提供部分其在M文件运行窗的截图(该文件回附于本论文最后):
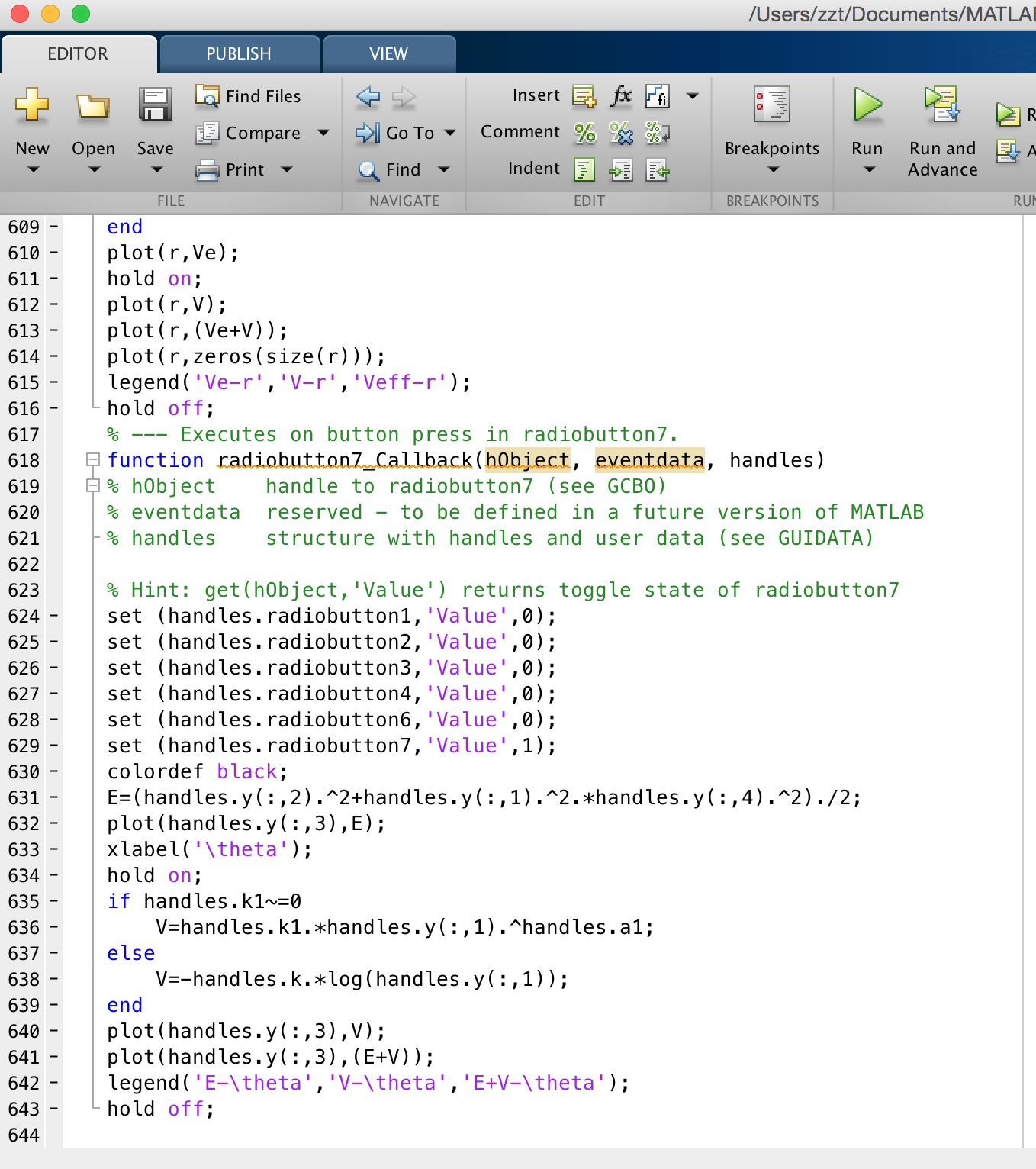
打开后界面如下:
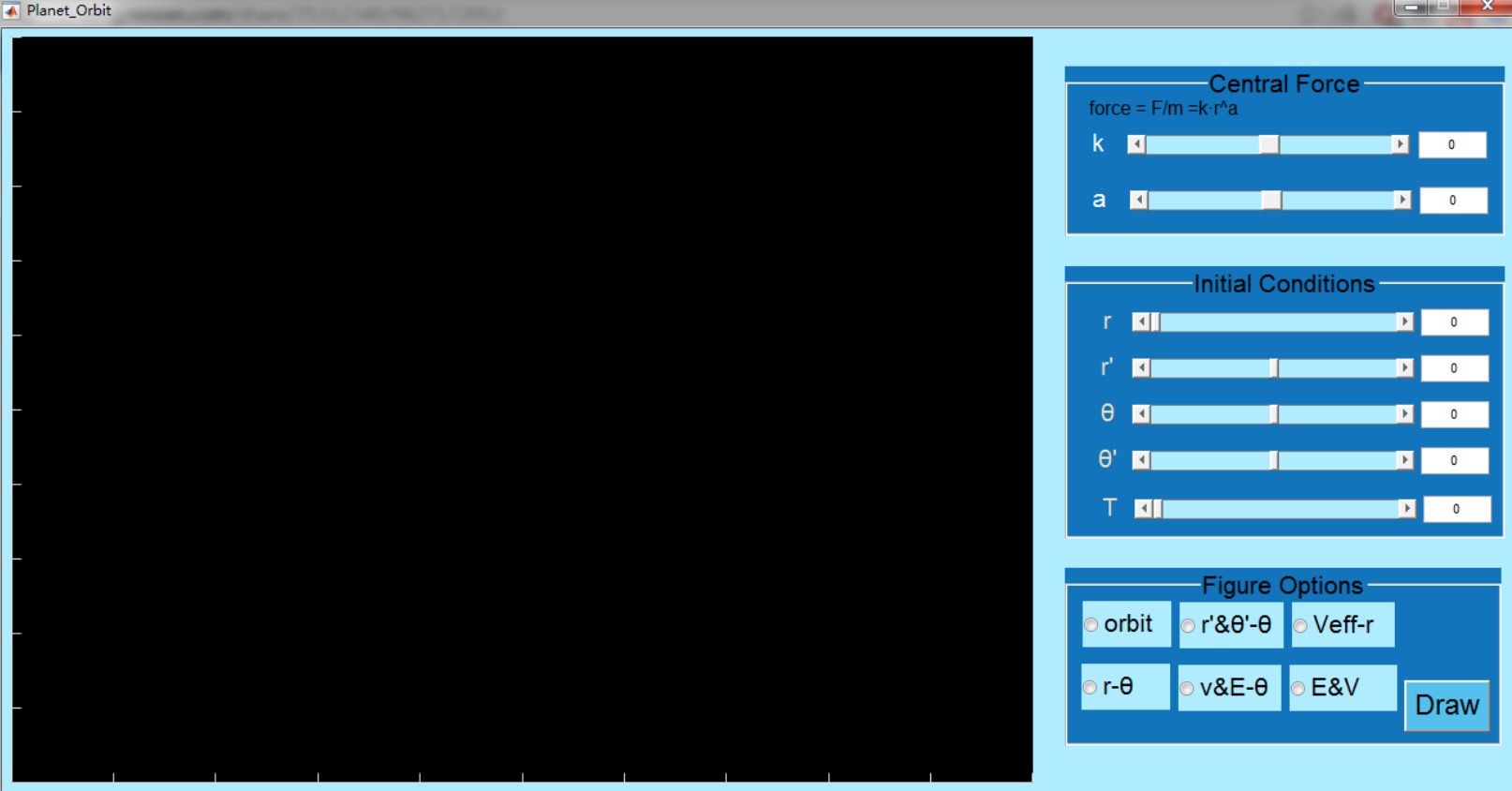
界面的绘图选项说明如下:
1. orbit,画轨道
2. r′&θ′ − θ,画径向速度和角速度随角度的变化
3. Veff −r,画有效势能随r的变化
4. r − θ , 画轨道半径随角度的变化
5. v&E − θ, 画速度和动能随角度的变化
6. V &E , 画势能和动能还有总能量随角度的变化
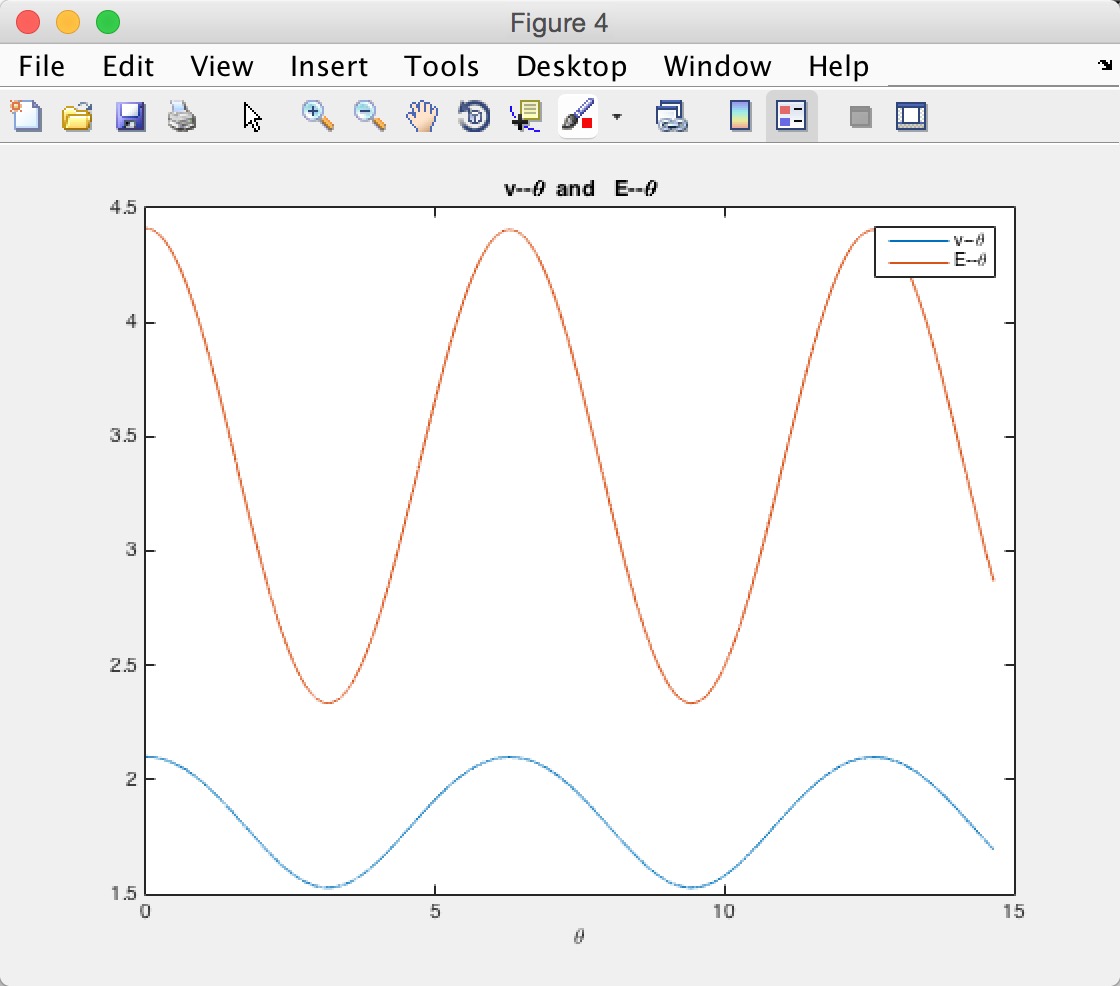
5.运行程序及运行结果
将文件夹中的 planet.m ,Planet_Orbit.m , plode.m,Planet_Orbit.fig 复制粘贴到 MATLAB的当前目录 (Current Folder) 下。在命令窗口(Command Window), 输入 Planet_Orbit,并输入参数。

依次得到四张图,分别为
1.运动轨迹图
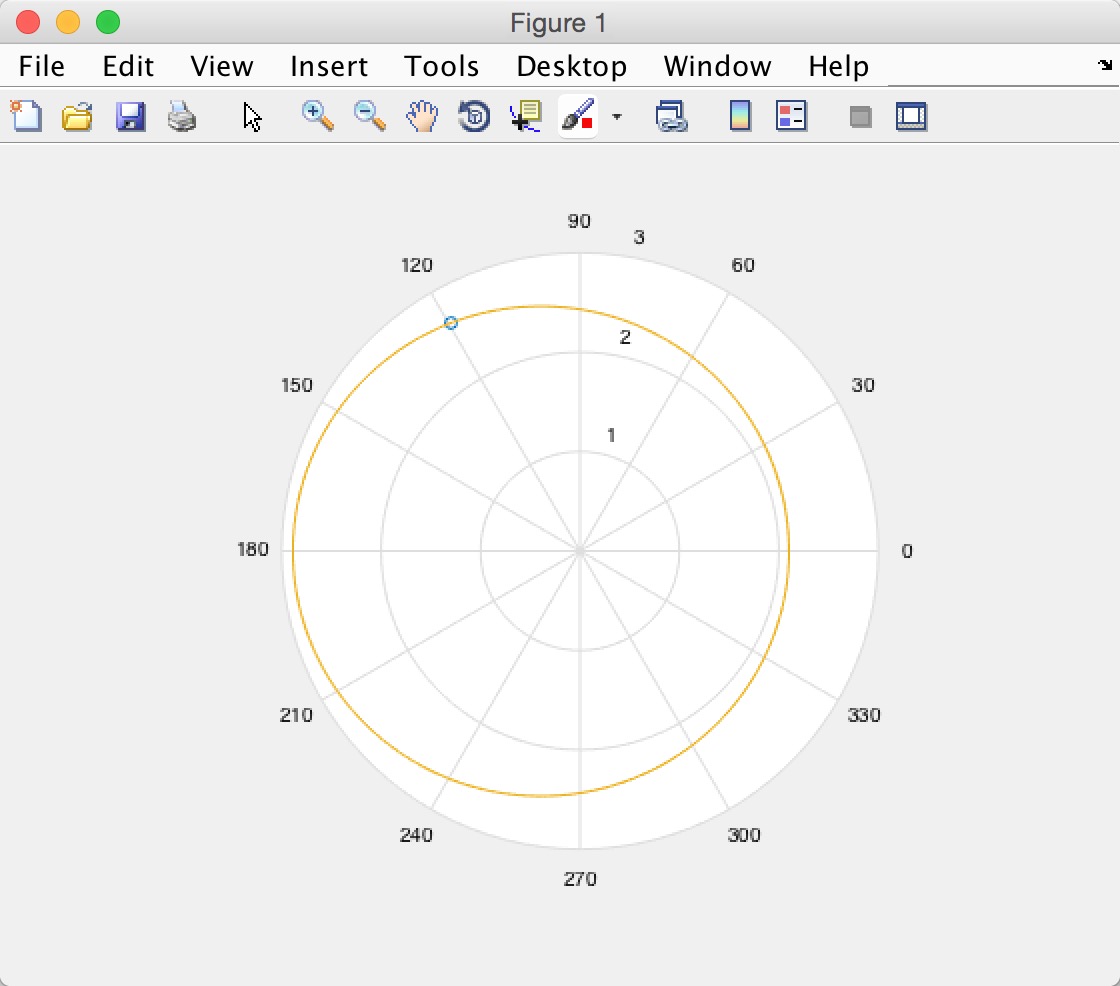
2.与关系图
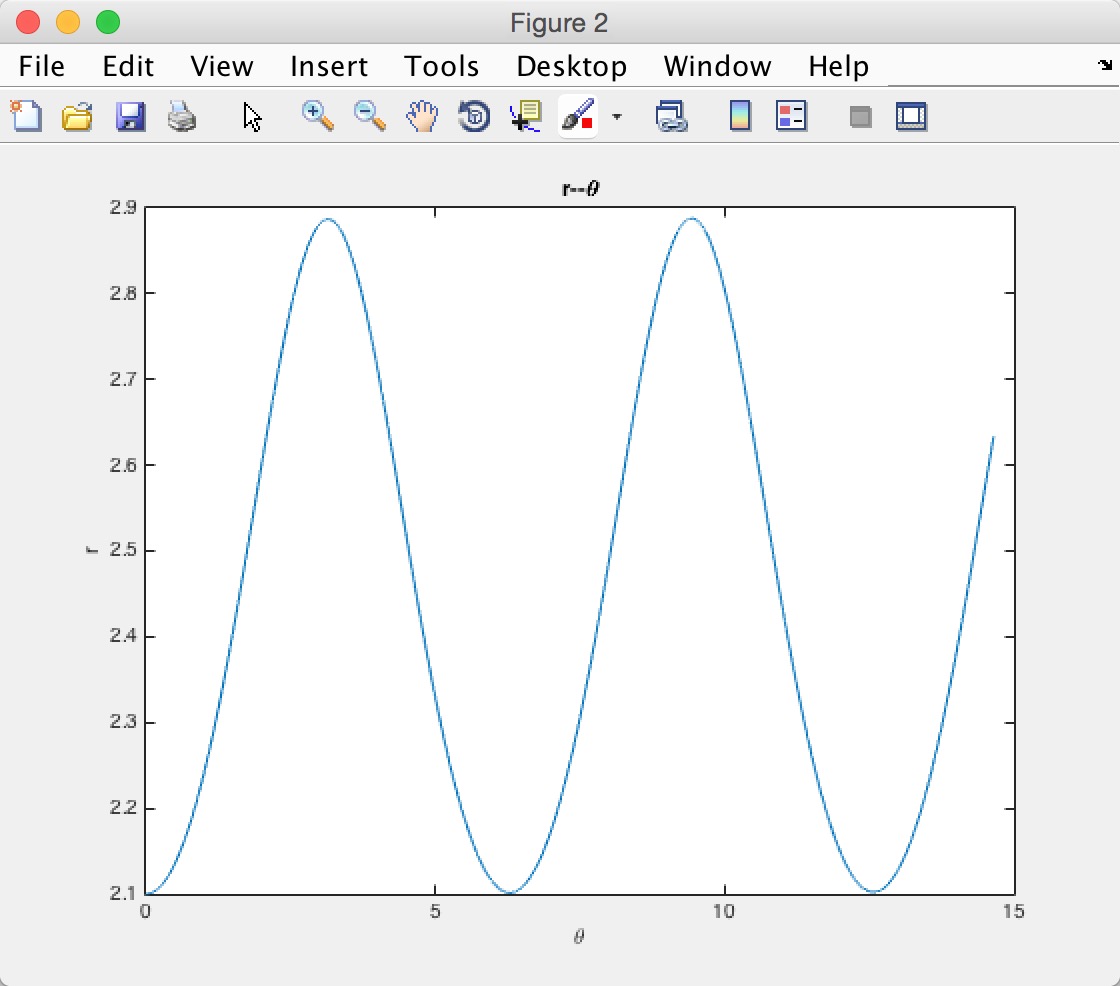
3.&关于图
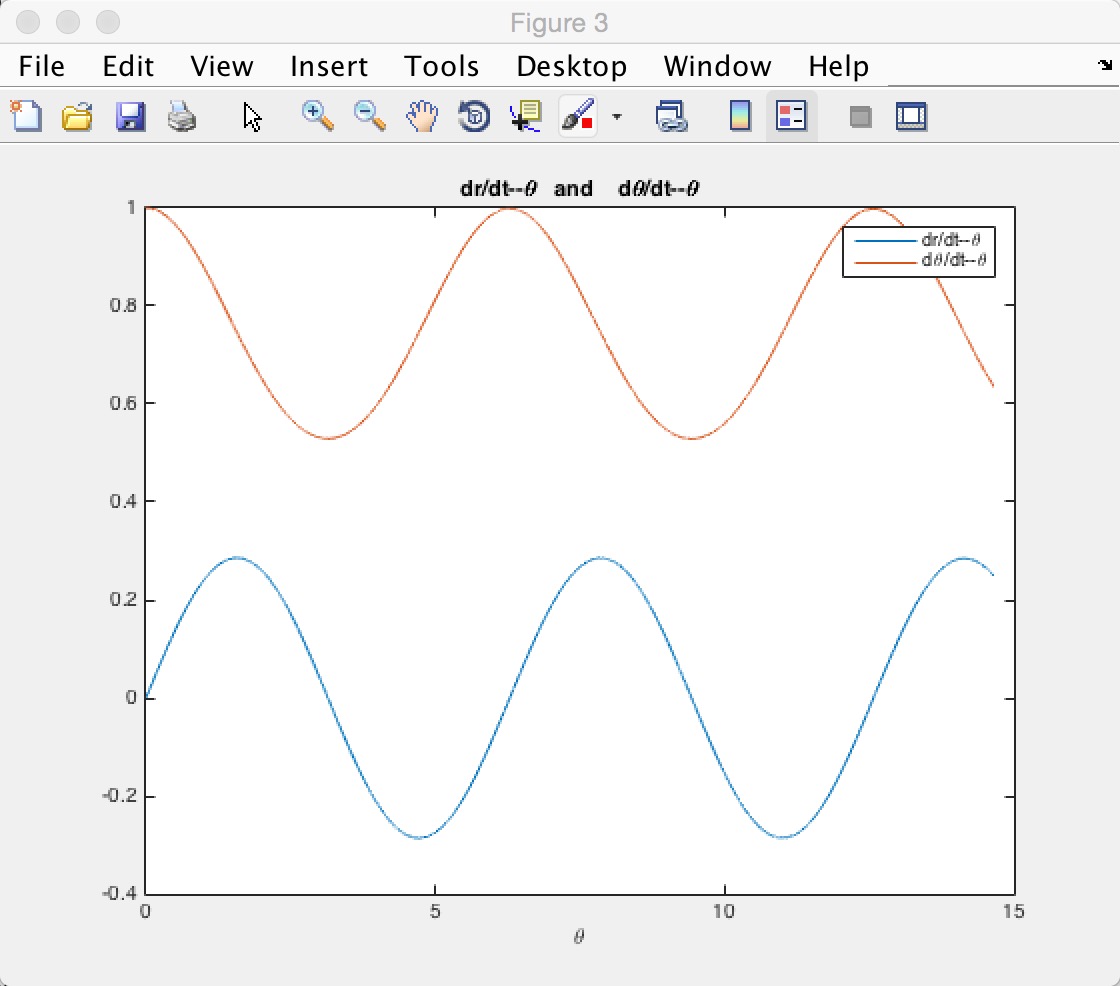
4.动能势能关于图