计算物理第五次作业

计算物理

---

摘要

本次作业主要解决Exercises 2.7的相关问题，即在课本得出Figure 1.4 的基础上，考虑两种模型，即绝热（adiabatic）和等温（isothermal）模型条件下的炮弹运动轨迹，并进一步在引入地表温度变量的情况下，得到更加真实的运动轨迹。

背景介绍

经过上次课程和相关作业的练习，我们初步掌握了欧勒法（Euler Method）的使用。但很显然，在实际应用中，我们之前掌握的欧勒法存在不足，如课本Figure 2.1所示，毕竟是一个理想模型，在解决实际问题的时候会得到背离日常经验的结论。因此下一步的工作便是考虑各种外界因素对物体运动的影响，并随之更改欧勒法的方程，使之得到更为贴合实际的运动轨迹。

正文

1. 经过课上的学习，我们可以通过下面的程序，得到Figure 1.4的运动轨迹

import pylab as pl
import math
class cannon :
    def __init__(self,i=0,air_resistance=0.00004,power=10,mass = 1,time_step=0.1,\
                 total_time=10, initial_velocity=50,initial_x=0,initial_y=0,\
                 initial_velocity_x=50*math.cos(math.pi/4),\
                 initial_velocity_y=50*math.sin(math.pi/4)):
        self.x = [initial_x] 
        self.y = [initial_y]
        self.vx = [initial_velocity_x]
        self.vy = [initial_velocity_y]
        self.v = [initial_velocity]
        self.t = [0]
        self.m = mass
        self.p = power
        self.B_2 = air_resistance
        self.dt = time_step
        self.time = total_time
    def run(self):
        _time = 0
        while(_time < self.time):
            self.x.append(self.x[-1] + self.vx[-1]*self.dt)
            self.y.append(self.y[-1] + self.vy[-1]*self.dt) 
            self.v.append(math.sqrt(self.vx[-1]*self.vx[-1] + self.vy[-1]*self.vy[-1]))         
            self.vx.append(self.vx[-1] - self.dt *(self.B_2 / self.m) *\
                           self.v[-1] * self.vx[-1])
            self.vy.append(self.vy[-1] - 9.8*self.dt - self.dt *(self.B_2 / self.m) *\
                           self.v[-1] * self.vx[-1])
            self.t.append(_time)
            _time += self.dt
    def show_results(self):
        pl.plot(self.x,self.y)
        pl.ylim(0,)
        pl.xlabel('X')
        pl.ylabel('Y')
        pl.show()
a = cannon()
a.run()
a.show_results()

可以通过改变程序中的出射角，从而得到一系列轨迹，最终结果如下：

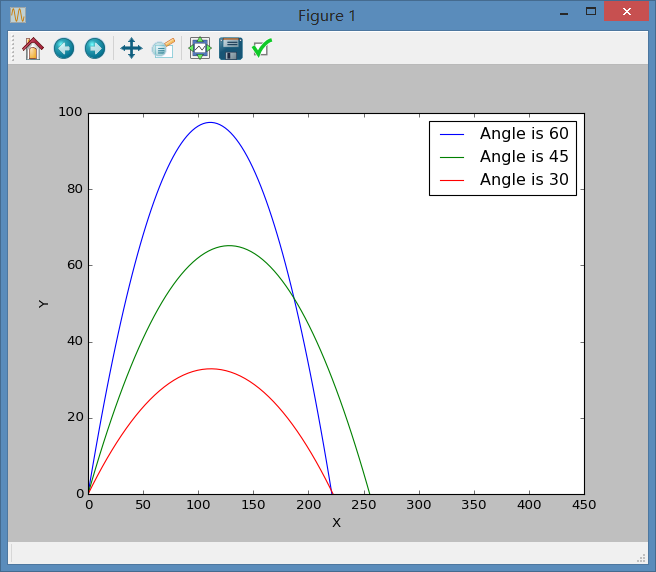
下面开始考虑实际情况
(2)首先考虑等温模型，我们有公式：

$$\begin{eqnarray*} p(y)&=&p(0)e^{-mgy/k_BT}\\ \rho&=&\rho_0exp(-y/y_0) \end{eqnarray*}$$
又因为考虑空气密度变化之后存在
$$F^*_{drag}=\frac{\rho}{\rho_0}F_{drag}(y=0)$$
故而我们将此前的公式做如下变换：
$$\begin{eqnarray*} F_{drag,x}&=&-B_2vv_x\\ F_{drag,x}&=&ma\\ a&=&-\frac{B_2vv_x}{m}\\ 修正后:a&=&-\frac{exp(-y/y_0)B_2vv_x}{m}\\ 因此：v_{x,i+1}&=&v_{x,i}-\frac{exp(-y/y_0)B_2vv_x}{m}\Delta t \end{eqnarray*}$$
以上，得到了x方向速度的修正函数，其中$y_0=k_BT/mg=1.0*10^4m$，y方向同理可写出：
$$v_{y,i+1}=v_{y,i}-g\Delta t-\frac{exp(-y/y_0)B_2vv_x}{m}\Delta t$$
于是我们可以修改程序如下,但为了便于比较，此处只给出$\theta$=45°时的轨迹

import pylab as pl
import math 
class cannon :
    def __init__(self,i=0,air_resistance=0.00004,power=10,mass = 1,time_step=0.1,\
                 total_time=10, initial_velocity=50,initial_x=0,initial_y=0,\
                 initial_velocity_x=50*math.cos(math.pi/4),\
                 initial_velocity_y=50*math.sin(math.pi/4)):
        self.x = [initial_x] 
        self.y = [initial_y]
        self.vx = [initial_velocity_x]
        self.vy = [initial_velocity_y]
        self.v = [initial_velocity]
        self.t = [0]
        self.m = mass
        self.p = power
        self.B_2 = air_resistance
        self.dt = time_step
        self.time = total_time
    def run(self):
        _time = 0
        while(_time < self.time):
            self.x.append(self.x[-1] + self.vx[-1]*self.dt)
            self.y.append(self.y[-1] + self.vy[-1]*self.dt) 
            self.v.append(math.sqrt(self.vx[-1]*self.vx[-1] + self.vy[-1]*self.vy[-1]))         
            self.vx.append(self.vx[-1] - self.dt *(self.y[-1]/10000)*(self.B_2 / self.m) *\
                           self.v[-1] * self.vx[-1])
            self.vy.append(self.vy[-1] - 9.8*self.dt - self.dt *(self.y[-1]/10000)*(self.B_2 / self.m) *\
                           self.v[-1] * self.vx[-1])
            self.t.append(_time)
            _time += self.dt
    def show_results(self):
        pl.plot(self.x,self.y,'b')
        pl.ylim(0,)
        pl.xlabel('X')
        pl.ylabel('Y')
        pl.show()
a = cannon()
a.run()
a.show_results()

此时我们可得轨迹：

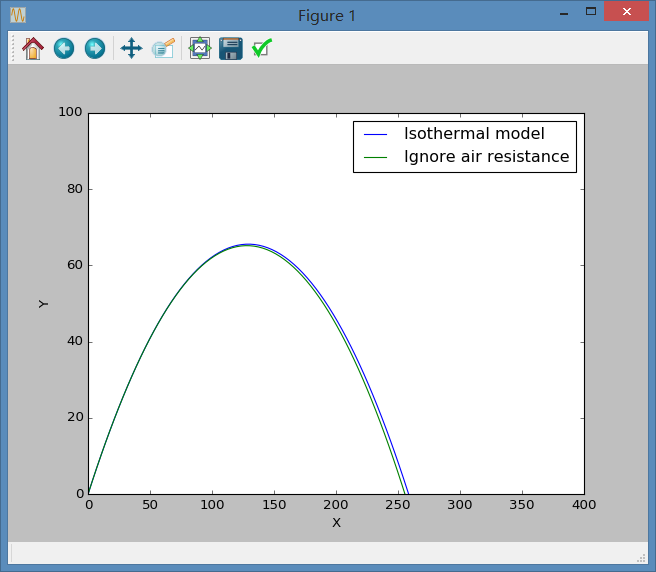
考虑等温模型后的轨迹，可见比之前要略远一点。
3.那么，当我们使用绝热模型时又会有哪些不同？
我们已知绝热模型下

$$\rho=\rho_0(1-\frac{a y}{T_0})^{\alpha}$$
其中$a=6.5*10^{-3}K/m, \alpha=2.5$,类似上一问的讨论，我们很快写出此时的方程如下：
$$\begin{eqnarray*} F^*_{drag}&=&\frac{\rho}{\rho_0}F_{drag}=(1-\frac{ay}{T_0})^{\alpha}\\ v_{x,i+1}&=&v_{x,i}-(1-\frac{ay_{i}}{T_0})^{\alpha}\frac{B_2vv_{x,i}}{m}\Delta t\\ v_{y,i+1}&=&v_{y,i}-g\Delta t-(1-\frac{ay_i}{T_0})^{\alpha}\frac{B_2vv_{x,i}}{m}\Delta t\\ \end{eqnarray*}$$
此时我们将程序进一步改写，得到：

import pylab as pl
import math 
class cannon :
    def __init__(self,i=0,air_resistance=0.00004,power=10,mass = 1,time_step=0.1,\
                 total_time=10, initial_velocity=50,initial_x=0,initial_y=0,\
                 initial_velocity_x=50*math.cos(math.pi/4),\
                 initial_velocity_y=50*math.sin(math.pi/4)):
        self.x = [initial_x] 
        self.y = [initial_y]
        self.vx = [initial_velocity_x]
        self.vy = [initial_velocity_y]
        self.v = [initial_velocity]
        self.t = [0]
        self.m = mass
        self.p = power
        self.B_2 = air_resistance
        self.dt = time_step
        self.time = total_time
    def run(self):
        _time = 0
        while(_time < self.time):
            self.x.append(self.x[-1] + self.vx[-1]*self.dt)
            self.y.append(self.y[-1] + self.vy[-1]*self.dt) 
            self.v.append(math.sqrt(self.vx[-1]*self.vx[-1] + self.vy[-1]*self.vy[-1]))         
            self.vx.append(self.vx[-1] - self.dt *pow((1-(0.0065*self.y[-1])/300),2.5)*\
                           (self.B_2 / self.m) *self.v[-1] * self.vx[-1])
            self.vy.append(self.vy[-1] - 9.8*self.dt - self.dt *\
            pow((1-(0.0065*self.y[-1])/300),2.5)*(self.B_2 / self.m) *\
                           self.v[-1] * self.vx[-1])
            self.t.append(_time)
            _time += self.dt
    def show_results(self):
        pl.plot(self.x,self.y,'g')
        pl.ylim(0,)
        pl.xlabel('X')
        pl.ylabel('Y')
        pl.show()
a = cannon()
a.run()
a.show_results()

得到如下图像，发现与不考虑空气密度情况的差别很小，几乎看不出来（关于此处差异如此之小后面会有进一步讨论）：

4.在此基础上（绝热模型），我们继续考虑地表温差造成的影响，我们有：$B^{ref}_2(\frac{T_0}{T_{ref}})^{\alpha}$来取代公式中的$B_2$,因此模型可以进一步写成如下形式：

$$\begin{eqnarray*} B^*_2&=&(1-\frac{ay}{T_0})^{\alpha}B^{ref}(\frac{T_0}{T_{ref}})^{\alpha}\\ F_{drag}&=&-B^*_2vv_x\\ v_{x,i+1}&=&v_{x,i}-(1-\frac{ay}{T_0})^{\alpha}\frac{B^{ref}}{m}(\frac{T_0}{T_{ref}})^{\alpha}\Delta t\\ v_{y,i+1}&=&v_{y,i}-g\Delta t-(1-\frac{ay}{T_0})^{\alpha}\frac{B^{ref}}{m}(\frac{T_0}{T_{ref}})^{\alpha}\Delta t\\ \end{eqnarray*}$$
我们可以进一步更改程序如下：

import pylab as pl
import math 
class cannon :
    def __init__(self,i=0,air_resistance=0.00004,power=10,mass = 1,time_step=0.1,\
                 total_time=10, initial_velocity=50,initial_x=0,initial_y=0,\
                 initial_velocity_x=50*math.cos(math.pi/4),\
                 initial_velocity_y=50*math.sin(math.pi/4)):
        self.x = [initial_x] 
        self.y = [initial_y]
        self.vx = [initial_velocity_x]
        self.vy = [initial_velocity_y]
        self.v = [initial_velocity]
        self.t = [0]
        self.m = mass
        self.p = power
        self.B_2 = air_resistance
        self.dt = time_step
        self.time = total_time
    def run(self):
        _time = 0
        while(_time < self.time):
            self.x.append(self.x[-1] + self.vx[-1]*self.dt)
            self.y.append(self.y[-1] + self.vy[-1]*self.dt) 
            self.v.append(math.sqrt(self.vx[-1]*self.vx[-1] + self.vy[-1]*self.vy[-1]))         
            self.vx.append(self.vx[-1] - self.dt *pow((1-(0.0065*self.y[-1])/300),2.5)*\
                           (self.B_2 / self.m)*pow((263/300),2.5) *self.v[-1] * self.vx[-1])
            self.vy.append(self.vy[-1] - 9.8*self.dt - self.dt *\
            pow((1-(0.0065*self.y[-1])/300),2.5)*(self.B_2 / self.m) *pow((263/300),2.5)*\
                           self.v[-1] * self.vx[-1])
            self.t.append(_time)
            _time += self.dt
    def show_results(self):
        pl.plot(self.x,self.y,'y')
        pl.ylim(0,)
        pl.xlabel('X')
        pl.ylabel('Y')
        pl.show()
a = cannon()
a.run()
a.show_results()

得到如下图像：

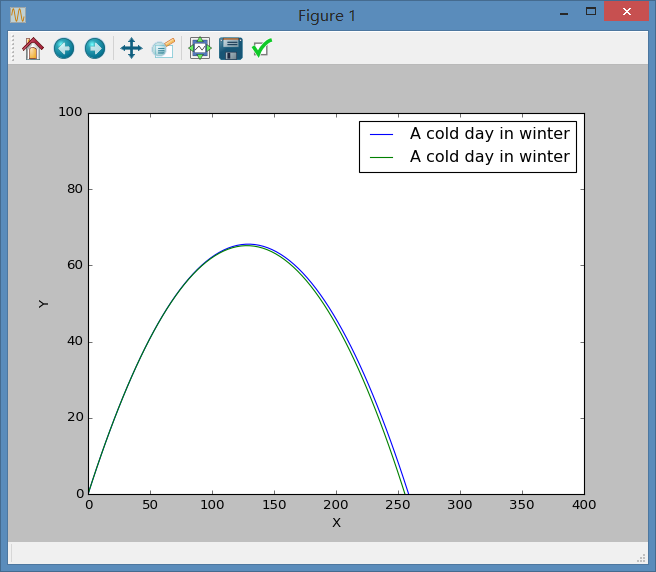
其中黄线为此时轨迹，注此时取地表温度为-10℃ 即263K，蓝线依然为不考虑空气密度情况下的轨迹
5. 我们可以在此基础上更改初射角$\theta$，得到一系列轨迹，同时又可改变地表温度$T_0$,从而获得如下两组图像：


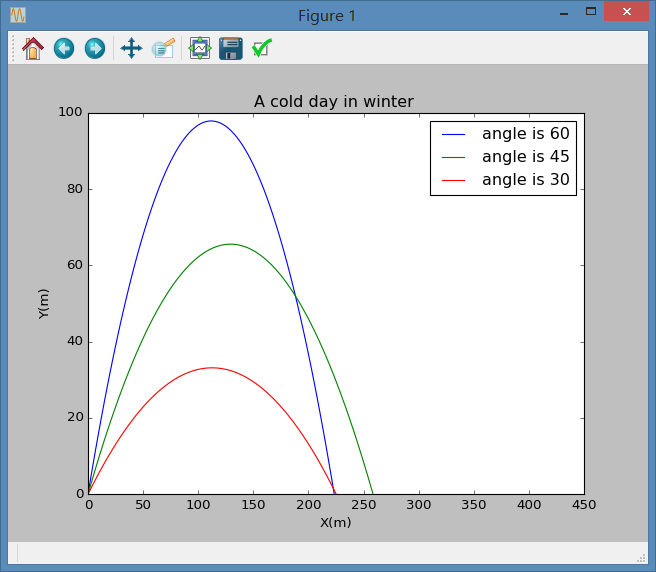
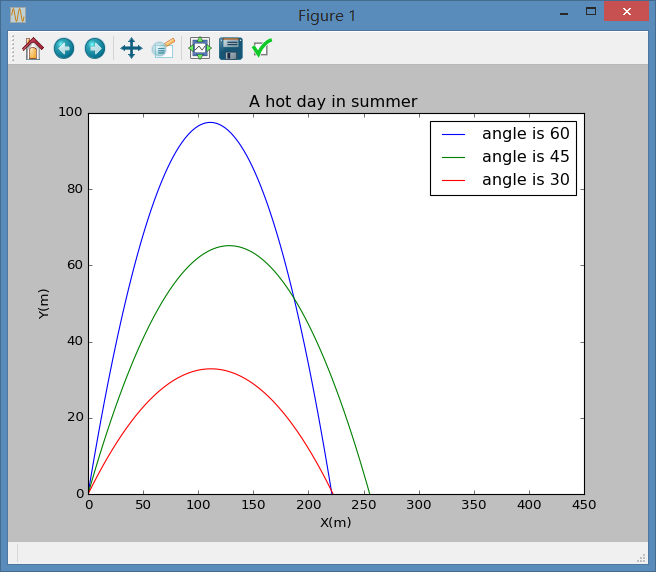
可见两组图有细微差别。

结论

我们可以通过对原有程序的修改，进一步得到更符合实际的运动轨迹，如上图。
反思：1.在写程序时遇到过如下问题，在此提出以防止日后再错，首先是用Python写程序时，尤其在打公式的时候，极容易犯错，在作业过程中多次出现如下提示
其实就是忘记在v的后面注明v[-1]，诸如此类，所以可以考虑现在纸上将其写清楚再编辑。
　　　2.轨迹图像差异过小导致无法明显看出差异，其实可以更改系数$B_2$的数值，在以上程序中，我们采用的是书中提出的数值，为$4*10^{-5}$,当我们将其改为$4*10^{-3}$,则结果会有明显不同，以最后两组图为例，我们可以得到修改后的图像如下：


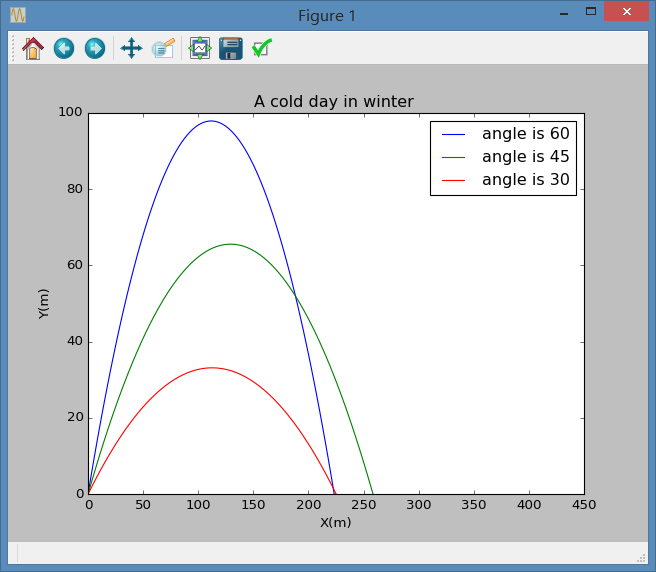
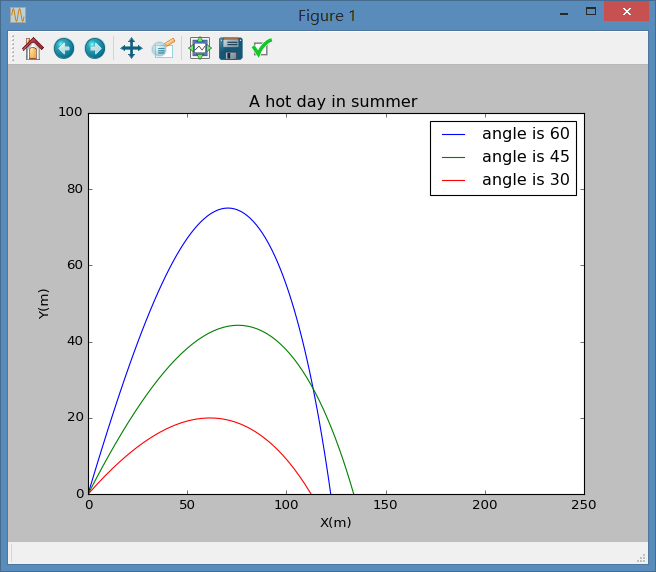
这样我们得到的差别就很明显了

致谢

老师的PPT：Chapter 2 Realistic Projectile Motion和Matplotlib Tutorial。
张梓桐同学帮忙指出之前提到的小错误。