@w460461339 2018-10-13T11:48:31.000000Z 字数 3391 阅读 971

机器学习实战Day12：PCA

MachineLearning

0.参考

这篇说的超赞
http://blog.codinglabs.org/articles/pca-tutorial.html

下面这篇一般般，甚至应该是只讲了从N维降到1维的情况，不过对于理解也有一定帮助。
http://blog.csdn.net/lu597203933/article/details/41544547

1.PCA原理说明

1.1 降维的向量和矩阵表示

1）首先来看下向量内积的两种表示方法。
首先是多项式：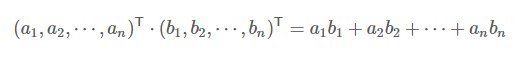
接着是高中熟悉的角度和膜方式：

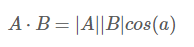
当|B|=1时，即向量B长度为1时，有：

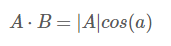
这表明，当向量B长度为1时，向量A和向量B的内积等于向量A在向量B上的投影。

当其中一个作为基的向量长度是1时，向量的乘积等于另一个向量在这个向量上的投影；
当其中一个作为基的向量长度不是1时，向量的乘积等于另个一个向量在这向量上投影的放缩。

2）基。可以理解为一组线性无关的向量。注意，基的个数决定了它能代表几维空间的向量，而不是基的长度。比如x1=[0,0,1]T和x2=[0,1,0]T这两个基，虽然基本身是3维的向量，但只能两者只能用来组成2维空间的向量。
3）向量的基描述，对于向量（3,2），我们其实描述的是它在这组基(1,0),(0,1)上的投影。那么对于任意一组基，想要确定一个向量，计算该向量在每个基上的投影即可。比如对于同样是二维空间的基,,那么(3,2)在这组基上的坐标为：
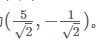
4）根据1）和3）关于向量的描述和内积的定义，我们不难发现，上述新坐标的计算可以用：基*原坐标，来得到。那么把它写成矩阵形式，有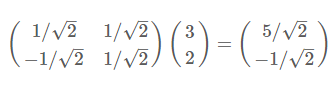：。其中左边矩阵每一行表示一个基的元素，右边矩阵每一列表示一个原坐标。那么，当右边矩阵的行数变小了，就实现了对原数据的降维变换。
5）降维的一般描述：一般的，如果我们有M个N维向量（N个特征），想将其变换为由R个N维向量表示的新空间中（可以理解为在3维空间中，把3维空间的点降维映射到一个面上），那么首先将R个基按行组成矩阵A，然后将向量按列组成矩阵B，那么两矩阵的乘积AB就是变换结果，其中AB的第m列为A中第m列变换后的结果。这里注意，当R小于n时，就实现了降维。

1.2 降维优化目标

当然，不是随便降维就可以的，我们希望，降维后，原数据的损失尽量的小，或者说，使得降维后的数据，仍能够尽可能的区分样本。

1）考虑从n维降到1维的情况。比如下图，是从2维降到1维情况，那么若选择x轴或者y轴作为基，那么会让一些数据点在降维之后重合，使得其信息丢失，无法用来区分。那如果能够找到一条直线，使得数据点之间尽量分散，区分度高，那么这个降维就算很成功。
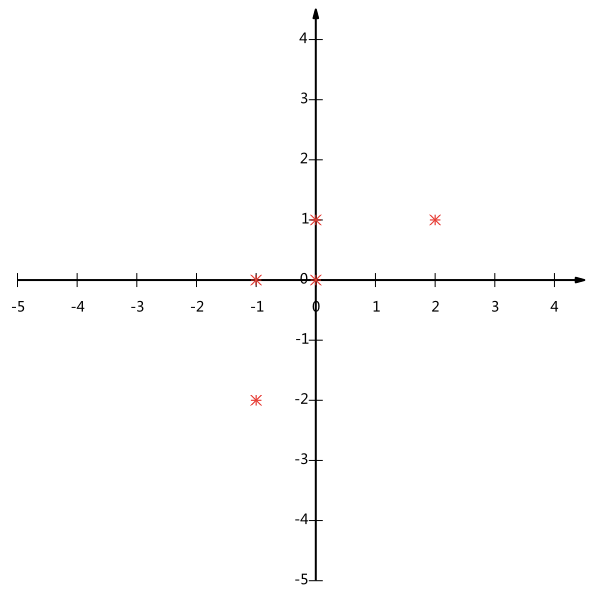
2）1）中说的区分度高，分散，我们可以用方差来表示。即，我们希望，在降维之后，数据在该维度上的方差尽可能的高。
3）考虑从3维降到2维的情况，那么2维中的其中一维我们已经找到，即方差最大的方向。那剩下一维呢？观察下图，对于图a，两坐标轴之间夹角不等于90°，那么当A沿着坐标轴x1增大时，A的x2坐标也会增大。这表示x1和x2之间有一定关联性，表示的信息有重复。而对于图b，则不会出现这样的情况。
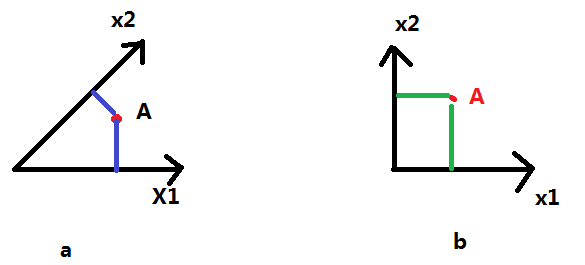
4）因此，为了尽可能多的表示信息，并且彼此之间不重复，在3维降到2维时，在保持方差大（指在每一维度上）的情况下，令第二维与第一维正交，才可以保留最多的信息。
5）因此，我们得出了两条可以作为计算依据的约束：
1.令样本在降维后每一维上的映射的方差尽可能大。
2.令降维后每一维之间正交。（对应于维数两两之间协方差为0）

1.3 协方差矩阵与优化

1）我们希望将两个约束放在一个矩阵里，从而方便计算。我们有协方差矩阵。
假设我们只有a和b两个字段，那么我们将它们按行组成矩阵X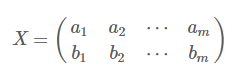：，其中每一列表示一个样本，每一行表示一个特征，且每个特征做过去均值处理；
然后我们用X乘以X的转置，并乘上系数1/m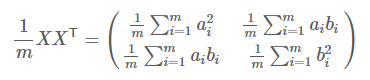：我们发现，对角线上是方差，其他地方是协方差。
2）根据1）我们得到，设我们有m个n维数据记录，将其按列排成n乘m的矩阵X，设 $C=\frac{1}{m}XX^T$ ，则C是一个对称矩阵，其对角线分别个各个字段的方差，而第i行j列和j行i列元素相同，表示i和j两个字段的协方差。
3）那么，根据协方差矩阵，我们发现我们的优化条件变成了，等价于将协方差矩阵对角化：即除对角线外的其它元素化为0，并且在对角线上将元素按大小从大到小排列，这样我们就达到了优化目的。
4）我们来比较一下，原始的样本矩阵，和降维后的样本矩阵，他们的协方差矩阵之间的关系。设原始数据矩阵X对应的协方差矩阵为C，而P是一组基按行组成的矩阵，设Y=PX，则Y为X对P做基变换后的数据。设Y的协方差矩阵为D，我们推导一下D与C的关系：
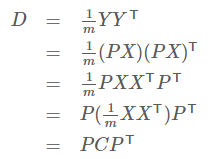
5）现在事情很明白了！我们要找的P不是别的，而是能让原始协方差矩阵对角化的P。换句话说，优化目标变成了寻找一个矩阵P，满足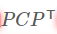是一个对角矩阵，并且对角元素按从大到小依次排列，那么P的前K行就是要寻找的基，用P的前K行组成的矩阵乘以X就使得X从N维降到了K维并满足上述优化条件。

1.4 计算

由上文知道，协方差矩阵C是一个是对称矩阵，在线性代数上，实对称矩阵有一系列非常好的性质：

1）实对称矩阵不同特征值对应的特征向量必然正交。

2）设特征向量λ重数为r，则必然存在r个线性无关的特征向量对应于λ，因此可以将这r个特征向量单位正交化。

由上面两条可知，一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量，设这n个特征向量为e1,e2,⋯,en,我们将其按列组成矩阵：
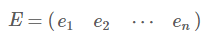
image_1c05s65ms1jr718ilvg28vj1ol8p.png-2.1kB
则对协方差矩阵C有如下结论：
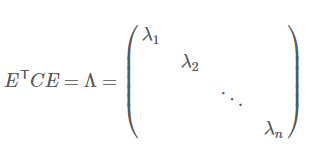
image_1c05s765sbqjip913l21s5m17uu96.png-6.6kB

那么这里特征值就是降维后的方差，我们从大到小选择k个特征值λ，这k个特征值对应的特征向量，就是我们要的基。

到这里，我们发现我们已经找到了需要的矩阵P：

                        P=ET（E矩阵的转置）

P是协方差矩阵的特征向量单位化后按行排列出的矩阵，其中每一行都是C的一个特征向量。如果设P按照ΛΛ中特征值的从大到小，将特征向量从上到下排列，则用P的前K行组成的矩阵乘以原始数据矩阵X，就得到了我们需要的降维后的数据矩阵Y。

2.代码

这里我的代码只是从2维映射到了1维。

from numpy import *
def loadDataSet(fileName,delim='\t'):
    fr=open(fileName)
    stringArr=[line.strip().split(delim) for line in fr.readlines()]
    datArr=[list(map(float,line)) for line in stringArr]
    return mat(datArr)
def pca(dataMat,topNfeat=9999999):
    # 求每列平均值
    meanVals=mean(dataMat,axis=0)
    # 每一列去除平均值
    meanRemoved=dataMat-meanVals
    # 计算协方差矩阵
    covMat=cov(meanRemoved,rowvar=0)
    # 计算协方差矩阵的特征值和特征向量
    eigVals,eigVects=linalg.eig(mat(covMat))
    # 特征值排序，从小到大
    eigValInd=argsort(eigVals)
    #
    eigValInd=eigValInd[:-(topNfeat+1):-1]
    redEigVects=eigVects[:,eigValInd]
    lowDDataMat=meanRemoved*redEigVects
    reconMat=(lowDDataMat*redEigVects.T)+meanVals
    return lowDDataMat,reconMat
def plotResult(dataMat,reconMat):
    import matplotlib.pyplot as plt
    fig=plt.figure()
    ax=fig.add_subplot(111)
    ax.scatter(dataMat[:,0].flatten().A[0],dataMat[:,1].flatten().A[0],marker='^',s=90)
    ax.scatter(reconMat[:,0].flatten().A[0],reconMat[:,1].flatten().A[0],marker='o',s=90,c='red')
    plt.show()