@w460461339
2018-11-01T02:03:51.000000Z
字数 1945
阅读 1685
LightGBM
MachineLearning
0、参考
http://mlexplained.com/2018/01/05/lightgbm-and-xgboost-explained/
https://www.hrwhisper.me/machine-learning-lightgbm/
1、基本介绍
Light-GBM也是GBDT框架里面的东西,在我看来,它主要做了以下几点改变。
1)树的生成策略上的改变。
2)树在生成时,分叉策略上的改变。
2、Level-wise vs Leaf-wise
对于数据集S,包含m个样本以及n个特征。
如果采用相同的分支策略(比如都是信息增益或者基尼系数),那么最终都会生成完全相同的完全决策树。
但是,完全决策树生成过程不同。
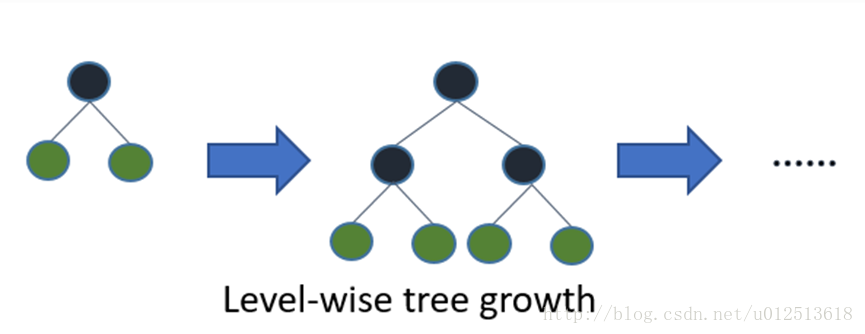
- 1)Level-wise生成过程。(又称depth-first,和BFS对应)。
- 2)leaf-wise生成过程。
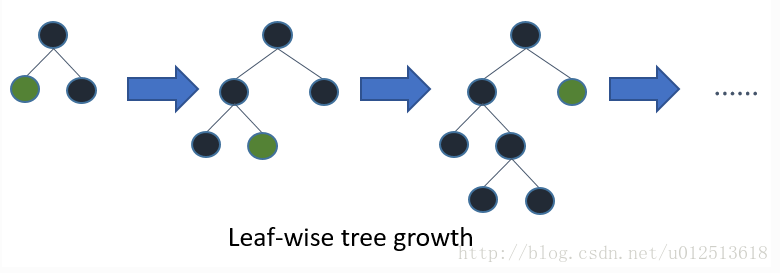
从上面两幅图可以看到,两种生成策略,过程上的决策树是不一样的。
而又因为我们会使用预剪枝或者早停策略,所以得到的决策子树显然也会是不一样的。
那么两种方法得到的不同树,表现好坏如何呢?
level-wise倾向于齐头并进,而leaf-wise倾向于先把某一块做到比较好。
那么从loss的角度看,leaf-wise会使得全局loss降低更低。(这个其实有点贪婪算法的意思)
所以,单棵树上面,leaf-wise相比于level-wise,会更快达到一个较低的loss水平。
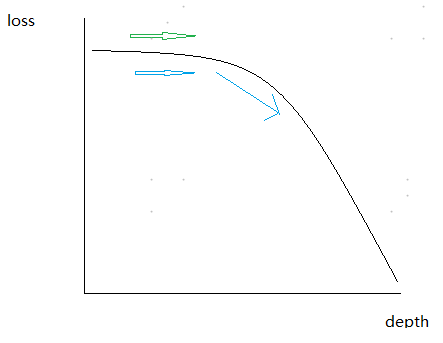
为什么这么说?因为深度和loss的关系看,在最开始的时候loss并不会随着depth的增加而下降的快;但是一旦到了后期,depth增加一点点,loss就会下降很多。
而leaf-wise是率先到达了loss下降快速的区域,而level-wise花了同等时间,却还在loss缓慢下降的地方溜达。虽然level-wise可以在loss下降缓慢的地方同时优化多个浅层分支,但是仍然没有一个深层分支的loss下降的多。
3、直方图算法
3.1 基本概念
决定了树的生成思路,那么具体树的每个节点该如何分支是接下来要考虑的主要问题。
传统的分支方法,是基于这个节点上,所有的特征以及所有特征的取值,进行分支实验,然后根据信息增益或者基尼系数,或者其他什么标准,来选择最好的特征已经分支点。
那么这样的情况下, 计算量是O(),超大!
现在考虑,我们对每个特征做一个直方图,或者分桶。
比如原来2个特征(假设都是连续特征),4个样本,那么一共要尝试8次。
| 样本序号 | 特征1 | 特征2 |
|---|---|---|
| 1 | 1 | 10 |
| 2 | 3 | 15 |
| 3 | 2 | 20 |
| 4 | 4 | 25 |
现在,对每个特征,都分两个桶,把样本归到不同的桶里面。(比如对于第一个特征,把小于等于2的归于一个桶,大于2的归到另一个;第二个特征则是20为分界线。分别用0和1表示)
那么,分完桶后可以用下面的表格来表示。
| 样本序号 | 特征1 | 特征2 |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 1 | 0 |
| 3 | 0 | 1 |
| 4 | 1 | 1 |
这样虽然还是2个特征4个样本,但是特征的取值每个特征的取值只有两种了,所以一共只需要计算O()这么多次即可。
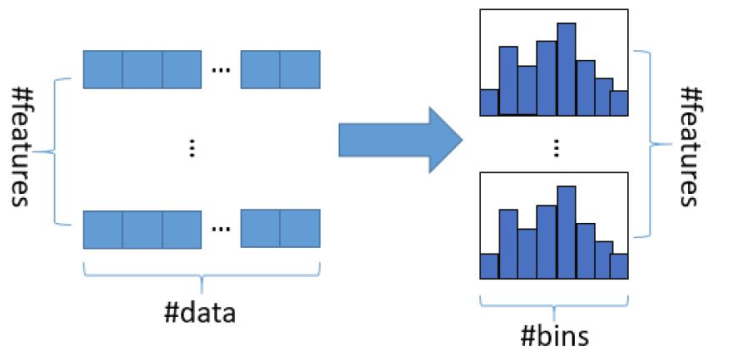
当然,桶的数量和精度正相关,和计算效率逆向关。如何分桶也是需要仔细考量的,这里不多说。
3.2 直方图计算小技巧
我们计算出了父节点——黑色节点——每个特征的直方图,并根据直方图进行分支,得到了橙色和灰色两个子节点。
那么,为了计算橙色节点和灰色节点该怎么分支,我们需要进一步对计算被分到橙色节点的样本上所有特征的直方图,灰色节点同理。
tricky的地方就在这里。
当我们计算完橙色节点上的直方图后,我们不需要计算灰色节点的直方图了,直接通过黑色节点减去橙色节点,即可完成灰色节点的计算。

可以看一下。
原始数据,分桶标准是:
1、第一个特征,把小于等于2的归于一个桶,大于2的归到另一个;
2、第二个特征则是20为分界线。
3、分别用0和1表示
| 样本序号 | 特征1 | 特征2 | 分桶后 | 特征1 | 特征2 |
|---|---|---|---|---|---|
| 1 | 1 | 10 | 分桶后 | 0 | 0 |
| 2 | 3 | 15 | 分桶后 | 1 | 0 |
| 3 | 2 | 20 | 分桶后 | 0 | 1 |
| 4 | 4 | 25 | 分桶后 | 1 | 1 |
假设根据特征1来分,即特征1取值为0的为橙色,取值为1的取灰色。得到橙色节点的样本以及分桶结构。
| 样本序号 | 特征1 | 特征2 | 分桶后 | 特征1 | 特征2 |
|---|---|---|---|---|---|
| 1 | 1 | 10 | 分桶后 | 0 | 0 |
| 3 | 2 | 20 | 分桶后 | 0 | 1 |
显然,灰色节点的分桶结果无序计算,就可以直接得到。
问:
是不是每个节点计算分桶-histogram的标准必须要一致,才可以这么计算。
