@w460461339
2018-11-30T07:04:47.000000Z
字数 2648
阅读 2029
卷积和滤波
MachineLearning
0、傅里叶变换参考
基本傅里叶变换理解:
https://zhuanlan.zhihu.com/p/19763358
离散傅里叶变换:
https://blog.csdn.net/lovehua365/article/details/79110950
图像傅里叶变换:
https://blog.csdn.net/ViatorSun/article/details/82387854
卷积解释:
https://blog.csdn.net/qq_27531383/article/details/72534608
卷积和傅里叶变换:
https://blog.csdn.net/hnyzyty/article/details/52814192
图像傅里叶变换的特性:
https://blog.csdn.net/ViatorSun/article/details/82387854
1、参考
傅里叶变化,时域和频域的zhua:
https://blog.csdn.net/struggle_for_m/article/details/51207370
https://blog.csdn.net/sphone89/article/details/7370103?utm_source=blogxgwz1
一维的时域和频域转换很好理解,下面这张图就能理解了。红色表示时域,蓝色直线表示频域。
蓝色直线横轴是频率变换,竖直是幅度。(同一频率叠加的越多,幅度也会越高把)
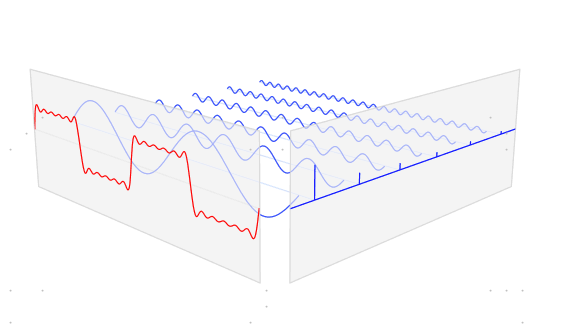
下面是二维图像的傅里叶变化参考。
左边是原图,右边是幅度图。中心为x方向频率为0,y方向频率为0的振幅。
所以可以理解为,左边那幅图,换成频率域后,频率主要集中在低频,然后高频主要是沿两轴扩展,单独分布,比如四角区域,都是相对高频的地方,都是没有分布的。
另外注意,频率图和原图位置没有任何对应关系!
频率图反应的是原图在灰度图上变化的梯度。

然后卷积为什么又被称为过滤器呢?
https://blog.csdn.net/hnyzyty/article/details/52814192
卷积操作之后,相当于把某些频率过滤掉了。
时域上的卷积,等价于频域上的相乘。
2、总结
2.1 什么是傅里叶变化以及图像如何做傅里叶变换
1)傅里叶变换把是时域或者空间域上的函数,变成频率域上函数的累加。
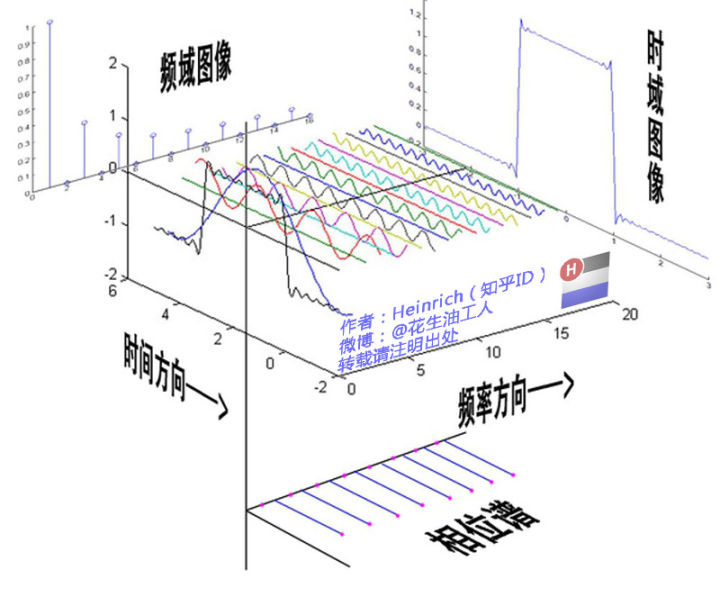
2)离散/连续,周期/非周期都可通过周期变换的频率维度上的信息。
例子见上面离散傅里叶参考链接。3)图像可以看做是二维离散函数f((x,y))=gray,输出是每个像素点的灰度值。
4)因此图像也可以做傅里叶变换,并且中心化之后,可以得到:

注意,频谱图任意位置和原图中任意位置没有任何对应关系。假设中心点坐标是(0,0),在频谱图中(2,2)表示的是x方向上频率是2,y方向上频率也是2的正弦波叠加的亮度是多少(差不多一个意思)。重申:和原图没有关系!
2.2 卷积和傅里叶变化

还是这张图,对于正弦波 而言,我们需要知道他的:
振幅:A
频率:w
相位:θ
才能够确定它。
另外,A=0时正弦波就变现为一条直线。
1)卷积可以分为离散函数和连续函数的卷积。可以参考开头给出的连接:
离散卷积:
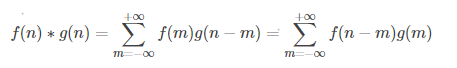
2)那么观察,对和进行卷积,会得到:
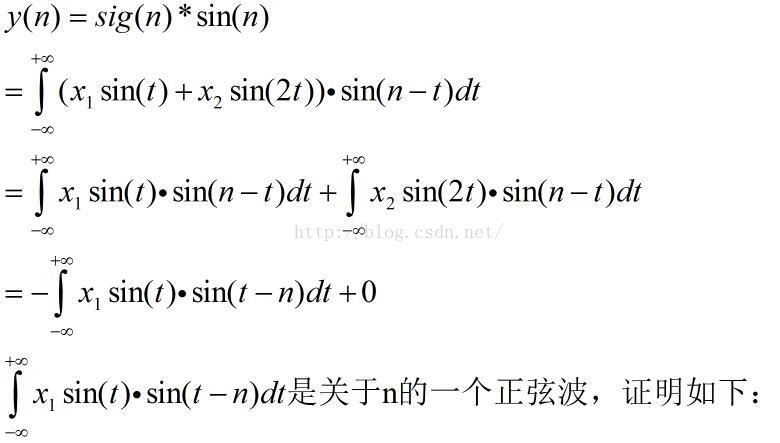
3)我们通过对f(t)做关于g(t)的卷积,得到了f(t)中的振幅x1.相当于,我们利用g(t)提取到了f(t)中的某一种频率的正弦波。
4)反映到频谱上,相当于对频率做了一个滤波,过滤掉了频率为那个正弦波,只留下频率为的正弦波。
5)对应到图像上。如果把图像看做是无限个正弦波的集合,而卷积核也同理,是一个无限个正弦波的集合。
6)那么,两者的卷积再时域上会有两种表现:
1、简单离散函数的卷积,逐项相乘求和就行了,这个是正常的表现。
2、如果把每块区域看成是正弦函数的集合,卷积就变成了这些正弦函数之间求积分,只会剩下部分感兴趣频率的振幅以及积分值。7)那么,从这个角度来说,对图像做卷积,相当于用卷积核在图像上做特征提取。我们通过人为的设定一些卷积核,可以方便的从图像中提取出一些特征。比如横向和纵向的sobel算子来提取边间,canny来提取边界等等。
8)那么,在我们看来,CNN网络成功的原因,是因为它不需要人工提取特征,而通过网络自动学习卷积核的参数,从而提取到最能够满足任务的特征。
2.3 傅里叶的特征和CNN的问题
- 1)图像的傅里叶变换有很多特性,这里就说一下平移不变形。
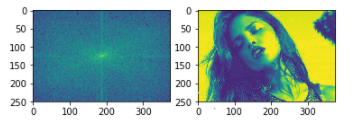 图1
图1
 图2
图2
2)观察以上两幅图像,右边是原始图片,左边是对应的频谱图。可以看到,两张原图的区别在于第二张图片在第一张图片中间切断后上下交换了。但是两幅图像的频率图是一模一样的。
下面是两个频谱图相减的结果,可以看到,全都是0,表示真的一模一样了!

3)然后,我们交换图中的某些特征:
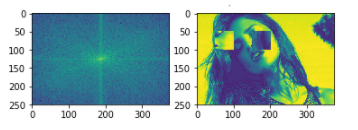 图3
图3
继续来看频谱图之间的差别:
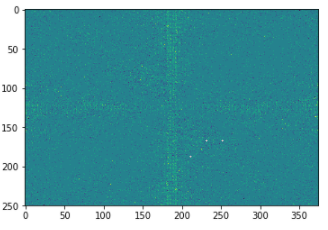
4)可以看到,频谱之间有差别,但是这些差别非常的不明显(因为没有明显的亮色区域)。
5)因此,我们发现了,对于原始图像上的两个特征(比如嘴巴和鼻子),若是他们的相对位置变换,在频谱上的变换非常小,会使得滤波器难以发现这些变换(但却仍然能够发现这些特征)。对应到CNN网络中,表现的就是,对于人脸,如果交换鼻子和嘴巴的位置,卷积核难以发现这些变化,能发现的只有鼻子和嘴巴的存在,因此还是认为是一张人脸(但其实不符合人脸的逻辑)。
以上,是我对CNN网络对特征之间相对位置不敏感的一种解释。
3、问题
 图1
图1
这幅图可以解释为什么下面两幅图的傅里叶变换为什么是一样的。
 图2
图2
 图3
图3
对于图2而言,我们相当于取图1中红色框以及其对应的傅里叶变化后得到的频谱图。
而对于图3,我们相当于取图1中绿色狂以及其对应的傅里叶变化后得到的频谱图。
对于两幅频谱图,将其做中心化之后,我们会发现,他们是一模一样的。
这是因为,对于DFT,即快速傅里叶变换而言,它将输入的内容认为是一个周期,并以此对一个连续的周期函数进行傅里叶变换,从而得到了目标值。
但是,当我们对图4做傅里叶变换时,它得到的频谱图并不是图5的频谱图的周期性重复,而是完全另外一种图:
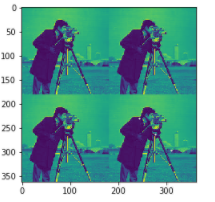 图4
图4
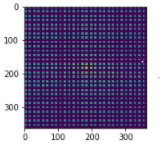 图4-频谱图
图4-频谱图
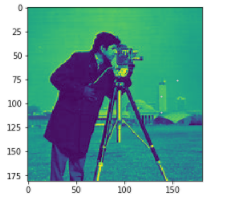 图5
图5
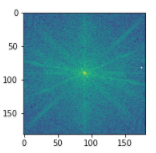 图5-频谱图
图5-频谱图
这其实可以简单的理解为,图4中的4幅小图,已经被认为是一个整体,而不是简单的周期性重复。故而在计算灰度梯度时,和图5的图不同。
