西瓜书——3.3 LDA（线性判别分析）

MachineLearning

0、参考：

LDA：
西瓜书3.3
http://www.cnblogs.com/pinard/p/6244265.html#!comments
https://blog.csdn.net/liuweiyuxiang/article/details/78874106
http://www.cnblogs.com/engineerLF/p/5393119.html

拉格朗日乘子法：
https://blog.csdn.net/lijil168/article/details/69395023

协方差矩阵：
http://pinkyjie.com/2010/08/31/covariance/

正定矩阵：
https://baike.baidu.com/item/%E6%AD%A3%E5%AE%9A%E7%9F%A9%E9%98%B5

1、瑞利商与广义瑞利商

• 1）首先看一下式子。

  $$R(X)=\frac{X^HAX}{X^HX}$$ 这里的$X^H$表示为转置。我们会有以下不等式
  $$λ_{min}≤\frac{X^HAX}{X^HX}≤λ_{max}$$
  其中$λ_{min}$和$λ_{max}$表示矩阵A的最小特征值和最大特征值。
  以上就是瑞利商。

• 2）下面来看看更一般的广义瑞利商。广义瑞利商有如下形式

  $$R(X)=\frac{x^HAx}{x^HBx}$$ ，其中A和B都是Hermitan矩阵，即它的转置和自己相同。我们将如下式子$x=x^{'}*B^{-\frac{1}{2}}$带入上式，得到
  $$R(X)=\frac{(x^{'}*B^{-\frac{1}{2}})^HA(x^{'}*B^{-\frac{1}{2}})}{(x^{'}*B^{-\frac{1}{2}})^HB(x^{'}*B^{-\frac{1}{2}})}$$

化简，得到：

即又得到了我们的瑞利商的形式，同样，我们取$λ_{min}$和$λ_{max}$表示矩阵$B^{-1}A$的最大最小特征值，来表示我们的R（x）的取值范围。

2、二分类LDA问题

2.1 符号含义

x : 表示训练样本，使用列向量表示，假设有n维
$x_{ji}$：表示第i类中的第j个样本
$C$：表示有C类样本
$μ_i$：表示第i类训练样本的均值,也是列向量 （i=1,2,…,C）
$M_i$：表示第i类训练样本的数目
M：表示训练样本的总数目 $M=\sum_{i=0}^{C}M_i$
μ：是所有样本的均值向量，也是列向量 $μ=\frac{1}{M}\sum_{i=1}^{M}x_i=\frac{1}{C}\sum_{i=1}^{C}μi$
$D_i$：表示第i类样本集合
$S_w$：表示类内散度矩阵，w是within的简写
$S_b$：表示类间散度矩阵，b是between的简写
$w$：这里指超平面参数，即$y=w^Tx$，$w$也是一个列向量或由列向量构成的矩阵。

2.2 推导过程

• 1）首先通过图来看一下我们的目标。如下图,对于图中所示的蓝和红两类点，我们希望找到通过更低维度的信息将其分开。具体来说，我们希望找到一条直线，将这些点投影到直线上，使得投影后的点，每个类内尽可能的靠拢，类和类之间尽可能离散。从图中我们可以看到，右边的直线的分割，显然好于左边的直线分割。

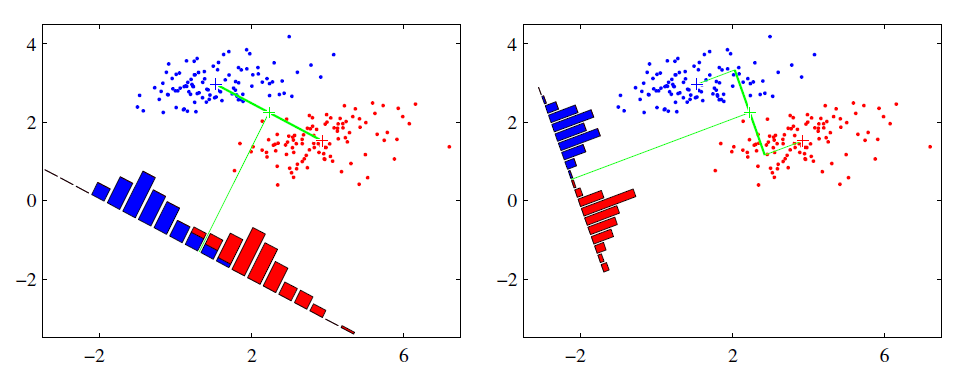
• 2）对于我们的问题，二分类问题，C=2，即我们只有两类样本（0和1）。我们假设我们的目标直线是$y=w^Tx$,注意这里的w和x都是列向量，w经过转置之后和x相乘，得到直线上的一个样本点。

类间距离

• 3）我们用两个类的均值点来代表两个类。那么对于第0类样本，它们的均值点$μ_0$在直线上的投影为$w^Tu_0$;第1类样本同理。

• 4）那么两个类在直线上的距离为$||w^Tμ_0-w^Tμ_1||^2$,我们希望这个值尽可能的大。

类内距离

• 5）类内距离，我们希望用协方差矩阵来表示。对于第0类中的某一个样本$x_i$,它的每个维度和第0类均值点$μ_0$之间的离散程度，可以用$(x_i-μ_0)(x_i-μ_0)^T$表示，得到是一个n*n的矩阵，类似于，对角线元素表示的是每个维度上的方差，其他元素表示的偏差的相关性。：
  

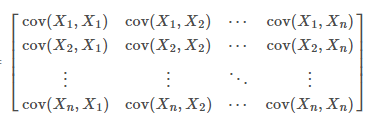
• 6）那么把描述每个点$x_i$和其类中心点$u_i$的离散程度的协方差矩阵加起来，就得到了描述一个类离散程度的矩阵，我们用$\sum_{0}$和$\sum_{1}$表示，我们希望这两个值尽可能的小，即希望$\sum_{0}+\sum_{1}$最小。

• 7）那么对于直线上的点，同理，只不过把$x_i$用$w^Tx_i$代替，$μ_i$用$w^Tμ_i$代替。最终得到，在直线上，每个类的协方差矩阵为$w^T\sum_{0}w$和$w^T\sum_{1}w$。同理，我们希望$w^T\sum_{0}w+w^T\sum_{1}w$尽可能的小。

调优式

• 8）现在我们有两个目标，一个是$||w^Tμ_0-w^Tμ_1||^2$这个尽可能的大，一个是让$w^T\sum_{0}w+w^T\sum_{1}w$尽可能的小。综合两者，我们得到目标调优式：
  

  $$argmax J(w)=\frac{||w^Tμ_0-w^Tμ_1||^2}{w^T\sum_{0}w+w^T\sum_{1}w}=\frac{w^T(μ_0-μ_1)(μ_0-μ_1)^Tw}{w^T(\sum_{0}+\sum_{1})w}$$

• 9）现在还有一点看不出来，我们令

  $$S_b=(μ_0-μ_1)(μ_0-μ_1)^T$$ , $$S_w=(\sum_{0}+\sum_{1})$$ ,那么，8）中的式子可以变为：
  $$argmax J(w)=\frac{w^TS_bw}{w^TS_ww}$$ 。

• 10）这个不就是瑞丽商的形式嘛，现在我们希望找到一个$w$，让这个式子取到最大值。首先观察，上下两个式子都还有$w$的二次项，那么也就是说，这个$J(w)$的式子的取值仅和$w$的方向有关，和$w$的取值无关。

• 11）我们假设某种取值可以令$w^TS_ww=1$,那么此时，我们的目标是$argmax(w) [w^TS_bw]$,我们取负号，得到以下内容：
  

  $$argmin(w):-w^TS_bw$$
  $$s.t. w^TS_ww=1$$

• 12）利用拉格朗日乘子法，我们可以得到下面的式子：

  $$F(w,λ)=-w^TS_bw+λ(w^TS_ww-1)$$

• 13）分别对$F(w,λ)$对$w$和$λ$求导，分别令其等于0，【不需要对λ求导，这里就不写了】有：

  $$\frac{\mathrm{d}F(w,λ)}{\mathrm{d}w}=-2S_bw+2λW_ww=0$$ 最终，有 $$λw=S_w^{-1}S_bw$$

• 14)我们发现$S_bw=(μ_0-μ_1)(μ_0-μ_1)^T*w$，别忘了$w,μ_i$都是是列向量，最终这个式子的方向是由$(μ_0-μ_1)$决定的，因此我们可以用$S_bw=(μ_0-μ_1)λ_k$来表示。

• 15）那么，对于13）中的式子，我们有$w=S_w^{-1}(μ_0-μ_1)\frac{λ_k}{λ}$。之前也说了，w的取值和大小无关，因此最后的系数不要，最终得到我们w的表达式:

  $$w=S_w^{-1}(μ_0-μ_1)$$

3、多类别LDA

当只有两个类别的时候，我们可以将其投影在一条线上，当我们有K个类别的时候呢？

虽然不是不可以投影在一条直线上，但是有没有更好的选择，比如投影在其他平面上？

3.1 符号定义

x : 表示训练样本，使用列向量表示，假设有n维
$x_{ji}$：表示第i类中的第j个样本
$C_i$：表示第$C_i$类样本,假设$C={C_1,C_2...C_k}$
$μ_i$：表示第i类训练样本的均值,也是列向量 （i=1,2,…,C）
$N_i$：表示第i类训练样本的数目
M：表示训练样本的总数目 $M=\sum_{i=0}^{C}N_i$
μ：是所有样本的均值向量，也是列向量 $μ=\frac{1}{M}\sum_{i=1}^{M}x_i=\frac{1}{C}\sum_{i=1}^{C}μi$
$D_i$：表示第i类样本集合
$S_w$：表示类内散度矩阵，w是within的简写
$S_b$：表示类间散度矩阵，b是between的简写
$w$：这里指超平面参数，即$y=w^Tx$，$w$也是一个列向量或由列向量构成的矩阵。【这里的w大概率是一个矩阵了，因为除了线以外，其他超平面都需要一组基来描述,假设基是d维的】

3.2 推导

• 1）首先，我们定义一下全局离散度

  $$S_t=\sum_{i=1}^{M}(x_i-μ)(x_i-μ)^T$$

• 2）然后，全局的协方差矩阵和：

  $$S_{wi}=\sum_{x∈X_i}(x_i-μ_i)(x_i-μ_i)^T$$
  $$S_w=\sum_{i=1}^{K}S_{wi}$$

• 3）我们认为全局的离散度由全局的协方差矩阵和以及全局的类间距离构成，因此

  $$S_b=S_t-S_w=\sum_{i=1}^{k}(μ_i-μ)(μ_i-μ)^T$$

• 4)仿照二分类，我们得到目标调优式：

  $$argmax：J(W)=\frac{W^TS_bW}{W^TS_wW}$$ .注意，这里大写的W表示，这是W是一个矩阵，因此，我们没办法用二分类问题中的方案来解这个问题。

• 5）因此，我们转换目标函数为：

  $$argmax：J(W)=\frac{\prod_{diag}w_i^TS_bw_i}{\prod_{diag}w_i^TS_ww_i}$$
  其中$\prod_{diag}A$表示对矩阵A主对角线元素的乘积。

• 6）那么上式我们可以转化为

  $$argmax：J(W)=\frac{\prod_{diag}w_i^TS_bw_i}{\prod_{diag}w_i^TS_ww_i}=\prod_{i=1}^{d}\frac{w_i^TS_bw_i}{w_i^TS_ww_i}$$

• 7）那么，6）中式子的最大值，根据瑞丽商，我们知道它等于$S_w^{-1}Sb$的前d个最大特征值的乘积。而我们的W,也可以用着d个最大特征值对应的特征向量组成。因为特征值大，表示在对应的特征向量方向上，数据离散的开，那么数据间就越容易区分。

• 8）注意这里有一个W的基的参数d，它会和$S_w^{-1}Sb$的特征值数量有关。我们发现，$Sb=\sum_{i=1}^{k}(μ_i-μ)(μ_i-μ)^T$,其依赖于不同的$u_i$,但虽然我们有k个类别，对应k个$u_i$。但是因为所有的训练样本我们都是知道，所有当知道了前k-1个$μ_i$后，最后一个$μ_k$可以由已知的所有样本的向量和减去前k-1个$μ_j$乘以其类别个数，最后除以第k类的个数得到。因此$S_b$的秩为k-1，所以W的中最多有k-1个基。