[透彻理解]由最小二乘到SVD分解 By SPP

Optimization

---

借鉴的材料

• https://www.cnblogs.com/hxjbc/p/7443630.html
• https://blog.csdn.net/macer3/article/details/48394239/
• https://zhuanlan.zhihu.com/p/57803955

前言：最近在整理项目资料，其中有一个三维点云地面部分的提取。关于其理论，在此做一个整理。

1 问题引入：二维直线的拟合问题

假设我们有：$A:(1,2),B:(0,2),C:(2,3)$三个点，现在需要对这个三个点拟合一条直线。

设这条直线的方程为$y=ax+b$ 。我们希望这条直线可以同时通过这三个点，也就是这条直线的参数要满足:

$$\left\{ \begin{array}{l} 1 \times k + b = 2\\ 0 \times k + b = 2\\ 2 \times k + b = 3 \end{array} \right.$$
这是一个超定方程。为了后面表示方便，在这里我们用$x_1,x_2$来代替$k,b$。
$$\left\{ \begin{array}{l} 1 \times {x_1} + {x_2} = 2\\ 0 \times {x_1} + {x_2} = 2\\ 2 \times {x_1} + {x_2} = 3 \end{array} \right.$$
写成矩阵的形式：
$$\begin{array}{l} \left[ \begin{array}{l} 1\,\,\,\,1\\ 0\,\,\,1\\ 2\,\,\,1 \end{array} \right]\left[ \begin{array}{l} {x_1}\\ {x_2} \end{array} \right] = \left[ \begin{array}{l} 2\\ 2\\ 3 \end{array} \right]\\ \,\,\,\,\,\,\,\,\, \uparrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \uparrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \uparrow \\ \,\,\,\,\,\,\,A\,\,\, \times \,\,\,\,\,\,x\,\,\,\,\,\, = \,\,\,\,\,\,\,b\,\, \end{array}$$
这即是我们要优化的非齐次线性方程组$Ax=b$。

这里如何假如出口基。入口基的概念？

为了方便我们接下来的理解，现在将其拆分成下面这种形式：

$$\begin{array}{l} \left[ \begin{array}{l} 1\\0\\2 \end{array} \right] \times {x_1} + \left[ \begin{array}{l} 1\\1\\1 \end{array} \right] \times {x_2} = \left[ \begin{array}{l} 2\\2\\3 \end{array} \right]{\mkern 1mu} \\ {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \uparrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \,\,\,\,\,\,\,\,\,\,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\uparrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \,\,\,\,\,\,\,\,\,\,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \,\,\,\,\,\,\,\,\,\,\,\,\uparrow \\ {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {a_1}{\mkern 1mu} {\mkern 1mu} \,\, \,\,\,\,\times \,\,\,\,{x_1}{\mkern 1mu} \, + {\mkern 1mu} {\mkern 1mu} \,\,{a_2}{\mkern 1mu} \times {x_2}{\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \,\,\,\,b \end{array}$$
这里的理解方式是，两个3维向量，经过$x_1$和$x_2$的线性组合之后，得到$b$向量。

这里更高级一点的说法是，在以$a_1,a_2$为基向量(3维)所张成的2维子空间上，寻找最接近$b$向量的向量。

把$a_1,a_2$视作基向量，画图理解。


由这个图可知，公式(4)肯定是不成立的，因为向量$b$(红色)就不在基向量$a_1,a_2$所张成的二维平面（二维子空间）里。

所以，我们在这里退而求其次，在该二维子空间中找一个向量$b'$（由基向量组成$b'=x_1*a_1+x_2*a_2$），来代替向量$b$，但是这个向量距离$b'$到向量$b$的距离最短（如下图所示）


如图所示，$OE=b',OD=b$,显而易见，$b'$是$b$向此二维平面的正交投影，此时$b'$和$b$之间的距离最近，距离差值维$DE$的长度。

而此时$b'=x_1*a_1+x_2*a_2=x_1OC+x_2OB$，$x_1,x_2$就是我们需要求出的值。

更进一步的理解。当有n组数据带入时，A矩阵的维度将会是n×2.那么这里整个最小二乘拟合问题就可以理解成：$a_1,a_2$是n维线性空间中的两个线性无关的向量，在span{$a_1,a_2$}所张成的子空间中(2维)找到$b$在其中的正交投影$b'$，二者之间的距离即是最小二乘优化的最小值min。$b'$在基$a_1,a_2$上的投影，即是要求解的变量值,

如果需要拟合的变量不止2个，假设有m个，那么整个问题就可以理解成是n维向量到m维超平面的正交投影求解。

回到公式（3）中来，对其的求解，有以下方法。

$$Ax=b \\ A^{T} A x=A^{T}b \\ x=(A^{T} A)^{-1}A^{T}b$$
按照道理来说，此时我们已经解决问题了。但是众所周知，对于高维度的矩阵，计算机进行求逆操作是非常慢的，问题就出在实际应用中，点云地面的拟合，可能是几千上万个点，这样就会导致A矩阵的维度很高，显然直接求逆操作在此时是不可行的。所以，如何快速求解$Ax=b$是下一个要解决的问题，即SVD分解。

2 实际问题1：点云的地面拟合

其算法理论基于论文:Zermas, D., Izzat, I., & Papanikolopoulos, N. (2017). Fast segmentation of 3D point clouds: A paradigm on LiDAR data for autonomous vehicle applications. Proceedings - IEEE International Conference on Robotics and Automation, 5067–5073. https://doi.org/10.1109/ICRA.2017.7989591

2.1 解法1.分解协方差矩阵

此方法来自论文。

对靠近地面的的n个点，计算其协方差矩阵。对协方差矩阵进行SVD分解，可以得到对应的特征值和特征向量。其中，最小特征值对应的特征向量就是地面平面的法向量。

求证：平面Ax+By+Cz+D=0的法向量为（A,B,C）.

证明：假设$(x_1,y_1,z_1),(x_2,y_2,z_2)$是当前平面上的两个点。

则有：$Ax_1+By_1+Cz_1+D=0$,$Ax_2+By_2+Cz_2+D=0$,所以两式相减，可得：

$A(x_1-x_2)+B(y_1-y_2)+C(z_1-z_2)=0$,即

$$> > \left[ \begin{matrix} A & B & C \end{matrix} \right] > > \left[ \begin{matrix}   (x_1-x_2) \\ (y_1-y_2) \\ (z_1-z_2)   \end{matrix}  \right] > > =0 > >$$
右边的矩阵表示平面上的任一点，且该式对平面上的任意两点都成立。

所以$n=(A,B,C)$即是所在平面的法向量。

拟合地面所在的方程Ax+By+Cz+d=0

1. 取n个z值最小的点，认为其是地面点

取n个地面点，计算这n个点的协方差矩阵$Cov$，然后对其做SVD分解，得到其在各个分量。最小奇异值所对应的向量便是地面的法向量$n$.

由前面的证明可知：$n=(A，B，C)$

1. 对n个靠近地面的点遍历加和，计算一个均值$\bar X=(\bar x,\bar y,\bar z)$。认为此均值带入地面所在方程
   $$A\bar x+B\bar y+C\bar z+D≈0 \\ 即：A\bar x+B\bar y+C\bar z≈-D$$

此时$-D$的值已知。

此时，均值$\bar X$因为是n个点的均值，默认是最靠近地面所在平面的点。其他所有的n个点，都可以认为更偏离所拟合的平面。即：

$$A\bar x+B\bar y+C\bar z+D \pm \delta≈0 \\ 即：A\bar x+B\bar y+C\bar z≈-D \pm \delta$$
因此，在对\velodyne_points中所有的topic进行筛选地面点的过程中，所有的点$X_i=(x_i,y_i,z_i)$带入式(3)所得到的值符合以下约束：
$$Ax_i+By_i+Cz_i \in [-D - \delta,-D+\delta]$$
此时，$\delta$的值需要自己设定，代表了对地面点的筛选条件。

2.2 解法2. SVD 求解Ax=0

此方法类似于二维平面的直线拟合。

假设我们有$n$个($n>>4$)靠近地面的点，现假设地面平面所在的方程为$ax+by+cz+d=0$。利用这$n$个点对该平面方程的参数进行拟合。原理与二维平面的直线拟合类似，这里不做过多推导。

带入$n$个点的坐标，可得：

$$\left\{ \begin{array}{l} ax_1+by_1+cz_1+d=0 \\ ax_2+by_2+cz_2+d=0 \\ ax_3+by_3+cz_3+d=0 \\ ...\\ ax_n+by_n+cz_n+d=0 \end{array} \right.$$

即可化为以下$Ax=0$的齐次方程组形式(超定方程)。

$$\left[ \begin{matrix} x_1 & y_1 & z_1 & 1 \\ x_2 & y_2 & z_2 & 1 \\ \ & \ ... \ & & \\ x_n & y_n & z_n & 1 \\ \end{matrix} \right]_{n*4} \left[ \begin{matrix} a \\ b \\ c \\ d \end{matrix} \right]_{4*1} =0$$
对矩阵$A$进行SVD即可得最后的结果。

问题：这种方法如何处理$[a \ b \ c \ d]$的尺度问题？

证明：SVD=最小二乘

$$DP_w=0 \\ 即Ax=0$$

下面以$Ax=0$这种更普遍的表达形式进行推导。

当$A_{m*n}$是一个超定方程的时候，此等式无解，因此需要取最小二乘的形式，即：

$$min ||Ax||_2^2 \\ =min \ (x^{T}A^{T}Ax）\\ sbj.||x||=1$$
已知:
$$A^{T}A=V \Lambda V^T \\ A=U \Sigma V^{T} ,A^T=V \Sigma^T U^T\\ U^TU=V^TV=I \\ $$
可得，$V=[v_0 \ v_1 \ ... \ v_n]_{n*n}$是$n$维空间里的标准正交基。所以$x_{n*1}$可以由此标准正交基构成，即：
$$x=k_0v_0+k_1v_1+...+k_nv_n=\sum_{i=0}^{n} k_iv_i \ ,x \in \mathbb R^{n}\\ sbj. \ ||x||=1$$
由公式(12)可知:
$$A^TA=V \Sigma^T U^T U \Sigma V^{T} \\ = V \Sigma^T \Sigma V^{T} \\ = V\left[ \begin{matrix} \sigma_{max}^2 & \ & \ \\ \ & \ddots & \ \\ \ & \ & \sigma_{min}^2 \end{matrix} \right]V^T \\ $$
将(13)(14)带入到(11)中，
$$min=x^T [v_0 \ ... \ v_n] \left[ \begin{matrix} \sigma_{max}^2 & \ & \ \\ \ & \ddots & \ \\ \ & \ & \sigma_{min}^2 \end{matrix} \right] \left[ \begin{matrix}v_0^T \\ ... \\ v_n^T \end{matrix} \right] x \\ =x^T [v_0 \ ... \ v_n] \left[ \begin{matrix} \sigma_{max}^2v_0^T & \ & \ \\ \ & \ddots & \ \\ \ & \ & \sigma_{min}^2v_n^T \end{matrix} \right]x \\ =x^T \left[ \begin{matrix} \sigma_{max}^2v_0v_0^T & \ & \ \\ \ & \ddots & \ \\ \ & \ & \sigma_{min}^2v_nv_n^T \end{matrix} \right]x \\ = x^T \left[ \begin{matrix} \sigma_{max}^2 & \ & \ \\ \ & \ddots & \ \\ \ & \ & \sigma_{min}^2 \end{matrix} \right]x \\ = x^T \left[ \begin{matrix} \sigma_{max}^2 & \ & \ \\ \ & \ddots & \ \\ \ & \ & \sigma_{min}^2 \end{matrix} \right]x \\ =[k_0v_0 \ ... \ k_nv_n]\left[ \begin{matrix} \sigma_{max}^2 & \ & \ \\ \ & \ddots & \ \\ \ & \ & \sigma_{min}^2 \end{matrix} \right] \left[ \begin{matrix} k_0v_0^T \\ ... \\ k_nv_n^T \end{matrix} \right] \\ =k_0^2\sigma_{max}^{2} + ...+k_n^2\sigma_{min}^{2} \\ 上述情况中，\mathrm{k}_{n}=1, \quad \mathrm{k}_{\mathrm{i}}(i \neq n)=0 \\ =\sigma_{min}^{2}$$
此时，対应$x=k_nv_n=v_n$

3 实际问题2：三角化

假设世界中的某点$P_w$（世界坐标未知）被连续n帧相机数据观测到，像素坐标分别是$(u_1,v_1),...,(u_n,v_n)$.n帧对应的相机坐标$T_{wc1},...,T_{wcn}$,皆已知。根据三角化，我们可以构建最小二乘表达式，综合$n$帧观测数据，获得点$P_w$的位置。

预备推导：

$Pci$:$P_w$在第$i$帧相机坐标系$T_{wci}$下的坐标。

$P_{ci}=T_{cwi}P_{w}$

$P_{w}=T_{wci}P_{ci} \\ \ \ \ \ \ =aa$

$P_{ci}=(x_{ci},y_{ci},z_{ci})=z_{ci}(\frac{x_{ci}}{z_{ci}},\frac{y_{ci}}{z_{ci}},1)=\lambda{i}(u_i,v_i,1)=\lambda_ip_i$

其中，$\lambda_i$是深度值，$p_i$是像素坐标

$$P_{w}=T_{wci}P_{ci} \\ P_{w}=T_{wci}\lambda_ip_i \\T_{ciw}P_w=\lambda_ip_i \\ $$

展开成矩阵的形式：

$$\lambda_i \left[ \begin{matrix} v_i \\ u_i \\ 1 \end{matrix} \right]_{3*1} = \left[ \begin{matrix}\left[ \begin{matrix} R_{cw} \end{matrix} \right]_{3*3}[t_{cw}]_{3*1} \end{matrix} \right]_{3*4}P_w \\ = \left[ \begin{matrix}\left[ \begin{matrix} R_{cw} \end{matrix} \right]_{3*3}[t_{cw}]_{3*1} \end{matrix} \right]_{3*4}\left[ \begin{matrix} x_w \\ y_w \\ z_w \\ 1 \end{matrix} \right]_{4*1} \\ = \left[ \begin{matrix} R_{11} & R_{12} & R_{13} & t_{1} \\ R_{21} & R_{22} & R_{23} & t_{2} \\ R_{31} & R_{32} & R_{33} & t_{3} \\ \end{matrix} \right]_{3*3} \left[ \begin{matrix} x_w \\ y_w \\ z_w \\ 1 \end{matrix} \right]_{4*1}$$
将其拆成行表示：
$$\lambda_{i} u_i= [R_{1} \ t_1]P_w=1*4 * 4*1 \\\lambda_{i} v_i= [R_{2} \ t_2]P_w=1*4 * 4*1 \\\lambda_{i} = [R_{3} \ t_3]P_w=1*4 * 4*1 \\ $$
这里一共有4个未知数，分别是$P_w$的3个和一个$\lambda_i$深度未知，将第三行带入到第一，二行，变成以下形式：
$$u_i[R_{3} \ t_3]P_w = [R_{1} \ t_1]P_w \\v_i[R_{3} \ t_3]P_w = [R_{2} \ t_2]P_w \\ $$

$$u_i[R_{3} \ t_3]P_w - [R_{1} \ t_1]P_w=0 \\v_i[R_{3} \ t_3]P_w - [R_{2} \ t_2]P_w=0 \\ $$

我的尼玛的！当然能化成Dy=0的形式。因为这是齐次方程组啊！这里左右都由x，是能单独提出来的。跟Ax=b带一个常数的形式是不一样的！傻逼！

即：

$$(u_i[R_{3} \ t_3] - [R_{1} \ t_1])_{1*4}P_w=0 \\ (v_i[R_{3} \ t_3] - [R_{2} \ t_2])_{1*4}P_w=0 \\ $$
因此，可以将(7)中括号部分视作矩阵$D_{2*4}$,即：
$$D_iP_w=0$$

注意D的维度是2×4，P是4×1，此时只是一组数据。所以当有n帧图像数据的时候，D的维度是2n×4.

接下来对D进行SVD分解

$$D^{T}D=U\Sigma V \\ =\sum_{i=1}^{4} \sigma_{i}^{2} \mathbf{u}_{i} \mathbf{u}_{j}^{\top} \\ 其中：D^T:4*2n, \\ D:2n*4. \\ U:4*4, \\ V:4*4, \\ \Sigma:4*4 \\ u_i:4*1, \\ u_j:1*4. \\ $$
结论：$\Sigma$是奇异值处于对角线上的奇异值矩阵。其最小奇异值对应的v即是要求的解。

SVD的计算方法：https://byjiang.com/2017/11/18/SVD/

4 实际问题3：图像压缩&数据压缩

参考资料：https://www.zhihu.com/search?type=content&q=SVD

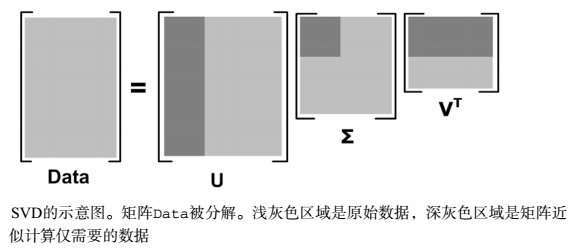
对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。

也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。

也就是说：

$$A_{m \times n}=U_{m \times m} \Sigma_{m \times n} V_{n \times n}^{T} \approx U_{m \times k} \Sigma_{k \times k} V_{k \times n}^{T}$$

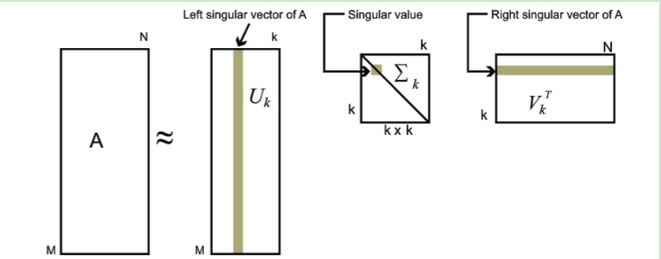
由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。

    Mat image = imread("/home/alex/Pictures/earth.jpg", 0);
    Mat temp(image.size(), CV_32FC1, Scalar(0));
    image.convertTo(image, CV_32FC1);
    Mat U, W, V;
    SVD::compute(image, W, U, V,4);//opencv得到的V已经经过转置了
    Mat w(image.rows, image.cols, CV_32FC1, Scalar(0));
    int k = 90;
    float radio = (float)(1920 * 1080) / (float)(k*(1920 + 1080 + 1));//1920k 1080k k  分别是 U的行数乘保留的列数 + k个特征值 +V的列数乘k行
    for (int i = 0; i < k; i++)
        w.ptr<float>(i)[i] = W.ptr<float>(i)[0];
    cout << "U = " << U.cols << " U = " << U.rows << endl;
    cout << "w = " << w.cols << " w = " << w.rows << endl;
    cout << "V = " << V.cols << " V = " << V.rows << endl;
    temp = U*w*V;
    image.convertTo(image, CV_8UC1);
    temp.convertTo(temp, CV_8UC1);
    namedWindow("src",WINDOW_NORMAL);
    namedWindow("res",WINDOW_NORMAL);
    imshow("src",image);
    imshow("res",temp);
    waitKey(0);
    cout << "k = " << k << ",\t" << "radio = " << radio << endl;

输出：

rows: 1920 cols:1080
U = 1920 U = 1920
w = 1080 w = 1920
V = 1080 V = 1080
k = 90, radio = 7.67744

对比如下：

原图:

PCA降维处理：

由此可以总结出：若一个像素为1字节, 原始图像需 字节的存储空间, 而使用SVD分解后只需 字节的存储空间, 以此达到压缩图像(矩阵)的目的.(k即是要保留的前k个最大的特征值)