最小二乘问题算法

robotics-algorithm

---

1 最小二乘

普通最小二乘法的推导证明
线性代数之矩阵求导
最小二乘法解的矩阵形式推导

不方便直接用非线性最小二乘方法求解的问题，使用迭代方式求解。

2 牛顿法

Newton's method in optimization wiki
Newton Method如何通俗易懂地讲解牛顿迭代法，牛顿法有一个问题就是初始点的选择必须满足一定条件。
python实现牛顿法求解求解最小值（包括拟牛顿法）

3 最速下降法

Gradient descent wiki
实践例子，梯度下降法及其Python实现，根据理解我实现了随机梯度下降法，并和批量梯度下降法做了比较。
梯度下降法，牛顿法，高斯-牛顿迭代法，附代码实现

批量梯度下降：
优点：全局最优解；易于并行实现；总体迭代次数不多
缺点：当样本数目很多时，训练过程会很慢，每次迭代需要耗费大量的时间。

随机梯度下降（SGD）：
优点：训练速度快，每次迭代计算量不大
缺点：准确度下降，并不是全局最优；不易于并行实现；总体迭代次数比较多。

这里的下降步长被简化成了一个固定值(学习率)，步长的选取是line search算法决定的。

4 line search 算法确定步长

line search python实现

4.1 Golden section method (exact method 精确解法)

见课本。

4.2 Armijo condition

Armijo condition事实上是下面的Wolfe condition的第一个条件。

4.3 Wolfe condition (inexact methods 非精确解法)

这个里面有一些代码细节没有看懂！！存疑先留着！！

Wolfe condition步长计算参考文章, $p_k$是下降方向，这篇文章讲得太赞了！一共有两个条件。

$$f(x_k+\alpha_k p_k)\le f(x_k)+c_1 \alpha_k \nabla f(x_k)^Tp_k \tag{1}$$

这个条件的意思是，除了要保证目标函数的要有所下降之外，还要保证下降的程度要和步长 $\alpha$ 成正比，这一点也可以从下图中看出来，可接受的$\alpha$ 必须要使得迭代点的函数值在虚线以下。这里注意，在实际中 $c_1$ 一般取一个较小的值，比如 $c_1=10^{-4}$。

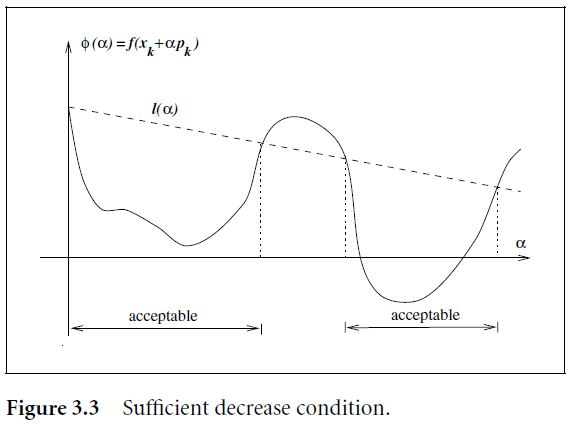
但光这一个条件还不能保证迭代点的正确收敛，因为从图中可以看出当 α 取很小的值时，这个条件就一定是满足的，因此，另一个条件从曲率（斜率）的角度进行了约束(curvature condition)：

$$f(x+\alpha_k p_k)^Tp_k\ge c_2\nabla f(x_k)^Tp_k \tag{2}$$

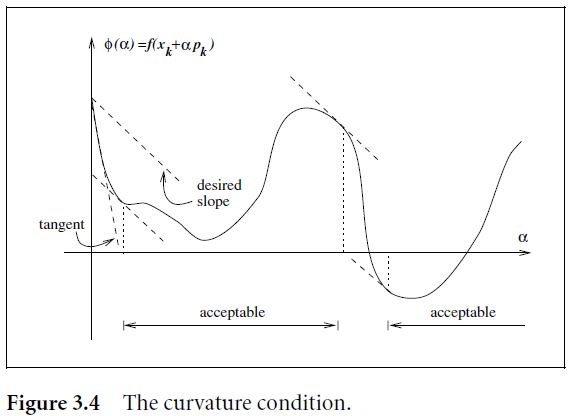
其中 $c_2\in(c_1,1)$。这个条件的意思是，在下一个迭代点处的斜率一定要大于在当前点（$\alpha=0$）处的斜率。因为我们可以看出来，上面这个条件的左面是以 $\alpha$为变量的函数在下一个迭代点出的导数，而右边则是其在当前迭代点的导数。上面的这个条件可以从下图中进行理解。

其实也可以这样理解，当某个 $\alpha$ 的取值使得在该点 $\phi(\alpha)$ 的导数很小（绝对值很大）时，就表示目标函数还有下降的可能因此不能在这儿停，知道导数变大趋于0，甚至变成正值（在往上走了），说明可能就要停下来了。

5 高斯牛顿法

Gauss–Newton algorithm wiki
Gauss-Newton推导

the Gauss–Newton algorithm can only be used to minimize a sum of squared function values, but it has the advantage that second derivatives, which can be challenging to compute, are not required.
高斯 - 牛顿算法只能用于最小化平方函数值的总和，但它具有的优点是不需要可能难以计算的二阶导数。

6 阻尼牛顿法（LMA）

Levenberg–Marquardt algorithm wiki
如何理解拉格朗日乘子法？