Bayes Filter推导

navigation-algorithm

---

1 Basic Knowledge

• Multivariate normal distributions are characterized by PDF of the following form
  $$p(x)=\operatorname{det}(2 \pi \Sigma)^{-\frac{1}{2}} \exp \left\{-\frac{1}{2}(x-\mu)^{T} \Sigma^{-1}(x-\mu)\right\}$$
• If $X$ and $Y$ are independent, we have
  $$p(x, y)=p(x) p(y)$$
• Conditional probability are described as
  $$p(x | y)=\frac{p(x, y)}{p(y)}$$
• If $X$ and $Y$ are independent, we have
  $$p(x | y)=\frac{p(x, y)}{p(y)}=\frac{p(x) p(y)}{p(y)}=p(x)$$
• Total probability
  $$p(x)=\sum_{y} p(x | y) p(y) \quad$$

• Conditional probability with total probability
  

  $$p(x | y)=\frac{p(y | x) p(x)}{p(y)}=\frac{p(y | x) p(x)}{\sum_{x^{\prime}} p\left(y | x^{\prime}\right) p\left(x^{\prime}\right)} \quad$$
  An important observation is that the denominator of Bayes rule, $p(y)$, does not depend on $x$. Thus, the factor $p(y)$ will be the same for any value $x$ in the posterior $p(x | y)$. For this reason, $p(y)$ is often written as a normalizer in Bayes rule variable, and generically denoted $\eta$
  $$p(x | y)=\eta p(y | x) p(x)$$

• Conditional independence
  

  $$p(x, y | z)=p(x | z) p(y | z)$$
  is equivalent to
  $$\begin{array}{l}{p(x | z)=p(x | z, y)} \\ {p(y | z)=p(y | z, x)}\end{array}$$
  but
  $$p(x, y | z)=p(x | z) p(y | z) \quad \not=\quad p(x, y)=p(x) p(y)$$
  $$p(x, y)=p(x) p(y) \quad \not=\quad p(x, y | z)=p(x | z) p(y | z)$$

• The expectation of a random variable $X$ is given by
  $$E[X]=\sum_{x} x p(x) \quad(\text { discrete })$$
  $$E[a X+b]=a E[X]+b$$
• The covariance of X is obtained as follows
  $$\operatorname{Cov}[X]=E[X-E[X]]^{2}=E\left[X^{2}\right]-E[X]^{2}$$
• Entropy
  $$H_{p}(x)=E\left[-\log _{2} p(x)\right]$$
  which resolves to
  $$H_{p}(x)=-\sum_{x} p(x) \log _{2} p(x) \quad(\text { discrete })$$

2 Mathematical Derivation of the Bayes Filter

• Environment measurement data
  The notation
  $$z_{t_{1} : t_{2}}=z_{t_{1}}, z_{t_{1}+1}, z_{t_{1}+2}, \dots, z_{t_{2}}$$
  denotes the set of all measurements acquired from time $t_1$ to time $t_2$ , for $t_1 \leq t_2$
• Control data
  As before, we will denote sequences of control data by $u_{t_1 :t_2}$ , for $t_1 \leq t_2$
  $$u_{t_{1} : t_{2}}=u_{t_{1}}, u_{t_{1}+1}, u_{t_{1}+2}, \dots, u_{t_{2}}$$
• An important insight
  $$p\left(x_{t} | x_{0 : t-1}, z_{1 : t-1}, u_{1 : t}\right)=p\left(x_{t} | x_{t-1}, u_{t}\right)$$
  $$p\left(z_{t} | x_{0 : t}, z_{1 : t-1}, u_{1 : t}\right)=p\left(z_{t} | x_{t}\right)$$

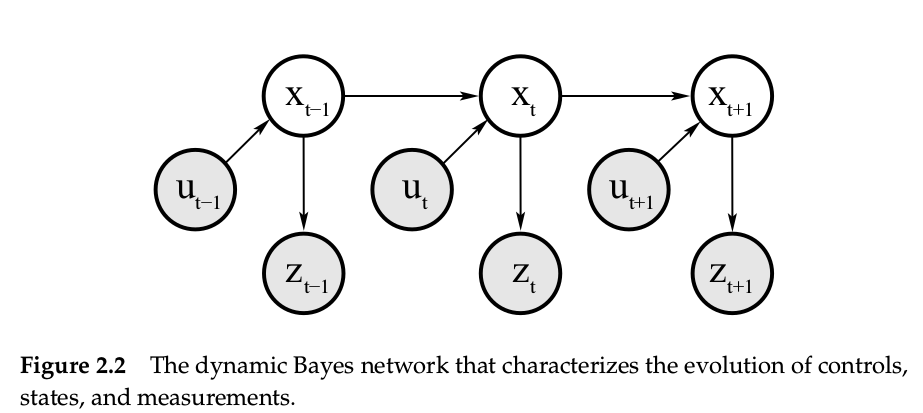
- Belief Distributions

$$\operatorname{bel}\left(x_{t}\right)=p\left(x_{t} | z_{1 : t}, u_{1 : t}\right)$$
$$\overline{b e l}\left(x_{t}\right)=p\left(x_{t} | z_{1 : t-1}, u_{1 : t}\right)$$

• The Bayes Filter Algorithm
  
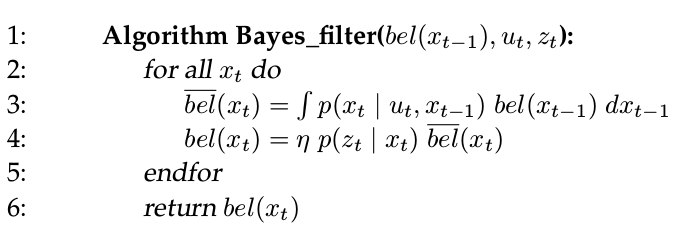
  target posterior
  $$\begin{aligned} p\left(x_{t} | z_{1 : t}, u_{1 : t}\right) &=\frac{p\left(z_{t} | x_{t}, z_{1 : t-1}, u_{1 : t}\right) p\left(x_{t} | z_{1 : t-1}, u_{1 : t}\right)}{p\left(z_{t} | z_{1 : t-1}, u_{1 : t}\right)} \\ &=\eta p\left(z_{t} | x_{t}, z_{1 : t-1}, u_{1 : t}\right) p\left(x_{t} | z_{1 : t-1}, u_{1 : t}\right) \end{aligned}$$
  conditional indepen-dence
  $$p\left(z_{t} | x_{t}, z_{1 : t-1}, u_{1 : t}\right)=p\left(z_{t} | x_{t}\right)$$
  simplify as follows
  $$p\left(x_{t} | z_{1 : t}, u_{1 : t}\right)=\eta p\left(z_{t} | x_{t}\right) p\left(x_{t} | z_{1 : t-1}, u_{1 : t}\right)$$

$$\begin{aligned} \overline{\operatorname{bel}}\left(x_{t}\right) &=p\left(x_{t} | z_{1 : t-1}, u_{1 : t}\right) \\ &=\int p\left(x_{t} | x_{t-1}, z_{1 : t-1}, u_{1 : t}\right) p\left(x_{t-1} | z_{1 : t-1}, u_{1 : t}\right) d x_{t-1} \end{aligned}$$
$$p\left(x_{t} | x_{t-1}, z_{1 : t-1}, u_{1 : t}\right)=p\left(x_{t} | x_{t-1}, u_{t}\right)$$
$$\overline{b e l}\left(x_{t}\right)=\int p\left(x_{t} | x_{t-1}, u_{t}\right) p\left(x_{t-1} | z_{1 : t-1}, u_{1 : t-1}\right) d x_{t-1}$$