Ceres Tutotial（2） —— 最小二乘建模

Optimization

写在前面

8.9 关于添加残差块，参数块，设置参数化的区别和调用关系【重要】

这一节相当重要，尤其是写代码的时候。

1 CostFunction和SizedCostFunction

在旧版本的ceres里面，参数块最大是10个，但是新版本的ceres使用了可变长模板参数，所以参数快数量不限制。

1.1 细节对比

CostFunction的存在是为了计算残差和雅克比矩阵。
主要接口。

class CostFunction {
 public:
  virtual bool Evaluate(double const* const* parameters,
                        double* residuals,
                        double** jacobians) = 0;
  const vector<int32>& parameter_block_sizes();
  int num_residuals() const;
 protected:
  vector<int32>* mutable_parameter_block_sizes();
  void set_num_residuals(int num_residuals);
};

• 使用解析求导的时候，构建costfunction，除了之前的例子继承SizedCostFunction之外，也可以继承CostFunction
• 继承SizedCostFunction，可以在继承的时候在模板参数指定残差和参数块维度

class AnalyticCostFunction
    : public ceres::SizedCostFunction<1 /* number of residuals */,
                                      2 /* size of first parameter */> 
{
    ...
}

• 继承SizedCostFunction，需要通过继承的成员函数set_num_residuals和mutable_parameter_block_sizes设置残差和参数块维度

class AnalyticCostFunction2
        : public ceres::CostFunction {
public:
    AnalyticCostFunction2(const int& num_residuals, const int& block_sizes,
            double x, double y) : x_(x), y_(y) {
        set_num_residuals(num_residuals); // 设置残差维度
        std::vector<int>* param_block_sizes = mutable_parameter_block_sizes(); // 返回的引用
        param_block_sizes->push_back(block_sizes); // 设置参数块维度，有几个参数块，就pubsh_back几次
    }
    ...
}
// 使用
CostFunction *cost_function = new AnalyticCostFunction2(1,2,data[2*i], data[2*i + 1]);
problem.AddResidualBlock(cost_function, NULL, x);

其实通过查看SizedCostFunction也是继承了CostFunction的， 通过查看其构造函数可以发现我们刚才直接继承CostFunction构建functor的方法其实和SizedCostFunction是一样的。
只不过Ceres已经帮我们做好了，以后我们只使用SizedCostFunction就好了，很方便。

  SizedCostFunction() {
    set_num_residuals(kNumResiduals);
    *mutable_parameter_block_sizes() = std::vector<int32_t>{Ns...};
  }

1.2 两种定义cost function的完整代码对比

//-------------------------------------------
// 解析求导方式1
//-------------------------------------------
class AnalyticCostFunction
        : public ceres::SizedCostFunction<1 /* number of residuals */,
                2 /* size of first parameter */> {
public:
    AnalyticCostFunction(double x, double y) : x_(x), y_(y) {}
    virtual ~AnalyticCostFunction() {}
    /**
     * @brief 重载Evaluate函数，完成jacobian和residuals的计算
     * @param parameters
     * @param residuals
     * @param jacobians
     * @return
     */
    virtual bool Evaluate(double const *const *parameters,
                          double *residuals,
                          double **jacobians) const {
        double m = parameters[0][0]; // parameters[0]表示取出第一组参数
        double c = parameters[0][1];
        // 计算残差
        residuals[0] = y_ - exp(m*x_ + c);
        // 计算雅克比
        if (jacobians != NULL && jacobians[0] != NULL) {
            jacobians[0][0] = -x_*exp(m*x_ + c);
            jacobians[0][2] = -exp(m*x_ + c);
        }
        return true;
    }
private:
    const double x_;
    const double y_;
};
//-------------------------------------------
// 解析求导方式2
//-------------------------------------------
class AnalyticCostFunction2
        : public ceres::CostFunction {
public:
    AnalyticCostFunction2(const int& num_residuals, const int& block_sizes,
            double x, double y) : x_(x), y_(y) {
        set_num_residuals(num_residuals); // 设置残差维度
        std::vector<int>* param_block_sizes = mutable_parameter_block_sizes(); // 返回的引用
        param_block_sizes->push_back(block_sizes); // 设置参数块维度，有几个参数块，就pubsh_back几次
    }
    virtual ~AnalyticCostFunction2() {}
    /**
     * @brief 重载Evaluate函数，完成jacobian和residuals的计算
     * @param parameters
     * @param residuals
     * @param jacobians
     * @return
     */
    virtual bool Evaluate(double const *const *parameters,
                          double *residuals,
                          double **jacobians) const {
        double m = parameters[0][0]; // parameters[0]表示取出第一组参数
        double c = parameters[0][3];
        // 计算残差
        residuals[0] = y_ - exp(m*x_ + c);
        // 计算雅克比
        if (jacobians != NULL && jacobians[0] != NULL) {
            jacobians[0][0] = -x_*exp(m*x_ + c);
            jacobians[0][4] = -exp(m*x_ + c);
        }
        return true;
    }
private:
    const double x_;
    const double y_;
};

2 AutoDiffCostFunction

使用自动求导应该注意的地方，比如下面的例子。

自动求导设置参数维度的时候，一定要注意。有几个参数就必须写几个参数块，对于非线性的参数不能合并到一起。还是看代码比较清晰。

当然，如果你使用解析求导，随便你怎么写啦，因为求导是你自己定义的呢。这块具体为什么，参看自动求导的原理。

// 定义
struct ExponentialResidual {
    ExponentialResidual(double x, double y)
            : x_(x), y_(y) {}
    // ------------【正确写法】------------
    template<typename T>
    bool operator()(const T *const m,
                    const T *const c,
                    T *residual) const {
        residual[0] = y_ - exp(m[0]*x_ + c[0]);
        return true;
    }
    // ------------【错误写法】------------
//    template<typename T>
//    bool operator()(const T *const x,
//                    T *residual) const {
//        residual[0] = y_ - exp(x[0]*x_ + x[1]);
//        return true;
//    }
private:
    const double x_;
    const double y_;
};
// 使用
// ------------【正确写法】------------
problem.AddResidualBlock(
        new AutoDiffCostFunction<ExponentialResidual, 1, 1, 1>(
                new ExponentialResidual(data[2*i], data[2*i + 1])),
        NULL,
        &m, &c);
// ------------【错误写法】------------
//        problem.AddResidualBlock(
//                new AutoDiffCostFunction<ExponentialResidual, 1, 2>(
//                        new ExponentialResidual(data[2*i], data[2*i + 1])),
//                NULL,

3 其他cost function

这些不常用，用的时候，具体参看官方文档。

• DynamicAutoDiffCostFunction
  AutoDiffCostFunction要求在编译时知道参数块的数量及其大小。在许多应用中，这还不够，例如Bezier曲线拟合，神经网络训练等。
• NumericDiffCostFunction 和 DynamicNumericDiffCostFunction
• CostFunctionToFunctor 和 DynamicCostFunctionToFunctor
  CostFunctionToFunctor是一个适配器类，允许用户在template functors中使用CostFunction对象，该函子将用于自动求导。 这使用户可以无缝地混合使用分析，数值和自动求导三种方式。
• ConditionedCostFunction
  此类允许您对包装成本函数的残值应用不同的条件。 有一个有用的例子是，您已有一个产生N个值的成本函数，但您希望总成本不只是这些平方值的总和-也许您想对某些值应用不同的缩放比例， 改变他们对成本的贡献。

4 用法不清楚的模块

• GradientChecker
  doc 参考
  貌似是用来验证雅克比的，还不清楚用法，验证程序还不对，先留坑。。。。。
• NormalPrior
  doc 参考

5 LossFunction

设置核函数，抑制outliers影响。

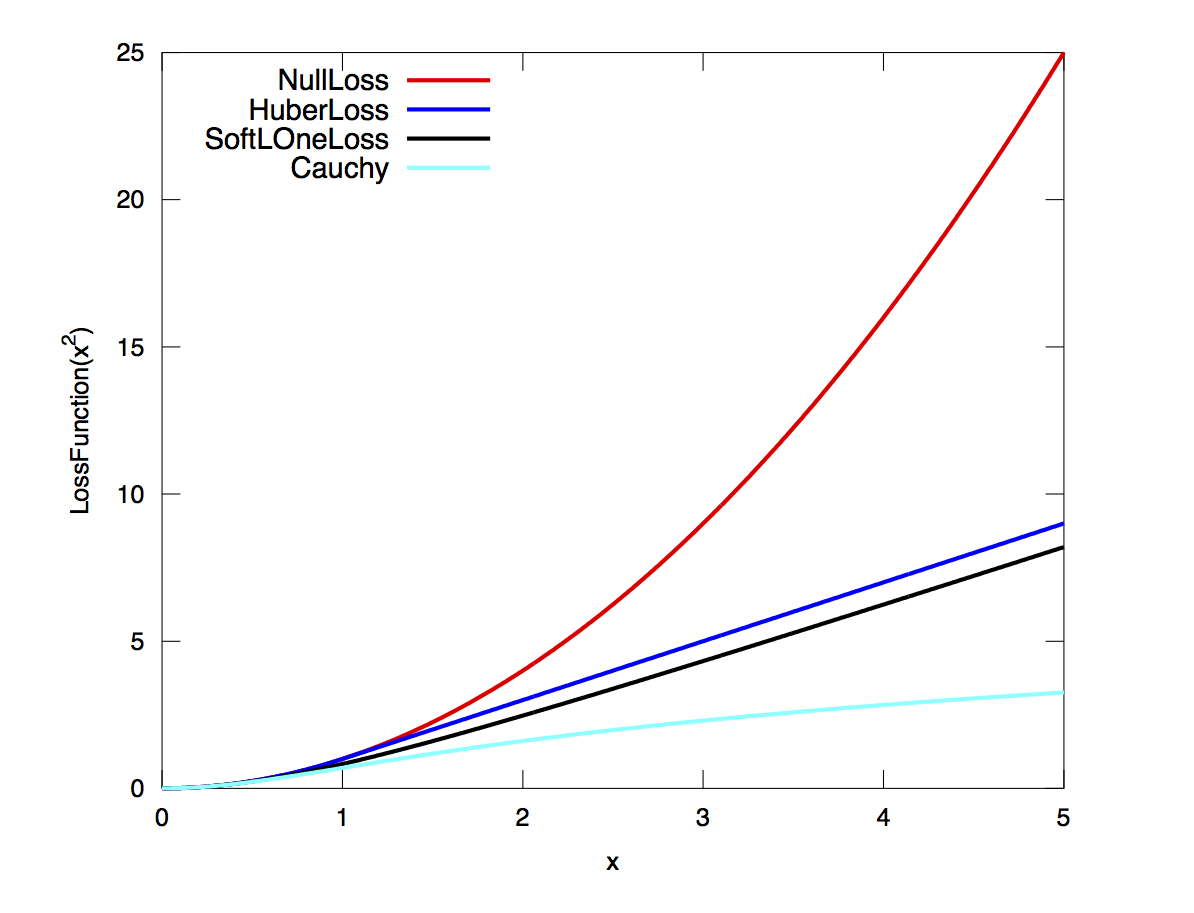
• ComposedLoss组合损失函数
• ScaledLoss 缩放损失函数
• LossFunctionWrapper 可变损失函数
  eg：求解问题分为两步，先大尺度，后小尺度

Problem problem;
// Add parameter blocks
CostFunction* cost_function =
    new AutoDiffCostFunction < UW_Camera_Mapper, 2, 9, 3>(
        new UW_Camera_Mapper(feature_x, feature_y));
LossFunctionWrapper* loss_function(new HuberLoss(1.0), TAKE_OWNERSHIP);
problem.AddResidualBlock(cost_function, loss_function, parameters);
Solver::Options options;
Solver::Summary summary;
Solve(options, &problem, &summary);
loss_function->Reset(new HuberLoss(1.0), TAKE_OWNERSHIP);
Solve(options, &problem, &summary);

6 LocalParameterization

使用情况：

• 过参数化，比如四元数，传入参数是4个，实际参数是3个
• 其他空间上更新参数，eg：manifold space，tangent space

该类的内部主要接口

class LocalParameterization {
 public:
  virtual ~LocalParameterization() {}
  // override Plus()函数进行更新
  virtual bool Plus(const double* x,
                    const double* delta,
                    double* x_plus_delta) const = 0;
  virtual bool ComputeJacobian(const double* x, double* jacobian) const = 0;
  virtual bool MultiplyByJacobian(const double* x,
                                  const int num_rows,
                                  const double* global_matrix,
                                  double* local_matrix) const;
  // GlobalSize()返回参数块大小，eg：四元数返回4
  virtual int GlobalSize() const = 0;
  // LocalSize()返回参数块在对应空间的实际大小，eg，四元数返回3
  virtual int LocalSize() const = 0;
};

重新写一个类，继承LocalParameterization

ceres也为我们写好了一部分例子，可以直接拿来用，参考

7 AutoDiffLocalParameterization

对应的自动求导里面也有过参数过的处理形式，自定义更新形式，参考

8 Problem

ceres最核心的模块，用于构建最小二乘问题的关键。

8.1 添加残差块

8.1.1 简介

Problem::AddResidualBlock() 意思如同他的名字一样，向最小二乘问题添加一个参数块。具体包括

• CostFunction 代价函数，携带了参数块和残差块的size信息
• LossFunctio 核函数，不用的话可设为NULL。
• 参数1,参数2...

该函数会检查传入的CostFunction中size和实际列表中的参数size是否一致。

8.1.2 两种调用接口

8.2 添加参数块

8.2.1 简介

用户可以使用以下选项显式添加参数块，Problem::AddParameterBlock()。
实际上，Problem::AddResidualBlock()隐式地添加不存在的参数块，所以不需要显式地调用Problem::AddParameterBlock()。

• LocalParameterization情况
  AddParameterBlock()还允许用户将LocalParameterization对象与参数块关联。具有相同参数的重复调用将被忽略（忽略默认的那个调用）。使用相同的双指针但大小不同的重复调用将导致未定义的行为。
• 设置const参数块
  可以使用Problem::SetParameterBlockConstant()将任何参数块设置为常量，然后使用SetParameterBlockVariable()撤消此操作。

8.2.2 两种调用接口

第一个可以添加局部参数化的更新方法，用于过参数或者manifold space参数更新。
第二个则是使用默认的参数更新plus方法。

8.3 删除残差块

void Problem::AddParameterBlock(double *values, int size)
void Problem::RemoveResidualBlock(ResidualBlockId residual_block)

删除残差或参数块将破坏隐式排序，导致从求解器返回的雅可比矩阵或残差无法解释。如果依赖于求值的雅可比矩阵，不要使用remove!在将来的版本中可能会有所改变。在优化过程中保持指定的参数块不变。

8.4 设置参数块为常量或者变量

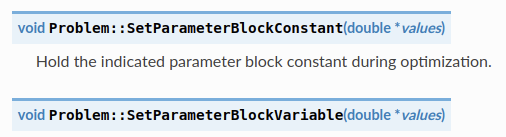
在优化过程中保持指定的参数块不变。
或者
允许指定的参数在优化期间发生变化。

8.5 设置参数块的参数化方式

当然也可以获取参数的参数化方式

LocalParameterization *Problem::GetParameterization(double *values) const

获取与此参数块关联的本地参数化对象。 如果没有关联的参数化对象，则返回NULL

8.6 设置参数的上下边界

void Problem::SetParameterLowerBound(double *values, int index, double lower_bound)
void Problem::SetParameterUpperBound(double *values, int index, double upper_bound)

默认上下边界为无穷。

8.7 获取Problem内部情况的接口函数

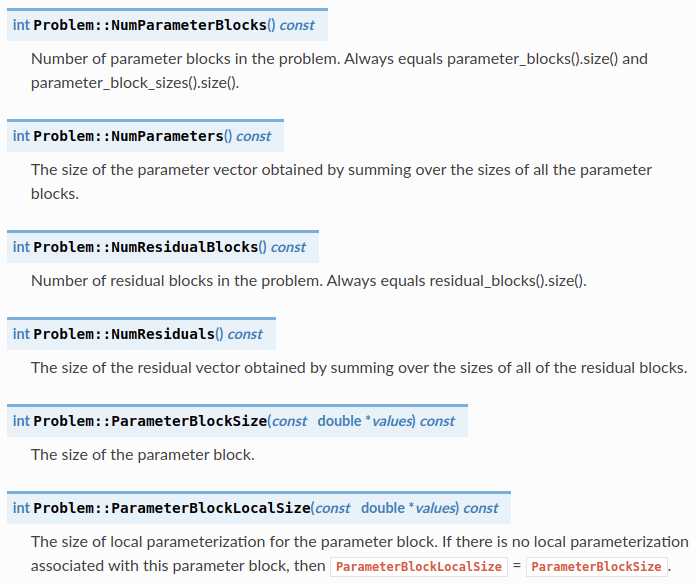
8.8 Evaluate相关

参看文档

8.9 关于添加残差块，参数块，设置参数化的区别和调用关系【重要】

通过查看源代码，分析出了这三个模块的调用关系。之所以会关注这个问题，起初是因为在VINS-MONO中优化的函数中关于添加各种残差和添加参数块，有的残差块添加了对应的参数块，有的没有，不知所以然。所以研究一下ceres源代码。哈哈，套用侯捷老师一句话

我们这里探讨的主要是应用在解析求导的时候，过参数，manifold space情况下(eg: 四元数)，针对我们的参数更新，应该使用自定义的方法。主要通过AddParameterBlock和SetParameterization来实现。

源码面前，了无秘密！ —— 侯捷

• AddResidualBlock
• AddParameterBlock
• SetParameterization

经过前面的介绍，做优化的第一步就是构建对应的CostFunction，完事后，调用AddResidualBlock函数添加残差块，这个函数里面事实上会调用AddParameterBlock函数，而AddParameterBlock函数里面实际上会调用SetParameterization函数。

也就是说如果我们的参数属于正常的plus更新的话，也就是没有过参数，没有manifold space，那么就完全不需要调用AddParameterBlock或者SetParameterization函数

如果我们的参数需要自定义更新方式，我们可以调用AddParameterBlock或者SetParameterization函数任何一个都可以，调用方式如下

// 方法1
void AddParameterBlock(double* values,
                     int size,
                     LocalParameterization* local_parameterization);
// 方法2
void SetParameterization(double* values,
                       LocalParameterization* local_parameterization);

这里提一下既然程序中给了默认的参数化方法，我们自己添加的话，程序就会调用我们的自定义方法。
还有一个比较有意思的地方是程序虽然反复调用了AddParameterBlock，但是参数并不会添加重复，因为内部使用map管理，每次添加的时候，都会保证地址不重复。

总结一下

• 参数正常更新，只需要调用AddResidualBlock
• 参数自定义更新，需要调用AddParameterBlock或者SetParameterization，要注意，数量一定要添加对，因为比如vins-mono里面参数非常多，搞不清楚参数维度就会很容易出错。

9 旋转相关