NDT Paper Reading

pcl

---

Abstract

对原始采样点云进行应用NDT算法之后，可以将扫描到的表面使用一个光滑的函数，这个函数有可解析的一阶导数和二阶导数。这样的表示方法有一些比较好的特性可以利用,它使得可以利用标准优化方法，如：牛顿法，进行scan registration。这个算法将2d registration扩展到3d， 并进行了一些提升。

使用技术，克服了普通registration算法中的离散表示问题：

• multiresolution discretisation
• trilinear interpolation

相比于icp算法，ndt对于比较差的initial pose估计更加快速，精确，鲁棒。

更进一步，提出了kernel-based extension 3d NDT算法用于注册coloured data。

• original algorithm 对于每一个quantum of space使用one metric normal distribution
• colour-NDT使用三个components，每一个使用一种颜色。这种表示允许仅有少量geometric features的coloured scans可以被注册。当3d点和图像数据都可以获得，使用图像数据的lcoal visual freatures进行scan registration是可能的。然后基于local features的方法通常只是用获得的3d点中的一小部分用于注册。相反，colured-NDT使用所有获得的3d点。

这篇论文提出结合使用local visual features和colourNDT的方法，在存在强重复纹理或扫描之间的动态变化的情况下，对彩色3D点云进行稳健配准。
同样基于NDT，提出了一种使用3D激光扫描为移动机器人执行基于外观的回环检测的新方法。
使用3d方法的两个难题：

• 如何处理大量数据
• 如何有效获得3d旋转不变性

所提出的方法仅使用3D点云的外观来检测循环并且不需要pose信息，它利用NDT表面表示来创建基于局部表面方向(local surface orientation)和平滑度(smoothness)的特征直方图(features histogram)。

• 表面形状直方图将输入数据压缩两到三个数量级。由于高压缩率，可以有效地匹配直方图以比较两次扫描的外观。
• 通过align扫描到的主要表面取向，来实现旋转不变性。

Chapter 1 Introduction

使用NDT后，扫描的表面使用具有一阶和二阶解析导数的光滑连续函数来表示，这样的表示有几种优势。
当执行3D成像时，通常情况是在单次扫描中不能捕获整个感兴趣区域;是因为遮挡，因为它太大，或者因为有问题的对象本身就是碎片。因此，通常需要执行3D扫描配准，以便生成完整的模型。为了对齐分段扫描（解决拼图游戏，可以这么说），有必要找到每次扫描的正确position和orientation; 就是它的pose。

1.1 Contributions

• 3D-NDT surface representation
• 3D-NDT registration with extensions
  通过使用多分辨率离散化技术和三线性插值，可以克服基本3D-NDT配准算法中存在的一些离散化问题
• Colour-NDT registration
• Appearance-based loop detection from 3D laser scans
• Boulder detection from 3D laser scans

Chapter2 Common concepts

2.1 rotation

NDT中使用欧拉角zyx来表示，在这种情况下使用欧拉角的基本原理是避免在数值优化方法中加入非线性约束。对于执行扫描配准时遇到的相对较小的角度，不太可能发生万向节锁定。因此，通过更容易的问题公式来评估欧拉角的潜在缺点。

2.2 registration

当两帧scans匹配上了，称为in registration。如何决定registration的ground truth的问题会在chapter6讨论。
局部的registration需要一个比较近的初始值，如果离得太远，则无法进行很好的匹配，这和global的registration不同。
scan registration的应用：

• pose tracking，机器人定位
• modelling（三维重建），比如矿井下的map

2.3 sampling

在许多情况下，尤其是在走廊和隧道中进行扫描时，扫描仪位置附近的点分布比远处更密集。如果以均匀随机的方式对点进行采样，则采样的子集将具有类似的不均匀分布。从扫描的远端的重要几何结构中取样会很少或没有点，会导致配准不好。

为了克服这个问题，通常使用某种形式的空间分布式采样，以确保样本密度在整个扫描体积上均匀。

在当前工作中完成此操作的方式是通过创建具有相同大小的单元格的网格结构并将扫描点放置在相应的单元格中。该采样网格的单元尺寸通常在0.1和0.2米之间。从随机单元格中抽取随机点，直到达到所需的点数。如果cell分布足够，这种策略将给出均匀的点分布。

2.4 slam

slam主要的step：

• registration,
• pose-covariance estimation,
• loop detection,
• relaxation.

registrater机器人的连续视图以跟踪机器人的pose（localization）并构建metric map（mapping）。对于每个视图（或从一组视图生成的submaps），将node插入到scene graphe中，其edge将当前submap连接到其neighbours。还需要估计相邻submaps之间的相对pose的covariance，并将其附加到edge of graph。 一旦机器人检测到它已返回到先前访问过的位置，就可以计算在遍历回环上累积的error。基于与每个edge相关联的covariance估计，通过执行relaxation of the graph，将地图重新形成为consistent state。

Chapter3 Range sensing

通常，较短的波长导致更高的距离分辨率（更准确的范围读数）和更少的镜面反射（从发光表面读取的读数更少），但由于吸收和散射（衰减）而导致更短的最大范围。 空气中的气体和颗粒吸收并散射能量，使得较少的光束返回到接收器，从而降低了测量的可靠性。

• radar
  因为雷达使用相对较长的波长，所以它可以在很长的范围内使用，尽管与波长较短的传感器相比分辨率较差。 此外，雷达不易受到灰尘，雾，雨，雪，真空或光线条件变化的影响。 雷达的一个独特功能是它可以检测多个物体向下范围。 然而，它不会穿透钢铁或坚硬的岩石
• lidar
  与雷达和声纳的光束相比，激光束可以高度聚焦，没有旁瓣。 这也是短波长的影响。
  与雷达相比，激光传感器的主要缺点是在扫描多尘或有雾环境时对衰减和散射的敏感性，尽管红外激光在穿透烟雾和灰尘方面比可见光更好。
  最近的激光雷达设备可以测量每个光束的多个回波，因此可以测量灰尘和超出它的表面。
  可以使用三角测量或通过测量发射光束的飞行时间或其相移来测量到物体的距离;
  
  • Triangulation
  • time of flight
• sonar
• steroeo vision
• Time-of-flight cameras

Chapter5 Related work on scan registration

点云匹配算法有很多种，下面的是一些经典算法

• ICP
• IDC
• PIC
• Point-based probabilistic registration
• NDT
• Gaussian fields
• Quadratic patches
• Likelihood-field matching
• CRF matching
• Branch-and-bound registration
• Registration using local geometric features

Chapter6 The normal-distributions transform

6.1 NDT for representing surfaces

但是，使用点云来表示曲面有许多限制。例如，点云不包含有关表面特征的明确信息，例如方向，平滑度或孔。根据传感器配置，点云也可能效率低下，需要不必要的大量存储。 为了获得远离传感器位置的足够的sample resolution，通常需要以从传感器附近的表面产生大量冗余数据的方式配置传感器。

NDT是一种method for representing a surface。
它首先由Biber和Straßer于2003年7提出，作为2D扫描配准的方法。 Biber和Straßer后来在与Sven Fleck 8的联合论文中详细阐述了该方法，同样在扫描配准和映射的背景下。

NDT的这种transform的核心思想是将点云映射到平滑表面来表示，使用一组局部概率密度函数（PDF）来描述，每个PDF描述表面的一部分的形状。

该算法的第一步是将扫描所占用的空间细分为单元网格（2D情况下的正方形或3D中的立方体），基于cell内的点的分布计算每个cell的PDF。

每个cell中的PDF可以被解释为cell内表面点$\vec{x}$的generative process（生成过程）。 换句话说，假设可以通过对该cell内点的分布的刻画来生成$\vec{x}$的位置。

假设参考扫描表面点 surface point的位置是由D-dimensional normal random process(D维正态随机过程)产生的，则测量得到$\vec{x}$的概率是

$p(\vec{x})=\frac{1}{(2 \pi)^{D / 2} \sqrt{|\mathbf{\Sigma}|}} \exp \left(-\frac{(\vec{x}-\vec{\mu})^{\mathrm{T}} \boldsymbol{\Sigma}^{-1}(\vec{x}-\vec{\mu})}{2}\right)$
其中 $\left((2 \pi)^{D / 2} \sqrt{|\boldsymbol{\Sigma}|}\right)^{-1}$可以用一个常数$c_0$来表示。均值和方差使用下面的公式来计算
$\begin{aligned} \vec{\mu} &=\frac{1}{m} \sum_{k=1}^{m} \vec{y}_{k} \\ \boldsymbol{\Sigma} &=\frac{1}{m-1} \sum_{k=1}^{m}\left(\vec{y}_{k}-\vec{\mu}\right)\left(\vec{y}_{k}-\vec{\mu}\right)^{\mathrm{T}} \end{aligned}$
其中$\vec{y}_{k=1, \dots, m}$是cell中point的位置。

正态分布给出了点云的分段平滑表示，具有连续导数。每个PDF都可以看作是局部表面的近似值，描述了表面的位置及其方向和平滑度。 2D激光扫描及其相应的正态分布如下图所示。 下下图显示了矿井隧道扫描的3D正态分布。

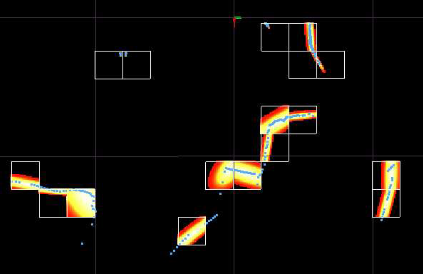
来自矿井隧道的2D激光扫描（显示为点）和描述表面形状的PDF。 在这种情况下，每个cell是边长为2米的正方形。 更亮的区域代表更高的概率。 仅针对超过五个点的cell计算PDF。

从上方看到的隧道剖面的3D-NDT表面表示。 更明亮，更密集的部分代表更高的概率。 cell的边长为1米。

由于目前的工作主要集中在正态分布上，让我们更仔细地研究单变量和多变量正态分布的特征。在一维情况下，正态分布的随机变量$x$具有一定的期望值$\mu$，并且关于该值的不确定性用方差$\sigma$表示，相当于维度$D=1$。
$p(x)=\frac{1}{\sigma \sqrt{2 \pi}} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right)$
这是多变量的正态分布表示，
$p(\vec{x})=\frac{1}{(2 \pi)^{D / 2} \sqrt{|\mathbf{\Sigma}|}} \exp \left(-\frac{(\vec{x}-\vec{\mu})^{\mathrm{T}} \boldsymbol{\Sigma}^{-1}(\vec{x}-\vec{\mu})}{2}\right)$

协方差矩阵的对角元素表示每个变量的方差variance，而非对角元素表示对应两个变量的协方差covariance。
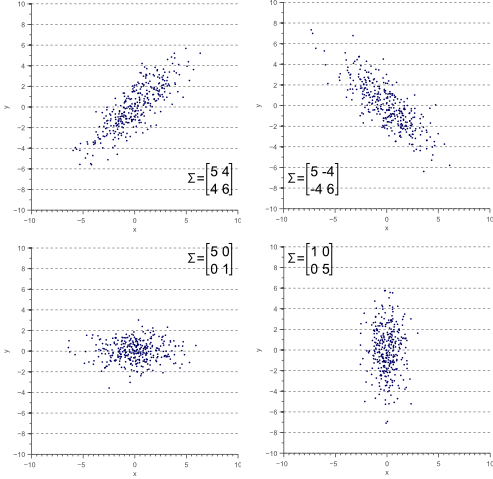
下图显示了三种不同维度的正态分布情况，

在2D和3D情况下，可以从协方差矩阵的特征向量和特征值来评估表面取向orientation和平滑度smoothness。 特征向量描述了分布的主要组成部分; 也就是说，一组正交矢量对应于变量的协方差的主导方向。

根据方差的性质，2D正态分布可以是点状（如果方差相似）或线形（如果一个比另一个大得多），或者介于两者之间的任何东西。
点状分布如下图类似，

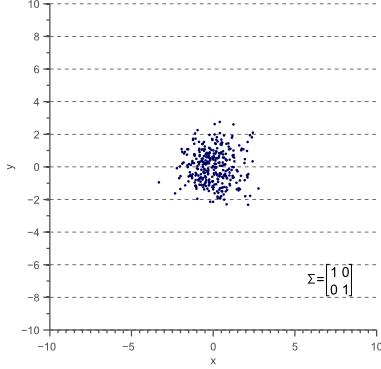
线状分布如下图类似，

在3D情况下，如下图所示，正态分布可以描述一个点或球体（如果方差的幅度在所有方向上相似），一条线（如果一个方向上的方差远大于另外两个方向） 或平面（如果一个方向的方差远小于另外两个方向）。

不同形状的3D正态分布，取决于$\mathbf{\Sigma}$的特征值之间的关系。箭头方向是分布的特征向量方向，长度由特征向量对应的特征值决定。

总结： 通过上面的内容解释了

• 如何使用PDF刻画一个cell内点的分布情况
• 点的分布在不同维度（一维二维三维）下，协方差矩阵的物理含义

6.2 NDT scan registration

6.2.1 优化目标函数构建

使用NDT进行扫描配准时，目标是找到当前帧的pose，使得可以最大化当前帧位于参考帧上的可能性，也就是说需要估计一个当前帧相对参考帧的$R,t$，这里使用$\vec{p}$来表示这个变换。
current scan point cloud 表示如下，
$\mathcal{X}=\left\{\vec{x}_{1}, \ldots, \vec{x}_{n}\right\}$
假设有一个空间变换函数，$T(\vec{p}, \vec{x})$将空间中的点$\vec x$通过$\vec p$变换到另外一个位置。

给定扫描点的一些PDF,$p(\vec x)$（多变量的正态分布表示），最佳变换$\vec p$应该是最大化下面似然函数时候的$\vec p$
$\Psi=\prod_{k=1}^{n} p\left(T\left(\vec{p}, \vec{x}_{k}\right)\right)$
等价于最小化下面的式子,
$-\log \Psi=-\sum_{k=1}^{n} \log \left(p\left(T\left(\vec{p}, \vec{x}_{k}\right)\right)\right)$

这里解释一下为什么是最大化这个似然函数？

• $T(\vec{p}, \vec{x})$是经过source pointcloud,记为$p_{source}$经$\vec p$变换到target pointcloud后的点，记为$p_{target}$
• $p(x)$表示的是描述$p_{target}$中一个点在所在cell中的PDF
• 那么$p(T(\vec{p}, \vec{x}_{k}))$则表示$p_{source}$经过经$\vec p$变换到$p_{target}$坐标系下后在target pointcloud分布下的PDF
• 我们的变换$\vec p$越接近真实值，那么$p(T(\vec{p}, \vec{x}_{k}))$就越贴近$p_{target}$中点的分布，如果所有的点都一一对应上了，相当于所有点的变换这件事情同时发生，所以用连乘机的形式表示，这其实就是最大似然函数的直观意义

举一个二维的例子如下图，

6.2.2 对目标函数进行数学形式的简化

PDF不一定限于正态分布。 任何可以在局部捕获表面点结构并且对异常值稳健的PDF都是合适的。 正态分布的负对数似然增长在远离均值的点处无界。 因此，扫描数据中的异常值可能对结果产生很大影响。 在这项工作中（如Biber，Fleck和Straßer8的论文），使用了正态分布和均匀分布的混合，我称之为混合分布。

$\overline{p}(\vec{x})=c_{1} \exp \left(-\frac{(\vec{x}-\vec{\mu})^{\mathrm{T}} \mathbf{\Sigma}^{-1}(\vec{x}-\vec{\mu})}{2}\right)+c_{2} p_{o}$

• $p_0$ 是异常值的预期比率。 使用此函数，可以限制异常值的影响，如下图所示。
• 常数c1和c2可以通过求$\overline p(\vec x)$的概率质量得到，它equals one
  within the space spanned by a cell。

（什么鬼？）详细的解释参考论文【A Probabilistic Framework for Robust andAccurate Matching of Point Clouds】总之在数学上可以用来近似处理。

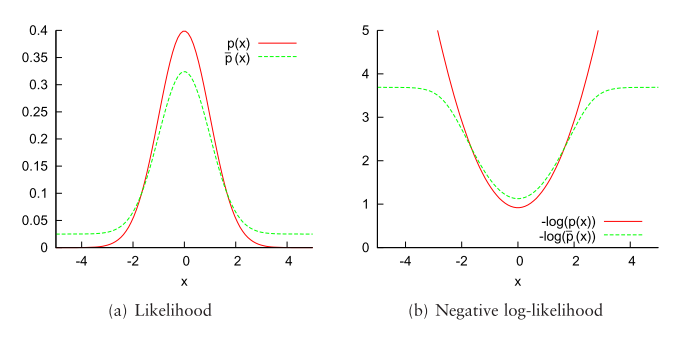
上图是比较正态分布$p(\vec x)$和混合模型$\overline p(\vec x)$。
负对数似然是进行NDT registration时的目标函数，其导数表征了一次特定测量的偏差。（不太理解）
$p(x)$对于非常大的$x$的，the influence grows without bounds,但是$\overline p(\vec x)$却是有界限的。

回顾一下我们的目标函数，

$-\log \Psi=-\sum_{k=1}^{n} \log \left(p\left(T\left(\vec{p}, \vec{x}_{k}\right)\right)\right)$

我们要处理的目标函数中的每一个子项$-\log(p(T(\vec p, \vec x_k)))$具有下列式子的形式（使用前面说的混合模型$\overline p$来描述分布），

$-\log \left(c_{1} \exp \left(-\left((\vec{x}-\vec{\mu})^{\mathrm{T}} \mathbf{\Sigma}^{-1}(\vec{x}-\vec{\mu})\right) / 2\right)+c_{2}\right)$

遗憾是的这个形式没有simplest的一阶导数和二阶导数，像上面的图中展示的那样，我们可以用一个高斯函数来近似负对数函数，也就是可以用

$\tilde{p}(x)=d_{1} \exp \left(-d_{2} x^{2} /\left(2 \sigma^{2}\right)\right)+d_{3}$

来近似

$\overline{p}(x)=-\log \left(c_{1} \exp \left(-x^{2} /\left(2 \sigma^{2}\right)\right)+c_{2}\right)$，

通过拟合参数$d_1,d_2,d_3$使得$\tilde{p}(x)$近似$\overline{p}(x)$,for $x=0, x=\sigma, x=\infty$, 解方程求得
$\begin{aligned} d_{3} &=-\log \left(c_{2}\right) \\ d_{1} &=-\log \left(c_{1}+c_{2}\right)-d_{3} \\ d_{2} &=-2 \log \left(\left(-\log \left(c_{1} \exp (-1 / 2)+c_{2}\right)-d_{3}\right) / d_{1}\right) \end{aligned}$

使用这种高斯近似，则当前扫描中的一个点对NDT的影响可以使用下面的评分函数描述,
$\tilde{p}\left(\vec{x}_{k}\right)=-d_{1} \exp \left(-\frac{d_{2}}{2}\left(\vec{x}_{k}-\vec{\mu}_{k}\right)^{\mathrm{T}} \Sigma_{k}^{-1}\left(\vec{x}_{k}-\vec{\mu}_{k}\right)\right)$（由于$d_3$是一个常量，所以在进行优化的目标函数中可以舍去）

这种形式具有simplest的一阶导数和二阶导数，但在优化中使用时仍具有相同的一般属性。
优化的目标函数变成下面的形式
$s(\vec{p})=-\sum_{k=1}^{n} \tilde{p}\left(T\left(\vec{p}, \vec{x}_{k}\right)\right)$

6.2.3 协方差矩阵的逆$\mathbf{\Sigma}^{-1}$求解

似然函数hu需要协方差矩阵的逆，$\mathbf{\Sigma}^{-1}$。如果cell中的点完全共面或共线，则协方差矩阵是奇异的就无法求逆转。 在3D情况下，从三点或更少点计算的协方差矩阵将始终是奇异的。因此，仅为包含五个以上点的cell计算PDF。 此外，作为对数值问题的预防措施，只要发现$\mathbf{\Sigma}$ is slightly inflated whenever it is found to be nearly singular。 如果$\mathbf{\Sigma}$的最大特征值$\lambda_3$大于$\lambda_1$或$\lambda_2$的100倍，则较小的特征值$\lambda_j$被替换为$\lambda_j=\lambda_3/ 100$。
$\Lambda^{\prime}=\left[ \begin{array}{ccc}{\lambda_{1}^{\prime}} & {0} & {0} \\ {0} & {\lambda_{2}^{\prime}} & {0} \\ {0} & {0} & {\lambda_{3}}\end{array}\right]$

使用$\boldsymbol{\Sigma}^{\prime}=\mathbf{V} \boldsymbol{\Lambda}^{\prime} \mathbf{V}$来代替$\mathbf{\Sigma}$，$\mathbf{V}$中包含的是$\mathbf{\Sigma}$的特征向量。

6.2.4 对目标函数进行优化求解

回顾一下目标函数为，
$s(\vec{p})=-\sum_{k=1}^{n} \tilde{p}\left(T\left(\vec{p}, \vec{x}_{k}\right)\right)$
其中，
$\tilde{p}\left(\vec{x}_{k}\right)=-d_{1} \exp \left(-\frac{d_{2}}{2}\left(\vec{x}_{k}-\vec{\mu}_{k}\right)^{\mathrm{T}} \Sigma_{k}^{-1}\left(\vec{x}_{k}-\vec{\mu}_{k}\right)\right)$

使用Newton法进行求解优化$s(\vec{p})$，核心是求解下面的式子$\mathbf{H} \Delta \vec{p}=-\vec{g}$,其中，

• $H$是$s(\vec{p})$的hessian matrix
• $\vec{g}$是$s(\vec{p})$的gradient vector，或者叫做$s(\vec{p})$的雅克比矩阵的转置$J^T$

定义$\vec{x}_{k}^{\prime} \equiv T\left(\vec{p}, \vec{x}_{k}\right)-\vec{\mu}_{k}$，换句话说，$\vec{x}_{k}^{\prime}$是点$\vec{x}_{k}$变换到reference cell后与reference cell的center的差值。
将目标函数写成，
$s(\vec{p})=\sum_{k=1}^{n} d_{1} \exp (-\frac{d_{2}}{2}(\vec{x}_{k}^{\prime})^{\mathrm{T}} \Sigma_{k}^{-1}\vec{x}_{k}^{\prime})$

The entries $g_i$ of the gradient vector $\vec g$ can be written,
$g_{i}=\frac{\delta s}{\delta p_{i}}=\sum_{k=1}^{n} d_{1} d_{2} \vec{x}_{k}^{\prime \mathrm{T}} \boldsymbol{\Sigma}_{k}^{-1} \frac{\delta \vec{x}_{k}^{\prime}}{\delta p_{i}} \exp \left(\frac{-d_{2}}{2} \vec{x}_{k}^{\prime \mathrm{T}} \mathbf{\Sigma}_{k}^{-1} \vec{x}_{k}^{\prime}\right)$

其中$p_i$是$p$的第$i$的量，比如有三维（6个）和二维（3个）两种情况。

The entries $H_{ij}$ of the Hessian matrix $H$ are

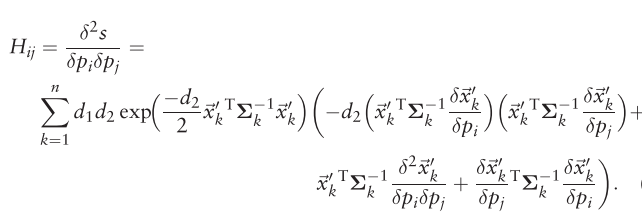
6.2.5 算法流程如下

6.2.5.1 2D NDT公式细节

优化变量为， $\vec{p}=\left[t_{x}, t_{y}, \phi\right]^{\top}$

$T_{2}(\vec{p}, \vec{x})=\left[ \begin{array}{cc}{\cos \phi} & {-\sin \phi} \\ {\sin \phi} & {\cos \phi}\end{array}\right] \vec{x}+\left[ \begin{array}{c}{t_{x}} \\ {t_{y}}\end{array}\right]$

$\delta \vec{x}^{\prime} / \delta p_{i}=\mathrm{J}_{2}=\left[ \begin{array}{ccc}{1} & {0} & {-x_{1} \sin \phi-x_{2} \cos \phi} \\ {0} & {1} & {x_{1} \cos \phi-x_{2} \sin \phi}\end{array}\right]$

$\frac{\delta^{2} \vec{x}^{\prime}}{\delta p_{i} \delta p_{j}}=\left\{\begin{array}{ll}{\left[ \begin{array}{cc}{-x_{1} \cos \phi+x_{2} \sin \phi} \\ {-x_{1} \sin \phi-x_{2} \cos \phi}\end{array}\right]} & {\text { if } i=j=3} \\ {\left[ \begin{array}{c}{0} \\ {0}\end{array}\right]} & {\text { otherwise }}\end{array}\right.$

6.2.5.2 3D NDT公式细节

优化变量为，$\vec{p}_{6}=\left[t_{x}, t_{y}, t_{z}, \phi_{x}, \phi_{y}, \phi_{z}\right]^{\mathrm{T}}$

$T_{E}\left(\vec{p}_{6}, \vec{x}\right)=\mathbf{R}_{x} \mathbf{R}_{y} \mathbf{R}_{z} \vec{x}+\vec{t}=\left[ \begin{array}{ccc}{c_{y} c_{z}} & {-c_{y} s_{z}} & {s_{y}} \\ {c_{x} s_{z}+s_{x} s_{y} c_{z}} & {c_{x} c_{z}-s_{x} s_{y} s_{z}} & {-s_{x} c_{y}} \\ {s_{x} s_{z}-c_{x} s_{y} c_{z}} & {c_{x} s_{y} s_{z}+s_{x} c_{z}} & {c_{x} c_{y}}\end{array}\right] \vec{x}+\left[ \begin{array}{c}{t_{x}} \\ {t_{y}} \\ {t_{z}}\end{array}\right]$

中间量一阶导数，
$\left(\delta / \delta p_{i}\right) T_{E}\left(\vec{p}_{6}, \vec{x}\right)= \mathrm{J}_{E}=\left[ \begin{array}{llllll}{1} & {0} & {0} & {0} & {c} & {f} \\ {0} & {1} & {0} & {a} & {d} & {g} \\ {0} & {0} & {1} & {b} & {e} & {h}\end{array}\right]$

其中，
$\begin{aligned} a &=x_{1}\left(-s_{x} s_{z}+c_{x} s_{y} c_{z}\right)+x_{2}\left(-s_{x} c_{z}-c_{x} s_{y} s_{z}\right)+x_{3}\left(-c_{x} c_{y}\right) \\ b &=x_{1}\left(c_{x} s_{z}+s_{x} s_{y} c_{z}\right)+x_{2}\left(-s_{x} s_{y} s_{z}+c_{x} c_{z}\right)+x_{3}\left(-s_{x} c_{y}\right) \\ c &=x_{1}\left(-s_{y} c_{z}\right)+x_{2}\left(s_{y} s_{z}\right)+x_{3}\left(c_{y}\right) \end{aligned}$
$\begin{aligned} d &=x_{1}\left(s_{x} c_{y} c_{z}\right)+x_{2}\left(-s_{x} c_{y} s_{z}\right)+x_{3}\left(s_{x} s_{y}\right) \\ e &=x_{1}\left(-c_{x} c_{y} c_{z}\right)+x_{2}\left(c_{x} c_{y} s_{z}\right)+x_{3}\left(-c_{x} s_{y}\right) \\ f &=x_{1}\left(-c_{y} s_{z}\right)+x_{2}\left(-c_{y} c_{z}\right) \\ g &=x_{1}\left(c_{x} c_{z}-s_{x} s_{y} s_{z}\right)+x_{2}\left(-c_{x} s_{z}-s_{x} s_{y} c_{z}\right) \\ h &=x_{1}\left(s_{x} c_{z}+c_{x} s_{y} s_{z}\right)+x_{2}\left(c_{x} s_{y} c_{z}-s_{x} s_{z}\right) \end{aligned}$

中间量二阶导数，
$\left(\delta^{2} /\left(\delta p_{i} \delta p_{j}\right)\right) T_{E}\left(\vec{p}_{6}, \vec{x}\right)=\mathrm{H}_{E}=\left[ \begin{array}{ccc}{\vec{H}_{11}} & {\cdots} & {\vec{H}_{16}} \\ {\vdots} & {\ddots} & {\vdots} \\ {\vec{H}_{61}} & {\cdots} & {\vec{H}_{66}}\end{array}\right]=\left[ \begin{array}{cccccc}{\overrightarrow{0}} & {\overrightarrow{0}} & {\overrightarrow{0}} & {\overrightarrow{0}} & {\overrightarrow{0}} & {\overrightarrow{0}} \\ {\overrightarrow{0}} & {\overrightarrow{0}} & {\overrightarrow{0}} & {\overrightarrow{0}} & {\overrightarrow{0}} & {\overrightarrow{0}} \\ {\overrightarrow{0}} & {\overrightarrow{0}} & {\overrightarrow{0}} & {\vec{a}} & {\overrightarrow{0}} & {\overrightarrow{0}} \\ {\overrightarrow{0}} & {\overrightarrow{0}} & {\overrightarrow{0}} & {\vec{b}} & {\vec{b}} & {\vec{c}} \\ {\overrightarrow{0}} & {\overrightarrow{0}} & {\overrightarrow{0}} & {\vec{c}} & {\vec{e}} & {\vec{f}}\end{array}\right]$
其中，
$\vec{a}=\left[ \begin{array}{c}{x_{1}\left(-c_{x} s_{z}-s_{x} s_{y} c_{z}\right)+x_{2}\left(-c_{x} c_{z}+s_{x} s_{y} s_{z}\right)+x_{3}\left(s_{x} c_{y}\right)} \\ {x_{1}\left(-s_{x} s_{z}+c_{x} s_{y} c_{z}\right)+x_{2}\left(-c_{x} s_{y} s_{z}-s_{x} c_{z}\right)+x_{3}\left(-c_{x} c_{y}\right)}\end{array}\right]$
$\vec{b}=\left[ \begin{array}{c}{0} \\ {x_{1}\left(c_{x} c_{y} c_{z}\right)+x_{2}\left(-c_{x} c_{y} s_{z}\right)+x_{3}\left(c_{x} s_{y}\right)} \\ {x_{1}\left(s_{x} c_{y} c_{z}\right)+x_{2}\left(-s_{x} c_{y} s_{z}\right)+x_{3}\left(s_{x} s_{y}\right)}\end{array}\right]$
$\vec{c}=\left[ \begin{array}{c}{x_{1}\left(-s_{x} c_{z}-c_{x} s_{y} s_{z}\right)+x_{2}\left(-s_{x} s_{z}-c_{x} s_{y} c_{z}\right)} \\ {x_{1}\left(c_{x} c_{z}-s_{x} s_{y} s_{z}\right)+x_{2}\left(-s_{x} s_{y} c_{z}-c_{x} s_{z}\right)}\end{array}\right]$
$\vec{d}=\left[ \begin{array}{c}{x_{1}\left(-c_{y} c_{z}\right)+x_{2}\left(c_{y} s_{z}\right)+x_{3}\left(-s_{y}\right)} \\ {x_{1}\left(-s_{x} s_{y} c_{z}\right)+x_{2}\left(s_{x} s_{y} s_{z}\right)+x_{3}\left(s_{x} c_{y}\right)} \\ {x_{1}\left(c_{x} s_{y} c_{z}\right)+x_{2}\left(-c_{x} s_{y} s_{z}\right)+x_{3}\left(-c_{x} c_{y}\right)}\end{array}\right]$
$\vec{e}=\left[ \begin{array}{c}{x_{1}\left(s_{y} s_{z}\right)+x_{2}\left(s_{y} c_{z}\right)} \\ {x_{1}\left(-s_{x} c_{y} s_{z}\right)+x_{2}\left(-s_{x} c_{y} c_{z}\right)} \\ {x_{1}\left(c_{x} c_{y} s_{z}\right)+x_{2}\left(c_{x} c_{y} c_{z}\right)}\end{array}\right]$
$\vec{f}=\left[ \begin{array}{c}{x_{1}\left(-c_{y} c_{z}\right)+x_{2}\left(c_{y} s_{z}\right)} \\ {x_{1}\left(-c_{x} s_{z}-s_{x} s_{y} c_{z}\right)+x_{2}\left(-c_{x} c_{z}+s_{x} s_{y} s_{z}\right)} \\ {x_{1}\left(-s_{x} s_{z}+c_{x} s_{y} c_{z}\right)+x_{2}\left(-c_{x} s_{y} s_{z}-s_{x} c_{z}\right)}\end{array}\right]$

6.3 3D-NDT extensions

• 3D-NDT最重要的参数是 cell size
  
  • size too large, less precise registration
  • cell的影响区域只延伸到其边界，如果cells太小, registration will only succeed if the two scans are initially close together
  • 另一个问题是，对于较小的cell，可能根本不使用具有低点密度的部分扫描，因为计算可信的协方差矩阵至少需要5个点
  • Using smaller cells also requires more memory

因此，cell的最佳尺寸和分布取决于输入数据的形状和密度，还取决于我们对scan表示的保真度的要求。

使用方形或立方体cell的固定格子需要用户选择良好的cell尺寸。

更灵活的cell结构将是优选的：在可能的情况下使用大cell并且在单个正态分布不能令人满意地描述表面的地方进行更精细的细分。 本节介绍了许多用于创建NDT cell结构和相关似然函数的替代方法

6.3.1 Fixed discretisation

不考虑刚才提到的缺点，使用固定单元格的好处是初始化和使用单元结构的开销非常小。 每个单元只需要计算一组参数，每个单元的定位都很简单。 对于算法的性能而言，更重要的是点对单元查找可以在恒定时间内非常快速地完成，因为单元可以存储在简单的阵列中。

6.3.2 Octree discretisation

八叉树是一种常用的树形结构，可用于存储三维空间的hierarchical discretisation。在八叉树中，每个节点表示空间的有界分区。每个内部节点有八个子节点，表示其父节点的空间分区的全等和非重叠细分。创建八叉树时，根节点的大小适合包含整个参考扫描。然后递归地构建树，分割包含多于一定数量点的所有节点。所有数据点都包含在八叉树的叶节点中。八叉树与kD树非常相似，但每个内部节点有八个而不是两个子节点。

如前所述，八叉树版本的3D-NDT以fixed regular cells开始，不同之处在于每个单元格是八叉树的根节点。分布的方差大于特定阈值的单元被递归地分割，形成八叉树林。

对于NDT的效率而言，点到cell查找速度快是很重要的，这是使用forest of octrees的主要原因，而不是具有跨越所有扫描的根节点的单个八叉树。对于许多类型的扫描数据，可以指定合理的基本单元尺寸，从而仅需要分割扫描表面特别不均匀的部分中的少数单元。因此，对于大多数点，找到正确的单元只需要单个数组访问，而每个点遍历一个八叉树需要更多的时间。森林需要比单个树更多的内存，特别是如果每棵树的根节点的单元格大小很小，但是对于本文提出的实验，这种影响可以忽略不计

6.3.3 Iterative discretisation

另一种选择是使用每次运行的最终pose作为下一次运行的初始pose，以连续更精细的cell分辨率执行多次NDT运行。 第一次运行有利于将对齐的scan更紧密地结合在一起，后面的运行可以改善粗略的初始匹配。

6.3.4 Adaptive clustering

更自适应的离散化方法是使用聚类算法，该算法基于扫描点的位置将扫描点划分为多个聚类，并且为每个聚类使用一个NDT单元。一种易于实现的常见聚类算法是k-means聚类29，

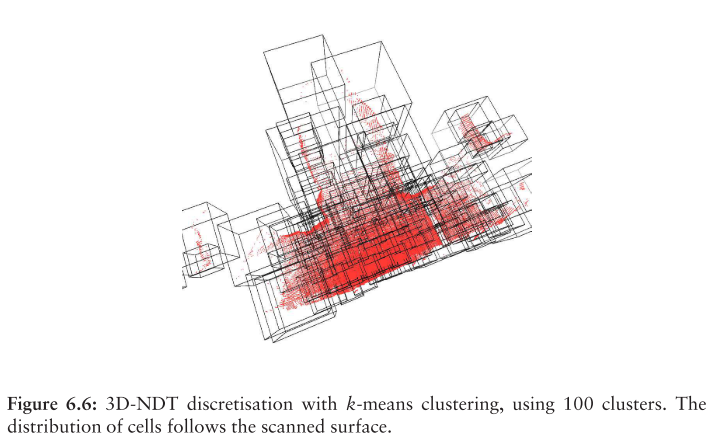
6.3.6 Trilinear interpolation

$\hat{p}(\vec{x})=\sum_{b=1}^{8}-d_{1(b)} w\left(\vec{x}, \vec{\mu}_{b}\right) \exp \left(-\frac{d_{2(b)}}{2}\left(\vec{x}-\vec{\mu}_{b}\right)^{\mathrm{T}} \Sigma_{b}^{-1}\left(\vec{x}-\vec{\mu}_{b}\right)\right)$

将NDT应用于矿井隧道扫描的图示，具有（右）和不带（左）三线性插值。 密度较大的区域代表较大的分数值。 (暗网格图案不代表较小的分数值，但仅显示底层单元格的边界)

• trilinear interpolation耗时4倍
• cell间更平滑

6.4 Experimental evaluation

6.4.1 Influence of NDT parameters

• Straight
  straight mine-tunnel section without many prominent features. 两次扫描之间的距离在参考姿势处为5m，角度为4.7°。 扫描包含约95 000点
• Crossing
  没有移动，两次扫描之间的重叠量约为100％，rt应该接近于零
• Sci-Fi(仿真数据)
  仿真数据，扫描之间的平移偏移为5米，没有旋转偏移。 换句话说，两次扫描之间的重叠量约为80％。 扫描每个包含大约46,000个点。
• Sim-Mine(模拟矿井隧道)
  模拟矿井隧道， 与Straight数据集类似，此扫描对构成了相当大的挑战。 在这种情况下，模拟激光扫描仪的最大范围为20米，两个位置之间的平移差为5米，因此两次扫描之间的重叠率为75％。 同样，视野水平180°，垂直145°。 每次扫描包含大约75 000个点。
• 3D-Cam
  3D-Cam数据集由Jacobs University Bremen的机器人小组用SwissRanger相机收集，两次扫描之间的重叠量约为65％，每个包含约25000个点。

两个模拟激光雷达扫描实验对都使用yaw扫描仪，其中与垂直轴重合的2D扫描平面围绕垂直轴扫描以产生3D扫描。 真实的3D扫描使用配置用于俯仰扫描的激光雷达，其中水平扫描平面向上和向下倾斜以产生3D扫描。

在以下实验中，添加到初始姿态估计的基线偏移是4个平移扫描对的1m平移和0.2rad旋转。 在迭代离散化方案中使用的cell尺寸是2m，1m和0.5m。 3D-Cam扫描比其他扫描具有更小的比例，并且重叠更少。
因此，对于该扫描对，初始平移误差的幅度较小，0.5m而不是1m，并且初始旋转误差是0.1rad。 此外，使用较小的NDT单元尺寸：0.5m，0.25m和0.125m。

• Ground truth
  real word做几组实验，人工挑选出匹配的比较好的，或者求几组实验的平均值认为是好的值。
  simulated word是有真值的

6.4.1.1 Cell size

• 太大，则单个高斯不能很好地描述每个cell内的结构
• 太小，则高斯分布可能受扫描仪噪声的支配
• 对于稀疏采样点云，如果cell很小，则每个cell内可能存在太少的点来计算可靠的密度函数
• 最佳cell大小最依赖于输入数据的规模

选取cell size的总结：

• 最佳cell大小最依赖于输入数据的规模，也取决于扫描表面的结构数量（特征丰富程度）
  对于移动机器人上面的应用来讲，cell size取1m到2m
• 对于表面结构简单，比如矿井，对于cell size就比较敏感，取小点比较好
• cell size对于平移error影响比较大，对于rotaion error影响比较小
• cell较大（因此较少）时，运行时间通常略短，但差异相当小。cell小的时候时间多是因为，一些附加的时间花在了初始化单元格上面了。事实上每次进行迭代的优化时间不受cell size影响。

6.4.1.2 Discretisation methods

固定的单元网格可能不是最佳的，并且如上所述，找到满足捕获下面的表面结构的一个单元尺寸并不总是容易的。 因此，建议使用6.3节中描述的更灵活的离散化方法之一。

• fixed cell

  fixed cell设置的性能相当差，从图6.12中标记为F的每个数据集的最左侧框图可以看出。

• octree discretisation

  通过octree discretisation，分裂具有大变化的cell，cell结构比使用fixed cell时更好地遵循表面形状。但这是否会导致更好的注册结果取决于扫描数据。

  对于此处研究的大多数扫描对，octree discretisation并未导致对fixed cell 的显着改善（比较标记为F和O的图）。Straight data set是例外，与固定单元相比，使用八叉树时成功率从54％增加到87％。

  其他数据集缺乏改进的可能原因是不需要更详细的表面表示，因为它们具有足够突出的特征并且即使不考虑更精细的细节也可以进行registered。即使是困难的Sim-Mine数据也没有从octree discretisation中获益。虽然一些小规模的结构以不均匀的墙壁的形式存在，但是墙壁比真实的矿井数据更平滑，更详细的octree discretisation对这里评估的cell size没有帮助。

• iterative discretisation

  与octree discretisation提升的相当有限的值相比，图6.12显示iterative discretisation大大提高了3D-NDT的稳健性。比较标记为I到F和O的图。

  对于Straight数据集，使用iterative discretisation（没有linked cells or interpolation）的成功注册次数几乎是固定2m单元格的两倍，比使用具有相同尺寸的octree discretisation时大12％。

  对于Sim-Mine数据集，与fixed cell相比，成功率几乎高出三倍。使用3D-Cam和Crossing数据可以看到相同的趋势，尽管这些扫描对的差异并不大。

  在所有情况下，使用iterative discretisation时3D-NDT的中值误差非常小，并且异常值（具有非常差的最终姿势估计的登记尝试）也更小。

  关于iterative discretisation方案的一个重要注意事项是，即使在使用iterative discretisation时每次注册尝试3D-NDT运行三次，运行时间也不是使用fix cell时的三倍。平均执行时间大约是使用fix cell 的单次运行时的两倍。这种效应的原因是该算法通常只使用更精细的单元网格执行几次牛顿迭代，因为在最粗糙级别进行注册后的姿态估计已经非常接近最终解决方案。运行时间的差异可能会更低。

在每个NDT迭代中创建一个全新的NDT网格的意义上，当前的实现并不是最优的。更有效的实现将首先计算高分辨率单元，并使用它们来快速计算较低分辨率单元的分布函数。

• Kmeans
  

  还评估了k均值聚类方法，但结果未包括在图6.12中。由于cell结构没有规律性，正如其他离散化方法一样，将cell存储在静态阵列中并不适合这种离散化。相反，cells或者更确切地说是clusters存储在kD树中。使用树搜索结构与启用linked cells具有相同的效果，因为在搜索kD树时总是找到最近的集群。此方法比标准3D-NDT花费更多时间，主要是因为聚类步骤所需的时间。与使用fixed cell时一样，clusters大小有一个最佳范围。使用太少的clusters（这意味着它们太大）或太多的clusters（因此太小）会使结果变得更糟。对于3D-Cam数据集，最好约50个clusters，导致平均clusters大小为0.7m。对于300到500个clusters之间的其他数据集是最好的，导致平均大小约1-2米。虽然这种自适应聚类比fixed cell或octotree设置更好，但使用iterative discretisation通常在更短的时间内产生至少同样好的结果。有关不同clusters数的结果图，请参阅附录C.6

6.4.1.3 Linked cells

6.4.1.4 Trilinear interpolation

6.4.1.5 Sample ratio

6.4.1.6 Sampling method

6.4.1.7 Conclusions regarding NDT parameters

• 基于图6.12所示的结果，似乎很清楚，使用3D-NDT的最佳方法是对linked cell进行迭代离散化,几乎没有理由使用八叉树离散化方法。
• 另一方面，迭代离散与基本方案相比，在合理的执行时成本下有了很大的改进。
• 如果快速执行速度不重要，带有三线性插值的3D-NDT可提供最稳健的配准结果，尽管执行时间通常比非插值NDT长约四倍。
• 即使采用灵活的离散化技术，cell的整体规模也必须根据传感器选择，尽管对选择不良的size的容忍度仍然大于使用fixed cell的容忍度。
• 对于具有a large field of view和20-40m范围的三维SICK-激光雷达扫描，2m和0.5m之间的单元尺寸通常非常好。对于具有小得多的视场和大约7米范围的飞行时间相机的数据，0.5m和0.1m之间的单元尺寸更合适。

6.4.2 Registration robustness

扫描配准算法的最重要特征可能是其对初始pose估计中的误差量的鲁棒性。 即使面对远离solution的初始pose估计，良好的注册算法也应收敛到紧密对齐。 本节介绍为评估初始pose的平移和旋转分量中的误差的配准鲁棒性而执行的实验。

6.4.2.1 Robustness of 3D-NDT to initial error in comparison with ICP Robustness

分开评估关于初始平移和旋转估计的鲁棒性。 对于平移误差测试，初始旋转误差设置为零。 反之亦然，在测试初始旋转误差的灵敏度时，平移误差为零。 具有基线参数设置的3D-NDT旋转误差测试结果如图6.14所示，平移误差测试如图6.16所示。最终旋转误差未在图6.16中显示，因为它遵循与最终平移误差相同的趋势。有关完整图片，请参阅附录C.3。

6.4.2.2 General NDT performance

使用baseline 设置，并使用在这些测试中分布在所有方向上的误差偏移，NDT处理初始姿态估计中的误差，最多0.5米平移或0.2弧度旋转，激光雷达扫描没有失败，即使对于困难的Straight和Sim-Mine数据集也是如此 。 只需很少的失败register尝试就可以处理高达2米平移或0.5弧度旋转的姿势误差，并且对于成功的尝试，pose中值误差仍然非常小。 使用三线性插值时，鲁棒性仍然更大（如附录C.3和C.4所示）。 所有具有高达0.5 rad初始误差的尝试都成功进行激光雷达扫描。 3D-Cam扫描对的情况不同，因为2m平移误差通常意味着两次扫描之间没有重叠。 对于这一对，已经发生了一些failure，具有0.25m的误差偏移，并且两次扫描实际上不可能在大于1m的初始偏移处进行register。

6.4.2.3 ICP comparison

将NDT与ICP进行比较，可以看出：

• 中值误差通常是使用NDT后比使用ICP后略小
• 与比较图6.14和6.15相比，NDT对于大转数偏移也比ICP更加稳健
• 对于rotation误差，ICP的性能也会降低，而NDT可以很好地处理高达0.5 rad的旋转误差（除了3D-Cam扫描对）
• 对于translation误差，二者性能相差不大，但是NDT表现还是更好
• ICP的执行时间对offset（包括旋转和平移）变大而迅速变大；而NDT变化不大

6.4.2.4 Collaborative performance comparison

在评估新方法时，可能会对“我的宝宝”综合症感到敏感。 在进行比较研究时，注意对新方法的任何偏见是很重要的。 对于迄今为止所呈现的结果，以及我们小组[64-66]中关于扫描注册的先前出版物，我自己的ICP实施用于比较ICP和NDT的性能。 尽管我们（当然）试图公平客观，但有些读者可能怀疑之前提出的结果的有效性。例如，可能是ICP的不良性能仅仅是参数选择不良的结果。 ICP与NDT一样，有几个参数可供选择，多年来已发布ICP的众多变体和补充内容。

还有其他团队与ICP进行了更广泛的合作，并且具有更多实际操作经验，了解它如何使用不同的参数值和不同类型的数据。 作为对先前结果的检查，与奥斯纳布吕克大学的AndreasNüchter，ChristopherLörken和Joachim Hertzberg一起进行了合作比较。我们将NDT与他们在矿山测绘场景中的ICP实施进行了比较。Osnabrück集团广泛使用ICP进行室内和室外移动机器人绘图，并且还对基本算法进行了一些改进[10,77-81]。 这项工作先前已在IEEE国际机器人与自动化会议上发表[69]。

6.4.2.5 Experimental setup

用于该实验的数据集包括来自略微弯曲的隧道部分的两次扫描。 它们与Straight和Sim-Mine数据集的特征非常相似。 两次扫描都是subsampled。 用于register的采样扫描每个包含8000个点（约占总点数的10％）。 它们如图6.18所示。

一致reference pose，并且register算法在许多pose下运行，其中不同的平移和旋转偏移被添加到Reference pose，类似于先前的实验。 该实验的设置的一个不同之处在于初始pose估计的偏移限于水平平面中的旋转和平移。
这种约束可以有三个原因：

• 第一，在典型的矿山测绘场景中，误差的最大部分将位于水平面上;
• 其次，它减少了必须运行的试验次数（我们评估了441次start pose，在所有转换参数上使用相同的偏移将制造250047种poses）;
• 第三，它使结果更容易可视化。

register算法没有添加任何约束; 他们仍然以六个自由度运作。
选择两个平移阈值来确定register是否成功：更严格(strict)的一个0.20m，一个更弱(loose)的1.0m。 使用的旋转阈值为5°（0.087 rad）。 对于人类观察者来说，更严格的平移阈值内的pose难以分辨。具有较大平移误差的pose显然不太精确匹配，但是较弱平移阈值内的那些仍然指示了何时register算法能够收敛于“合理”的solution以及何时会失败。

6.4.2.6 Results

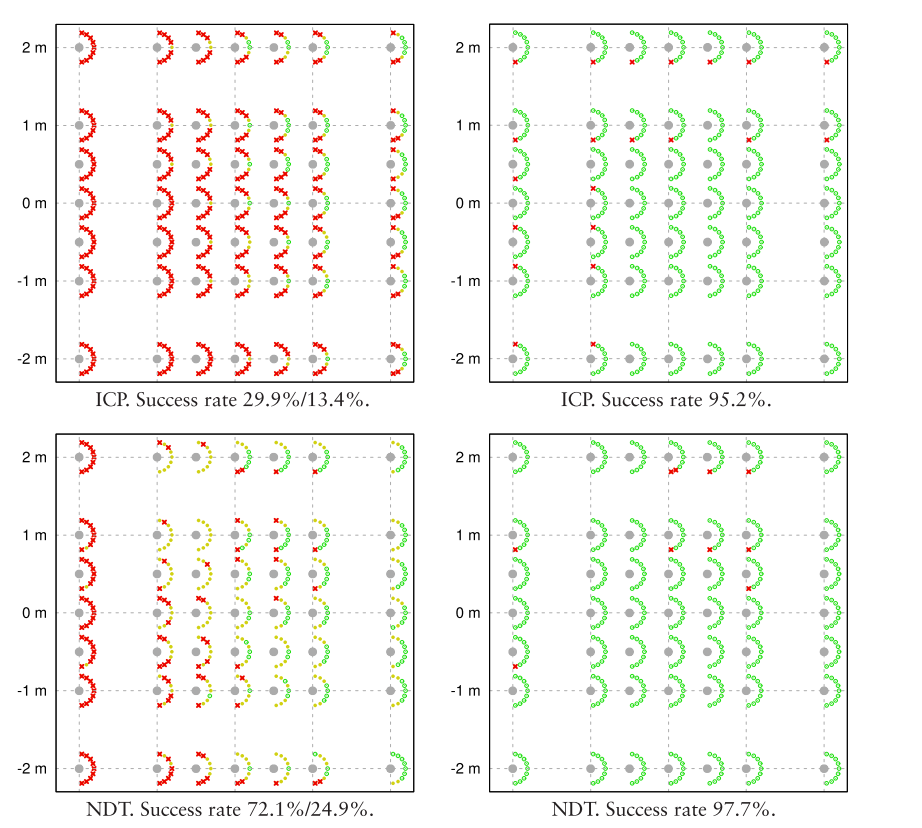
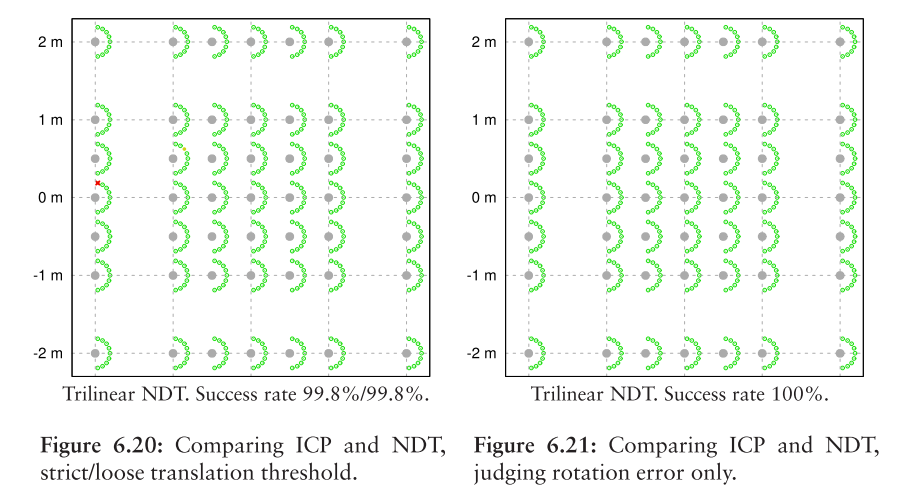
结果以图形方式显示在图6.20和6.21中。在这些图中，初始平移偏移沿x和y轴布置，旋转偏移显示为围绕圆的点。 每组点显示九个起始pose的结果，具有相同的平移但不同的旋转。（有关说明，请参见图6.19。）这种类型的可视化使得可以查看哪些pose对于配准算法来说是困难的。

如图6.20所示，ICP在大多数初始平移具有“向后”偏移（即-x方向偏移中的偏移）的尝试中都失败了。虽然在register后pose估计的旋转通常是（见图6.21），但这些情况下的算法过早地以最大pose停止两次扫描之间重叠。只有13％的register尝试，ICP在reference pose的20厘米范围内，但最终的旋转估计在95％的情况下是正确的。NDT也克服了NDT的局部最优解困难。在更多情况下，尽管对NDT来讲，估计固具有-x平移偏移的pose是困难的，但是通过使用具有三线性插值的NDT可以提高register成功率，但代价是更长的执行时间。

具有插值的NDT在所有情况下都找到了正确的旋转和平移，但是除了其中一项平移试验外，这个实验的失败和其他所有算法的失败的原因一样，因为插值NDT register尝试失败也是由于平移offset太远了，从而两次扫描之间的重叠太小了。

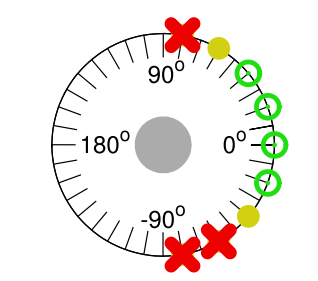
这个图是图6.20-6.21中的细节。 每个子图表示一组具有相同平移偏移和不同旋转偏移的初始pose。 严格(strict)的一个0.20m，松弛(loose)的1.0m

• 绿色圆圈表示使用strict平移阈值的成功注册
• 实心黄色圆点表示使用loose阈值的成功
• 红色十字表示失败
• 对于每个平移偏移，pose的初始旋转误差范围为-80°到+ 80°，20°增量
• 中心灰点标记平移偏移

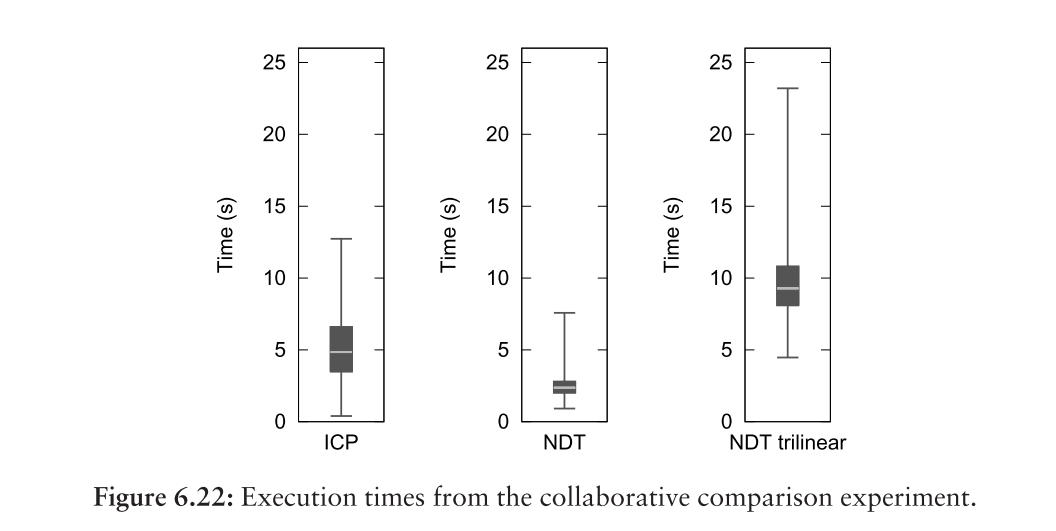
执行时间如图6.22所示。 至于本章中的其他时序结果，报告的时间包括所有必要的预处理（包括创建NDT的正态分布和ICP的kD树）以及NDT的所有三次迭代，但不包括加载扫描数据所需的时间。NDT的执行时间中位数约为ICP执行时间的一半。 具有三线性插值的NDT比没有插值的NDT长大约四倍，如前所述，或者是ICP的两倍。 这些测试是在配备1.6 GHz Intel Celeron CPU和2 GiB RAM的笔记本电脑上运行的。虽然这种比较的结果不能说具有统计学意义，但他们没有理由相信本章介绍的ICP与NDT之间的其他比较具有误导性。

6.4.3 Registration with mobile robots

之前的实验都在受控环境中使用少量单独的扫描对。本节介绍在更大规模的mapping方案中使用两个更大的数据集来评估NDT的结果。这些数据集是通过在Kvarntorp矿井中运行移动机器人获得的，每隔几米停一下进行一次3D扫描。对于本节中介绍的实验，初始psoe估计值来自机器人的odometry。这种设置更像是移动机器人应用程序中可以predict的，而不是之前部分中用于成对实验的直接进行设置，其中使用了一组100个预定义的误差偏移而不是odometry。然而，第6.4.1和6.4.2节中的实验可以被认为是更完整的，因为对于那些实验，算法是从更大的一组可能的起始pose进行测试的，并且更彻底地研究了算法的性质。以下评估中使用的数据集如下所述。

• Kvarntorp-Loop
  使用Tjorven收集该数据集。 机器人沿着两条隧道行驶，3D扫描花四到五分钟。图6.23展示了该数据集的48次扫描，每次扫描的Reference pose如图所示。 扫描包含每个90000点的顺序。
  在Kvarntorp-Loop数据集中，从一次扫描到下一次扫描，初始姿势误差高达1.5m和0.2rad（11°）。 假设每次扫描的大小约为10米乘30米，则0.2弧度的旋转误差很大，导致扫描距离较远的点位移6米。 图6.24显示了不良测距的一个例子，它显示了来自Kvarntorp-Loop的扫描48和49，扫描49的pose估计来自odometry。
  
  

• Mission-4
  使用Kurt3D机器人（第4.3节）在Kvarntorp矿井，收集了四个独立的扫描序列（或“mission”）。这里使用了最长的序列，mission4。该数据集包括来自闭环的55次扫描，最后几次扫描与第一次扫描重叠。扫描每个包含约75000个点。从odometry测量转弯角度是有问题的，特别是当在一个松散的岩石表面上驾驶小型滑移车辆时，就像这种情况一样。在Mission-4数据集中，来自odometry的最差pose估计是Scan 33，其初始旋转误差不小于1.4 rad（85°）。Mission-4数据集的其他扫描具有类似于Kvarntorp-Loop的odometry误差幅度。 Mission-4数据集如图6.25所示。最有问题的扫描如图6.26所示
  
  

再次，通过运行多次register尝试来确定Reference pose，并且将视觉上最佳匹配的平均值用作每个扫描对的参考pose。 成功register的限制设置为0.20m和0.05弧度，如第6.4.1节所述。

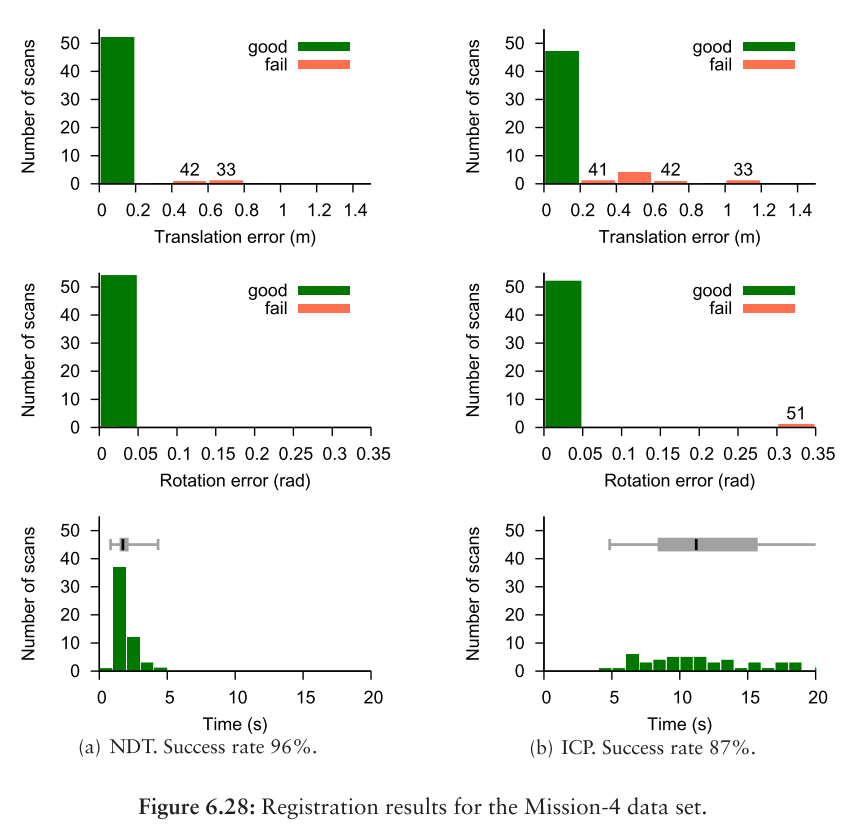
register结果以图6.27和6.28中的运行时间和最终pose误差的直方图表示。在判断配准鲁棒性时，这些图的最重要特征是“平移错误”和“旋转错误”，图中最左侧直方图框的高度显示了成功register的数量。最左侧的框右侧显示失败的register（错误较大的结果位于图中的右侧）。只有一个条目的直方图框标有相应的扫描编号，以便更清楚地记录哪些扫描无法注册。 图中还包括显示结果的执行时间分布的箱形图。

图6.27显示了在Kvarntorp-Loop数据集上使用NDT和ICP的结果。两种算法的性能非常相似，但NDT的执行速度比ICP快得多。 使用NDT的三线性插值，可正确记录此数据集的所有扫描。ICP（0.5m）和低收敛阈值（10-6m）的相对较短的离群值拒绝阈值距离迫使算法采取大量小步骤，这会影响运行时间。然而，在许多情况下，使用更大的阈值会使精度更差，并且第5.1节中提到的减小阈值策略使得算法对初始pose估计中的大误差不太鲁棒。其他ICP参数设置和插值NDT的结果包含在附录C.7中。

Mission-4数据集的结果如图6.28所示。例如，NDT和ICP之间的性能差异较大。在55次扫描中，53次使用迭代NDT正确注册。 所有注册尝试都在旋转误差阈值范围内，但扫描33和42收敛到具有较大重叠的pose。使用ICP注册数据集时，七次扫描的最终平移误差高于阈值，一次扫描的最终旋转错误。 使用基线参数设置，ICP的执行时间要比NDT长得多。 使用NDT的三线性插值，只有一个失败：扫描42

可以得出结论，对于移动机器人配准实验中遇到的初始姿态误差的大小和方向，ICP和NDT之间的鲁棒性差异不如6.4.2节中的综合测试那么大。 尽管如此，评估表明NDT对几乎所有数据集都更加健壮，而且执行速度更快。

6.4.4 Summary of experiments

最值得注意的是，当呈现无特征的隧道扫描和噪声很小的重叠扫描数据时：

• NDT is more robust to large error offsets in the initial pose estimate

• NDT gives more accurate registration results

• NDT without interpolation is also faster than ICP

• Both algorithms require certain threshold values to be chosen according to the scale and shape of the input data
• most important params
  
  • ICP: outlier-rejection distance threshold。使用ICP时，如何处理扫描非重叠部分的异常值并不总是显而易见的
  • NDT最重要参数是cell size。NDT的似然函数为基于局部表面形状的异常值拒绝提供了合理的标准,还必须根据手头的扫描数据设置cell大小，尽管iterative discretisation策略使得算法对不良参数选择不太敏感。

6.5 Other authors’ NDT variants

Duckett和我在2005年首次提出了3D-NDT出版物[64,65]。后来，其他作者也发表了独立于Biber和Straßer工作的registration方法7。

Ripperda和Brenner [88]提出了一个semi-3D version of NDT，并通过注册大型高分辨率室外扫描进行了演示。在他们的工作中，每个3D扫描被分成几个水平切片，并且在每对切片上使用2D-NDT。 使用k个切片，并通过$s_{i}(\vec{p})$表示切片i的pose$\vec p$的得分，Ripperda和Brenner使用的得分函数是所有切片对（slice pairs）的总和：

$$s(\vec{p})=\sum_{i=1}^{k} s_{i}(\vec{p})$$
Ripperda和Brenner的方法只能在一个平面上执行配准，因此只能在假设所有扫描的局部坐标系在平面中对齐的情况下工作，这意味着扫描仪必须在每个扫描pose处保持水平。 这种假设并不适用于大多数移动机器人的应用。

在Takeuchi和Tsubouchi [99]的2006年论文中，NDT独立扩展到3D。它们的实现与第6.3节中描述的3D-NDT版本非常相似，因为它们也使用迭代细分（iterative subdivision）方案。一个重要的区别是Takeuchi和Tsubouchi在传感器位置附近使用较小的单元格，在早期迭代中使用较远的较大单元格，并且在扫描几乎对齐时在后面的迭代中仅使用较小的单元格。基本原理是旋转估计中的误差导致距传感器位置更远的位移，因此需要更大的单元以确保使用来自当前扫描的更多点。第6.3.5节中描述的linked cell策略是针对同一问题的另一种解决方案。Takeuchi和Tsubouchi使用他们的算法报告了来自计算机实验室的数据的良好结果，但据我所知，与其他方法的比较尚不清楚。

Kaminade等人提出了另一项NDT扩展。 在2008年[56]，提出了2D-NDT扫描注册的变体。他们的工作的主要贡献是迭代配准方案，其中NDT cell的协方差矩阵在每次迭代中被不同的量模糊，而不改变单元尺寸。 Kaminade等。使用cell的原始协方差矩阵的相似变换，$\boldsymbol{\Sigma}=\mathbf{V} \boldsymbol{\Lambda} \mathbf{V}^{\mathrm{T}}$，其中$\mathbf{V}$包含$\boldsymbol{\Sigma}$的特征向量和

$$\boldsymbol{\Lambda}=\left[ \begin{array}{cc}{\lambda_{1}} & {0} \\ {0} & {\lambda_{2}}\end{array}\right]$$
Kaminade等人的算法中使用的协方差矩阵是
$$\mathbf{\Sigma}^{\prime}=\mathbf{V} \boldsymbol{\Lambda}^{\prime} \mathbf{V}^{\mathrm{T}}$$
$$\boldsymbol{\Lambda}^{\prime}=\left[ \begin{array}{cc}{K \lambda_{1}} & {0} \\ {0} & {K \lambda_{2}}\end{array}\right]$$
$K$是一个“blurring factor”。将Σ替换为Σ'类似于避免几乎奇异的协方差矩阵所采用的inflation（公式6.11），尽管模糊因子K的值通常比公式6.11中引入的轻微模糊具有更强的效果。 在Kami-nade等人描述的实验中，使用1至100的K值。 Kaminade在标准NDT中不使用array-based point-to-cell方法，为定位到unoccupied cells中的点，而使用kD树搜索找到最近occupied NDT cell。这些添加也与第6.3节中所示的iterative discretisation和linked cell方法非常相似。通过使用从六足移动机器人收集的2D范围数据的实验，Kaminade等人。 与标准2D-NDT相比，使用迭代2D-NDT显示出改进的配准精度。

6.6 Confidence measure

注册两次扫描后，是否可以在不知道基本事实的情况下确定注册质量？注册的输出是一个新的pose估计，但是可以测量该估计的好坏程度吗？定性地确定注册是否成功的一种方法是在输出pose处查看扫描并可视地确定匹配是否良好。然而，非常希望有一个可量化的因子，因为我们想区分局部和全局最优，表示为$Q(\mathcal{X}, \mathcal{Y}, \vec{p})$。一般来说，这当然是一个非常困难的问题，确保pose$\vec p$处的两个扫描X和Y的配准质量，这看起来不可能的。我们唯一希望的是，使用针对该问题的特定领域知识，可以合理地做出成功和失败注册之间的区别。

6.6.1 NDT得分度量

对于质量测量而言，最明显的选择可能是NDT得分功能。毕竟，这是使用NDT进行扫描注册时优化的功能。让我们将此度量定义为

$$Q_{s}(\mathcal{X}, \mathcal{Y}, \vec{p})=\frac{1}{n} s(\vec{p})$$
where，$s(\vec{p})=-\sum_{k=1}^{n} \tilde{p}\left(T\left(\vec{p}, \vec{x}_{k}\right)\right)$
一个好的匹配应该给出一个很大的负$Q_s$值。 使用缩放因子$1 / n$以获得与扫描中的点数无关的分数值

6.6.2 Hessian的逆的特征值度量

另一种评估方法是在最终pose估计时研究NDT评分函数的Hessian。逆Hessian矩阵可以用作pose参数的协方差矩阵的估计[39]，并且因此给出了可以确定每个姿势参数的确定性的指示。考虑到Hessian的逆的特征值，如果所有特征值都很小，则配准可能是好的，这意味着所有参数估计的方差都很小。参数估计的标准偏差是比方差更方便的度量，因为它与参数本身具有相同的单位，因此

$$Q_{H}(\mathcal{X}, \mathcal{Y}, \vec{p})=\sqrt{\max _{i=1}^{6} \lambda_{i}}$$
一个好的匹配应该给出一个小的正 $Q_H$ value。

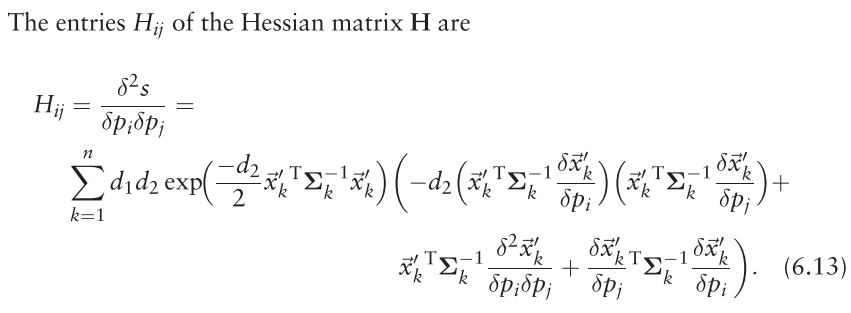
6.6.3 匹配的两个scan的点云对应的closest-point pairs的最小二范数度量

$$Q_{e}(\mathcal{X}, \mathcal{Y}, \vec{p})=\frac{1}{n} \sum_{i=1}^{n}\left\|\vec{x}_{i}-\vec{y}_{i}\right\|^{2}$$
一个好的匹配应该有比较小的正$Q_{e}$

6.6.4总结

得分和Hessian测量均取决于NDT cell大小。较小的cell size倾向于给出较小（接近于零）的分数值并且在参数估计中具有较小的变化。大cell中的分布通常更加分散，具有更大的差异。 另一方面，均方误差测量与NDT cell size无关。

图6.29显示了这三个质量度量如何对应于第6.4节中成对实验中使用的一些数据集的参考姿态的平移错误。所示结果是激光雷达扫描对的结果。在每种情况下，registration质量都是在0.5米的cell尺寸下进行评估的。所包含的图仅显示平移错误的置信度度量。检查相应的旋转误差图并不是很容易。在许多情况下，失败的注册在旋转误差中仍然只有一个小错误。另一方面，具有正确平移估计的注册结果只在旋转时出错是很不寻常的。因此，平移错误本身就是注册成功的一个很好的标志。可以看出，NDT评分函数和逆hessian矩阵的最大特征值与最终pose估计误差相当吻合。

对于所有的质量度量，在图中都可以看到注册Straight数据集的困难。例如，参见图6.29（b），其中显示了$Q_H$值。$Q_H$值与直线的最终平移误差只有微弱的相关性，这与此扫描对的误差分布沿隧道方向相当浅这一事实有关。然而，接近参考pose的QH值明显较低，并且与其他数据集相同的QH阈值（QH≤0.5），可用于区分失败注册和成功注册。

另一方面，平均平方点对点误差并不是衡量成功的一个很好的指标。首先，对于不同的扫描对，函数的输出值是不同的。例如，Straight数据集的值都在0.002和0.004之间，但Sci-Fi的值都在0.008以上——失败和成功。$Q_E$度量尤其是Straight和Sim-Mine数据集的registration质量指标，如图6.29（c）中缺乏相关性所示。在这两个扫描对的一些情况下，平移误差超过1米的pose比接近参考的姿态给出的$Q_E$值小。这一结果也解释了ICP在这两个扫描对上的表现不佳。图6.29（c）中的绘图没有离群值阈值，计算所有最近点对。如第6.4.2节和第6.4.3节中所述，使用0.5m离群值阈值进行ICP试验，得出类似结果。附录C.8中包含了显示kvarntro回路数据集扫描置信度测量值的数字。

不使用linked cell时，质量度量值不会发生显着变化，但如果单元格大小不同，则必须为Qs和QH度量选择另一个阈值。图6.30显示了Qs和QH如何随Sci-Fi数据集的不同小区大小而变化。该图显示最终pose估计的不确定性随着cell size的增大而增加，原因是先前描述的细节损失。对于超过2m的单元尺寸，Qs的值实际上恒定为高达0.5m的平移误差。在图6.30（b）的QH图中也可以看到相同的结果。比较图6.30中的Qs和QH，还可以看出QH是比Qs更好的置信度量。较低的QH值清楚地对应于登记结果的较高置信度。尽管当单元格大小时，并不总是可以选择区分良好注册与不良注册的阈值，但这只是在这些情况下注册结果更不确定的结果。相反，Qs得分值远离零并不一定对应于更好的结果

6.7 Conclusions

如第6.4节中的实验结果所示，NDT可用于快速和准确的3D扫描注册。使用NDT，不必在点或特征之间建立明确的对应关系。这是许多其他方法中最容易出错的部分。与经验丰富的研究人员进行的ICP实施相比，NDT更快，更可靠。与ICP相比，NDT的优势显示“扫描难度”最明显;也就是说，扫描具有很少的突出几何特征，很少的重叠和高噪声水平。

除了速度和准确性之外，NDT扫描注册还具有一些优于纯粹基于点云的方法（如ICP）的优势

• 一个是输出pose参数的方差和协方差的估计可以从registration期间使用的Hessian矩阵中立即获得，如第6.6节所示。registration后pose参数的方差可用于检测算法是否成功或者至少判断最终pose估计是否是可信的。此外，在SLAM设置中使用graph-based loop-closure算法时，重要的是获得与每个节点关联的pose vraiance值。
• 另一个优点是，与高分辨率点云相比，NDT需要很少的存储空间，同时保持扫描的3D表面较好的描述性。

总而言之，本章中提供的结果表明，NDT是用于通用3D扫描配准的良好表面表示。NDT表面表示对于其他应用也是有用的，如将在第III部分中详细描述的。

Chapter 7 Registration of coloured scans

Chapter8 Loop detection

这个部分记录简略一些，主要讲述ndt在回环检测方面的应用。主要思路是将每一个scan使用直方图来描述，然后将比较两个scan的相似程度转化为比较两个直方图的相似程度。

8.1 Surface-shape histograms

本章介绍的方法利用NDT表示创建紧凑但仍具有辨别力的外观描述符。为了最小化空间离散化的问题，使用重叠的NDT单元。 换句话说，如果每个单元的边长是B，则单元的中心点之间的距离是B / 2。 （参数选择将在8.1.4节中介绍。）

8.1.1 Appearance descriptor

• The covariance matrices $\mathbf{\Sigma}$ describe the shapes of the distributions.
• For each cell, compute the eigenvalues $\lambda_{1} \leq \lambda_{2} \leq \lambda_{3}$, corresponding eigenvectors $\vec{e}_{1}, \vec{e}_{2}, \vec{e}_{3}$ of $\mathbf{\Sigma}$

通过观察特征值的相对大小，可以看出三个主要的cell类别：spherical, planar, and linear。基于特征值与阈值$t_e \in [0,1]$之间的关系将distribution分成三类:

• linear if $\lambda_{2} / \lambda_{3} \leq t_{e}$
• planar if they are nonlinear and $\lambda_{1} / \lambda_{2} \leq t_{e}$
• spherical if they are nonlinear and nonplanar(in other words, if no eigenvalue is $1/t_e$ times larger than another one)

$t_e$是一个通过实验调试出来的经验值。分布显示图如下，

通过使用多个特征值比率阈值，可以直接使用更多类，例如不同级别的“几乎平面”分布。 但是，对于此处提供的数据，使用多个阈值$t_e$并未改善结果。

基于平面和线性类的取向(orientation for the planar and linear classes,)以及球形类的表面粗糙度(surface roughness for the spherical class)，可以将每个主单元类划分为subclasses。使用$n_s$球面子类，$n_p$平面子类和$n_l$线性子类，建议的外观描述符的基本元素是特征向量

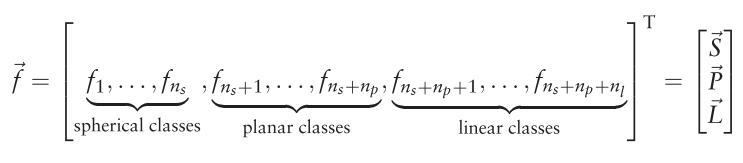
where $f_i$ is the number of occupied NDT cells that belong to class $i$（属于类别$i$的占用NDT cells的数量）

• Spherical subclasses be defined by "roundness" ratio $\lambda_{2} / \lambda_{3}$
  $$i=\left\lceil n_{s} \frac{\lambda_{2} / \lambda_{3}-t_{e}}{1-t_{e}}\right\rceil$$
  we have $t_{e}>\lambda_{2} / \lambda_{3} \geq 1$, so $1 ≤ i ≤ n_s$
• Planar
  最小的eigenvector $\vec{e}_{1}$将近似表示平面的法向量，用集合$\mathcal{P}=\left\{\pi_{1}, \dots, \pi_{n_{p}}\right\}$表示$n_p$个穿过原点的lines。
  $$i=n_{s}+\arg \min _{j} d\left(\vec{e}_{1}, \boldsymbol{\pi}_{j}\right)$$
  where $d(\vec{e}, \pi)$表示点$\vec e$和线$\boldsymbol{\pi}$的距离，in other words, index $i$ 就是距离$\vec e_1$最近的线$\boldsymbol{\pi_j}$的index $i$。
  均匀分布与原点相交的多条线的问题类似于在球体表面上均匀分布点，如下图所述，有必要使用一些启发式方法来生成近似均匀的点分布。 使用一种这样的算法在一个半球上分配$n_p$点。这里使用的线的分布在图8.1中可视化。P是连接原点和其中一个点的线组。
  
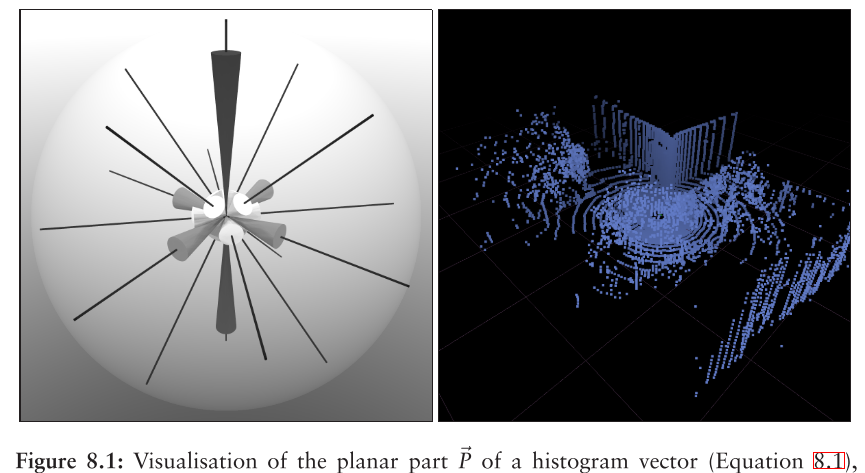
  在文章中$n_p$ = 9 planar directions are used.
  细黑线对应于方向$\pi_{1}, \dots, \pi_{9}$。 根据相应的直方图箱的值来缩放锥体。在该图中，每个方向有两个锥体：原点的每一侧有一个锥体。用于标准化扫描方向的主要方向是阴影。 （以下文字将在8.1.2节中进一步说明。）不在$\mathcal{D}_{1}$或$\mathcal{D}_{2}$中的方向为白色。在这种情况下，$\mathcal{D}_{1}$（深灰色）包含一个方向：垂直方向，对应于地平面。$\mathcal{D}_{2}$（浅灰色）包括两个潜在的次级峰值（其幅度更类似于其余的合并方向）。 在这个例子中，$t_a$设置为0.6。 如果$t_a$接近1，则D2将仅包括一个方向
• linear
  用于平面分布的相同方法也可用于线性分布,但是使用$\vec e_3$, 使用一个lines集合$\mathcal{L}=\left\{\boldsymbol{\lambda}_{1}, \dots, \boldsymbol{\lambda}_{n_{l}}\right\}$
  $$i=n_{s}+n_{l}+\underset{j}{\arg \min } d\left(\vec{e}_{3}, \boldsymbol{\lambda}_{j}\right)$$
  对于多种数据，planar比linear更具描述性，因此使用更多平面而不是线性子类可能更好。对于此处使用的实验，仅使用一个线性类就足够了。

Appearance Descriptor :
除了表面形状和方向之外，从扫描仪位置到特定表面的距离也是重要信息。 因此，每个scan由矩阵
$\mathbf{F}=\left[ \begin{array}{lll}{\vec{f}_{1}} & {\cdots} & {\vec{f}_{n_{r}}}\end{array}\right]$和相应的一组范围间隔$\mathcal{R}=\left\{\overline{r}_{1}, \ldots, \overline{r}_{n_{r}}\right\}$描述。矩阵是表面形状直方图组成，每一列$\vec{f}_{k}$是所有所有NDT cell（从激光扫描仪位置测量）在间隔$\overline{r}_{k}$下的直方图。

8.1.2 Rotation invariance

因为外观描述符（8.5）明确使用了表面的方向，所以它不是旋转不变的。为了使外观描述符对旋转不变，必须首先归一化扫描的方向。 本节介绍了在我们的实现中使用的获取旋转不变性的方法。
从初始柱状图向量$\vec{f^{'}}$开始，以单个范围间隔，$\mathcal{R}=\{[0, \infty)\}$，其思想是在平面方向上找到两个峰值，并确定扫描方向，使最常见的平面法向（主峰）沿着正Z轴对齐，第二个最常见的（次峰）位于YZ平面。使用平面取向而不是线取向的原因是平面单元比线性单元更常见

并非总是有一个明确的最大值，但可以使用两组方向，$\mathcal{D}_{1} \text { and } \mathcal{D}_{2}$。给定平面部分$\vec{P}^{\prime}=\left[P_{1}^{\prime}, \ldots, P_{n_{p}}^{\prime}\right]^{\mathrm{T}}$of $\vec{f^{'}}$, 一个模糊阈值$t_a\in[0，1]$决定了哪个柱状图更相似（该选择也在图8.1中说明）。首先，选取最大值的柱状图bin。

$$i^{\prime}=\underset{i}{\arg \max } P_{i}^{\prime}$$