PLSLAM: 基于点线综合特征的双目视觉

SLAM-VisualSLAM

---

Reference

• Paper: 基于点线综合特征的双目视觉
• Author: 谢晓佳（浙江大学硕士论文、SLAM大牛）
• Year: 2017

1 VLSAM中的线特征

1.1 线段特征的提取

LSD(Line Segment Detector)是一种能在线性时间内得到亚像素级精度的局部提取线段的算法，其核心思路是将梯度方向相近的像素点合并。

LineSegmentsDetection

pl-SLAM

1.2 线段特征的描述子

LBD_Descriptor

1.3 空间直线的参数化

空间点坐标 $\widetilde{\mathbf{X}}=[x, y, z]^{T}$
空间点的齐次坐标 $\mathbf{X}=[x, y, z, w]^{T}$, where $w=1$
面的齐次坐标 $\boldsymbol{\pi}=\left[\pi_{1}, \pi_{2}, \pi_{3}, \pi_{4}\right]^{T}$

• 空间点有4个自由度，空间刚体有6个自由度，减去1个沿着直线平移的自由度，再减去1个饶着直线旋转的自由度。
• 空间面有5个自由度，空间刚体有6个自由度，减去1个绕着平面法向量旋转的自由度。

1.3.1 空间直线方程表示(两个平面相交)

$$\left\{\begin{matrix} a_1x+b_1y+c_1z+1=0\\ a_2x+b_2y+c_2z+1=0 \end{matrix}\right.$$
也就是
$$\begin{bmatrix} a_1 &b_1 &c_1 &1 \\ a_2 &b_2 &c_2 &1 \end{bmatrix}\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}=0$$

1.3.2 直线上任意两点其次坐标构成直线

直线上任意两个点可以构成直线方程约束一条直线。将直线方程看成是两个空间点的齐次坐标，这两空间点的齐次坐标作为$\mathbf{w}$的行向量构成2×4矩阵：

$$\mathbf{w}=\left[\begin{array}{l}{\mathbf{x}_{1}^{\mathrm{T}}} \\ {\mathbf{x}_{2}^{\mathrm{T}}}\end{array}\right] = \begin{bmatrix} a_1 &b_1 &c_1 &1 \\ a_2 &b_2 &c_2 &1 \end{bmatrix}$$

然而这是一种非紧凑的表示，具有多余的4个参数，在优化问题中会引入额外的约束，在表达点线、线面相交以及相机投影时不太便利。这里引入其他两种空间直线的表示。

1.3.3 普吕克坐标

普吕克坐标由两空间点确定，其齐次坐标分别为$\mathbf{X}_{1}=\left(x_{1}, y_{1}, z_{1}, w_{1}\right)^{T}$和$\mathbf{X}_{2}=\left(x_{2}, y_{2}, z_{2}, w_{2}\right)^{T}$。
这个齐次坐标里面的$w$表示直线3维坐标的模，也就是

$$w=\sqrt{x^2+y^2+z^2}$$
首先定义普吕克矩阵如下：
$$\mathbf{L}=\mathbf{X}_{2} \mathbf{X}_{1}^{\mathrm{T}}-\mathbf{X}_{1} \mathbf{X}_{2}^{\mathrm{T}} \in \mathbb{R}^{4 \times 4} = \begin{bmatrix} 0 & x_2y_1-x_1y_2 &x_2z_1-x_1z_2 & x_2w_1-x_1w_2\\ -x_2y_1+x_1y_2 &0 &y_2z_1-y_1z_2 &y_2w_1-y_1w_2 \\ -x_2z_1+x_1z_2 & -y_2z_1+y_1z_2 &0 & z_2w_1-z_1w_2\\ -x_2w_1+x_1w_2 &-y_2w_1+y_1w_2 & -z_2w_1+z_1w_2 &0 \end{bmatrix}$$
代入计算，发现普吕克矩阵有特殊性质

• 是反对称矩阵，且对角元素均为0，只有6个有效非零元素 (6 DOF)
• $\operatorname{det}(\mathbf{L})=0$ (减去1 DOF)
• 取同一空间直线上任意两对空间点，它们对应的普吕克坐标只相差一个系数$\mathbf{L}=\alpha \mathbf{L}^{\prime}$(减去1 DOF)

根据以上性质，可以知道因为6个非零元素只有5个是有意义的，另外由于$\operatorname{det}(\mathbf{L})=0$，所以普吕克矩阵实际自由度为4。

普吕克坐标即由普吕克矩阵中6个非零的元素，将其按照一定的顺序排列成的一个六维向量，这里采用Bartoli论文中记号

$$\mathcal{L}=\left[\begin{array}{c}{\widetilde{\mathbf{X}}_{1} \times \widetilde{\mathbf{X}}_{2}} \\ {w_{1} \widetilde{\mathbf{X}}_{2}-w_{2} \widetilde{\mathbf{X}}_{1}}\end{array}\right]=\left[\begin{array}{l}{\mathbf{n}} \\ {\mathbf{v}}\end{array}\right] \in \mathbb{P}^{5} \subset \mathbb{R}^{6}$$

几何意义理解：

• $\mathcal{L}$中的元素由$\mathbf{L}$中的非零元素对应其中$\mathbf{v}$是直线的方向向量。
• 矩$\mathbf{n}$是过该直线且通过原点的平面的法向量，并且垂直于$\mathbf{v}$，即$\mathbf{n}^{\mathrm{T}} \mathbf{v}=0$，如下图所示。
• 原点到空间直线的垂直距离$\|\mathbf{n}\| /\|\mathbf{v}\|$，垂足$\mathbf{d}$的齐次坐标为$\left(\mathbf{v} \times \mathbf{n}, \mathbf{v}^{\mathrm{T}} \mathbf{v}\right)$

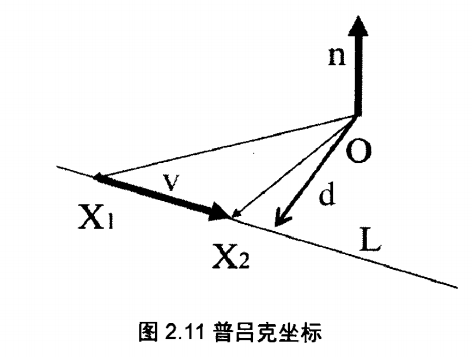
普吕克坐标与普吕克矩阵的关系如下：

$$\mathbf{L}=\left[\begin{array}{cc}{[\mathbf{n}]_{ \times}} & {\mathbf{v}} \\ {-\mathbf{v}^{\mathrm{T}}} & {0}\end{array}\right]$$

普吕克坐标在表达坐标变换和重投影时具有线性的形式，其中坐标变换的公式为

$$\left[\begin{array}{c}{\mathbf{n}_{c}} \\ {\mathbf{v}_{c}}\end{array}\right]=\left[\begin{array}{cc}{\mathbf{R}_{c w}} & {\left[\mathbf{t}_{c w}\right]_{ \times} \mathbf{R}_{c w}} \\ {\mathbf{0}} & {\mathbf{R}_{c w}}\end{array}\right]\left[\begin{array}{l}{\mathbf{n}_{w}} \\ {\mathbf{v}_{w}}\end{array}\right]$$
$$\left[\begin{array}{c}{\mathbf{n}_{w}} \\ {\mathbf{v}_{w}}\end{array}\right]=\left[\begin{array}{cc}{\mathbf{R}_{c w}^{\mathrm{T}}} & {-\mathbf{R}_{c w}^{\mathrm{T}}\left[\mathbf{t}_{c w}\right]_{ \times}} \\ {\mathbf{0}} & {\mathbf{R}_{c w}^{\mathrm{T}}}\end{array}\right]\left[\begin{array}{c}{\mathbf{n}_{c}} \\ {\mathbf{v}_{c}}\end{array}\right]$$

将空间直线投影到当前相机图像中，得到其投影直线方程为：

$$\mathbf{1}=\left[\begin{array}{l}{l_{1}} \\ {l_{2}} \\ {l_{3}}\end{array}\right]=\mathcal{K} \mathbf{n}^{c}=\left[\begin{array}{ccc}{f_{y}} & {0} & {0} \\ {0} & {f_{x}} & {0} \\ {-f_{y} c_{x}} & {-f_{x} c_{y}} & {f_{x} f_{y}}\end{array}\right] \mathbf{n}_{c}$$

这个推导过程很简单，就是比较繁琐，
空间直线上的两个点$\widetilde{\mathbf{X}}_{1}, \widetilde{\mathbf{X}}_{2}$变换到相机坐标系下得到$\widetilde{\mathbf{X}}_{c1}, \widetilde{\mathbf{X}}_{c2}$，这两个点也可以构成$\mathbf{n_c}$。
首先将相机坐标系下的两个点分别按照如下投影关系投影到相机平面，

$$[u,v]^T = \frac{1}{Z_c}[X_c,Y_c,Z_c]^T$$
得到两个二维平面点$[u_1,v_1]^T, [u_2, v_2]^T$，然后得到两点的平面直线方程，将方程统一成$l_1x+l_2y+l_3=0$的形式，就可以得到相机坐标系下直线投影到图像坐标系下的投影关系。

这里推导谢晓佳的硕士论文时，发现他的这个投影矩阵中第三行第二列少写了一个负号，在贺一家博士的PLVIO论文中印证了我的推导，hiahia，论推公式的重要性呀～

然而这种6参数的形式大于空间直线自由度，且存在正交约束，因此普吕克坐标是一种过参数化的表示。因此Bartoli提出了一种4参数的最小化表示方法，称之为正交表示。

1.3.4 直线参数化的正交表示

将$\mathbf{n,v}$组成如下曾广矩阵$\mathbf{[n|v]}$，然后进行QR矩阵分解如下：

$$[\mathbf{n} | \mathbf{v}]=\left[\frac{\mathbf{n}}{\|\mathbf{n}\|} \quad \frac{\mathbf{v}}{\|\mathbf{v}\|} \quad \frac{\mathbf{n} \times \mathbf{v}}{\|\mathbf{n} \times \mathbf{v}\|}\right]\left[\begin{array}{cc}{\|\mathbf{n}\|} & {0} \\ {0} & {\|\mathbf{v}\|} \\ {0} & {0}\end{array}\right] = \mathbf{U_{3x3}}\begin{bmatrix} w_1 & 0\\ 0 & w_2\\ 0 &0 \end{bmatrix}=[\mathbf{u_1} \mathbf{u_2} \mathbf{u_3}]\begin{bmatrix} w_1 & 0\\ 0 & w_2\\ 0 &0 \end{bmatrix}$$

令 $\mathbf{W}=\left[\begin{array}{cc}{\cos (\theta)} & {-\sin (\theta)} \\ {\sin (\theta)} & {\cos (\theta)}\end{array}\right]=\left[\begin{array}{cc}{w_{1}} & {-w_{2}} \\ {w_{2}} & {w_{1}}\end{array}\right]$， 其中$w_{1}, w_{2}>0$，对应的$\theta \in\left(0, \frac{\pi}{2}\right]$

正交表示可以很容易地转为普吕克坐标：

$$\mathcal{L}=\left[\begin{array}{l}{w_1 \mathbf{u}_{1}} \\ {w_2 \mathbf{u}_{2}}\end{array}\right]$$
其中$\mathbf{u_i}$表示矩阵$\mathbf{U}$的第$i$列。

空间直线的正交表示属于积流形(product manifold)，因此可以利用切空间上的元素定义其增量。设增量为

$$\delta_{\theta}=\begin{bmatrix} \theta_1\\ \theta_2\\ \theta_3\\ \theta \end{bmatrix}$$
前三个元素用于更新$\mathbf{U}$,最后一个元素用于更新$\mathbf{W}$
$$\left(\mathbf{U}^{*}, \mathbf{W}^{*}\right)=(\mathbf{U}, \mathbf{W}) \oplus \boldsymbol{\delta}_{\mathbf{\theta}}$$
其中,
$$\mathbf{U}^{*}=\exp \left(\boldsymbol{\theta}^{\wedge}\right) \mathbf{U}$$
$$\mathbf{W}^{*}=\left[\begin{array}{cc}{\cos (\theta)} & {-\sin (\theta)} \\ {\sin (\theta)} & {\cos (\theta)}\end{array}\right] \mathbf{W}$$

$\delta_{\theta}$中的4个参数具有具体的几何意义，$\mathbf{W}$隐含了$\mathbf{\frac{||n||}{||v||}}$的比值，也就是原点到空间直线的距离$d$，因此第4个参数$\theta$调节空间直线到远点的距离。距离确定的时候，$\theta$调节空间直线绕3个轴的旋转，在图中分别用橙色、绿色和蓝色的直线簇表示，其中黑色直线为更新前的空间直线。

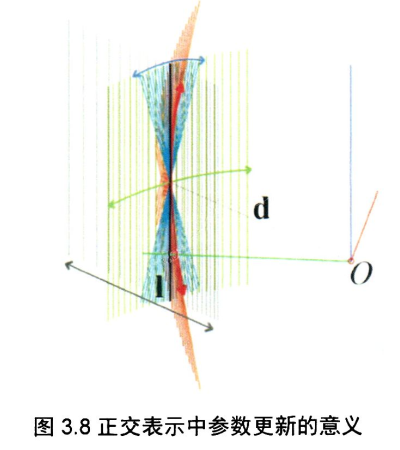
然而正交表示并不能像普吕克坐标一样很好地表示坐标变换和重投影，因此在本文中除了在后端优化中采用正交表示，其他情况下均采用普吕克坐标。

1.4 空间直线的观测模型

空间直线的观测模型存在多种定义方式，可以通过3D．3D的方式定义空间直线与匹配空间直线的误差，也可以通过3D．2D的方式定义空间直线与匹配图像直线的误差，通常采用后一种方法精度更高。

3D-2D的方式首先将空间直线重投影到图像上，然后计算投影直线$\mathbf{l^{'}}$和图像中的匹配线段$\mathbf{l}$的误差，图像中的线特征也可以用两个端点表示，分别为$\mathbf{X_s,X_e}$。
Bartoli列出了几种误差的定义方式，如

• 无几何意义的线性误差$e=1 \times 1^{\prime}$
• 代数距离定义的线性误差$e=[X_s^{T} l^{'},X_e^{T} l^{'}]^T$
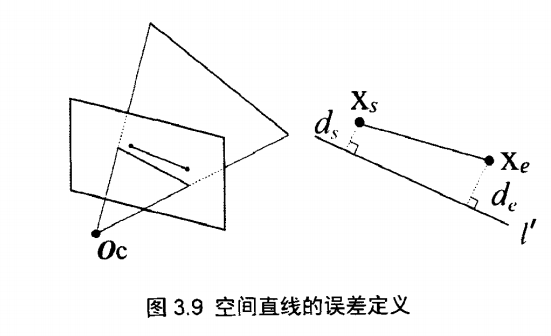
• 本文采用几何距离定义的非线性误差，其精度优于以上两种方法
  $$e=\left[\frac{\mathbf{x}_{s}^{\mathrm{T}} \mathbf{l}^{\prime}}{\sqrt{l_{1}^{2}+l_{2}^{2}}}, \frac{\mathbf{x}_{e}^{\mathrm{T}} \mathbf{l}^{\prime}}{\sqrt{l_{1}^{2}+l_{2}^{2}}}\right]^{\mathrm{T}}$$
  其中，$\mathbf{l}^{\prime}=\left[l_{1}, l_{2}, l_{3}\right]^{\mathrm{T}}$, $X_s=[u_s, v_s]^T， X_e=[u_e, v_e]^T$

由于孔径问题以及在连续帧的图像中空间直线端点不准确，只有匹配线段垂直于投影直线这部分才能提供有效信息，而平行于投影直线方向可能存在很大的误差，因此使用该模型作为观测模型是比较合理的。

2 点线综合的BA后端优化框架

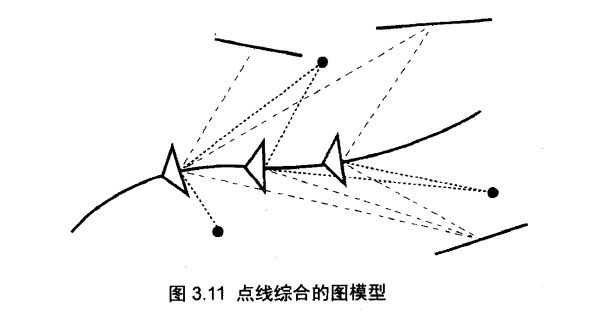
2.1 点线综合的图模型

下表总结三维点和空间直线的坐标变换和投影方程，采用了齐次坐标的表示使得式子更加简洁，其中第三行表示将空间特征投影到双目的右图像中

将三维点和空间直线进行重投影后的结果如图

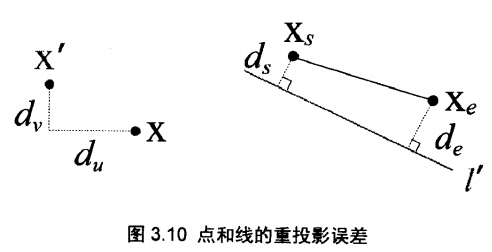
这两种误差的表示形式如下：

$$\begin{aligned} \boldsymbol{e} \boldsymbol{p}_{k, i} &=\mathbf{x}_{k, i}-\mathbf{n}\left(\mathbf{K} \mathbf{T}_{k w} \mathbf{X}_{w, i}\right) \\ \boldsymbol{e} \boldsymbol{l}_{k, j} &=\mathrm{d}\left(\mathbf{z}_{k, j}, \mathcal{K} \mathcal{H}_{c w} \boldsymbol{L}_{w, j}\right) \end{aligned}$$

在假设观测误差为高斯分布的情况下，可以得到最后的代价函数：

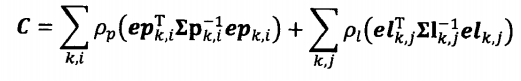
2.2 点线误差的雅可比矩阵

2.2.1 点误差关于位姿和三维点的雅克比矩阵

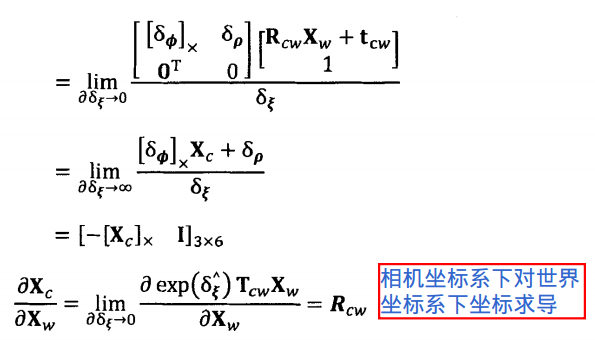
2.2.2 线误差关于位姿的雅克比矩阵

需要求解直线重投影误差关于位姿增量$\delta_{\xi}$和空间直线正交表示增量$\delta_{\boldsymbol{\theta}}$的雅可比矩阵。
求导思路是使用链式法则

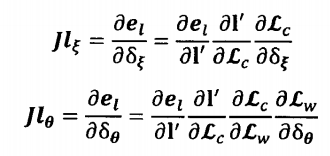
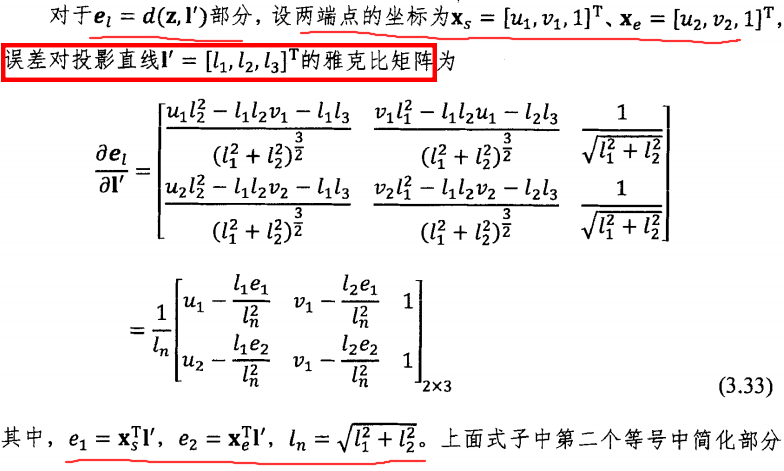
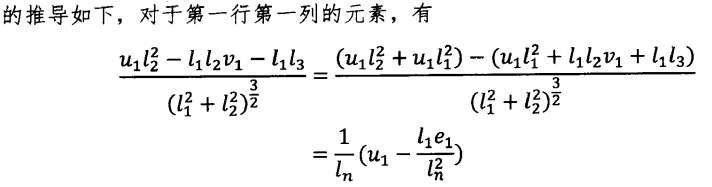
这里直接给出结果，详细推导请参看该论文

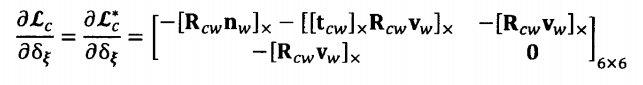
３点线综合的视觉词典

这里使用ORB点特征描述子和LBD直线特征描述子，由于它们都是256位的二进制描述子，因此把它们放在同一个视觉词典里，可以简化建立视觉字典的过程以及进行回环检测时所进行的操作。通常图像中的点特征多和线特征少，点线特征在视觉词典里要区别对待，因此为ORB描述子添加标志位0，为LBD描述子添加标志位1，用标志位便可区分点特征与直线特征。

这个地方涉及到回环问题，先占坑。。。。。。。。。。。。。。

4 PL-SLAM系统框架和细节

基于ORB-SLAM