costmap_2d —— bresenham快速画直线算法

navigation

---

Reference

• Bresenham直线算法与画圆算法
• The Bresenham Line-Drawing Algorithm
• wiki

1 bresenham快速画直线算法

　　Bresenham直线算法是用来描绘由两点所决定的直线的算法，它会算出一条线段在 n 维光栅上最接近的点。这个算法只会用到较为快速的整数加法、减法和位元移位，常用于绘制电脑画面中的直线。是计算机图形学中最先发展出来的算法。

1.1 计算机是如何画直线的？

简单来说，如下图所示，真实的直线是连续的，但我们的计算机显示的精度有限，不可能真正显示连续的直线，于是我们用一系列离散化后的点（像素）来近似表现这条直线。

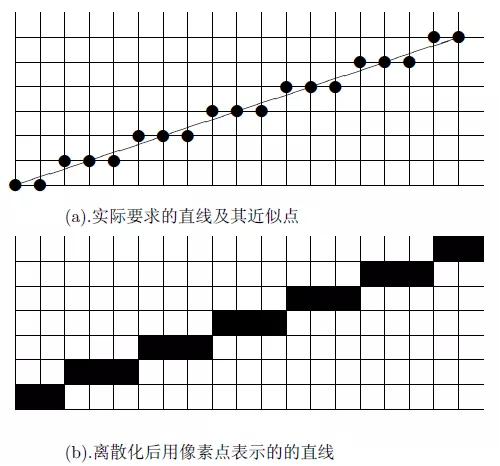
1.2 画直线的算法分析

考虑最简单的情况，$x_1<x_2, y_1<y_2, k=\frac{y_2-y_1}{x_2-x_1} \in [0, 1]$

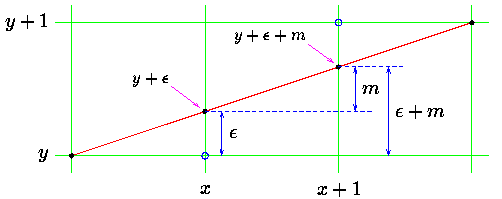
算法流程如下

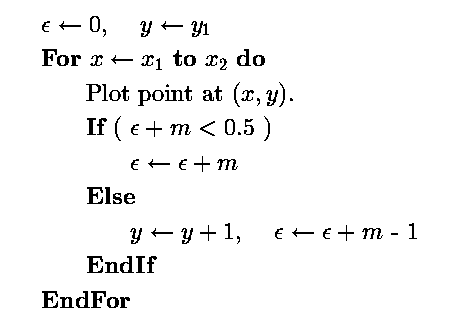
核心理解点是

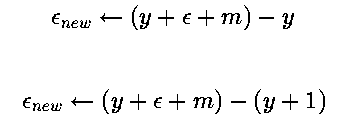
考虑第二种情况,$x_1<x_2, y_1<y_2, k=\frac{y_2-y_1}{x_2-x_1} \in [-1, 0]$

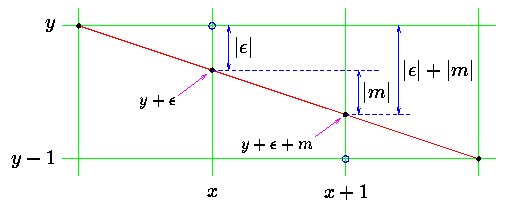
算法流程如下

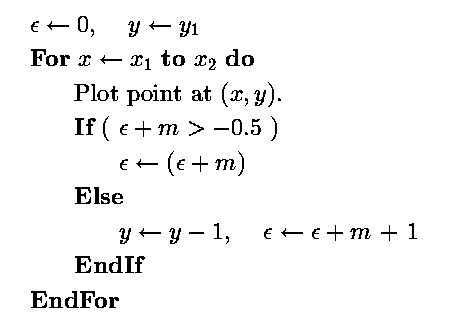
核心理解点是

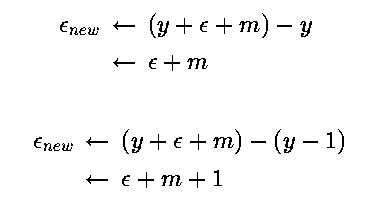
事实上要根据起始点终点画一条直线(按照带箭头的理解)一共有八种情况

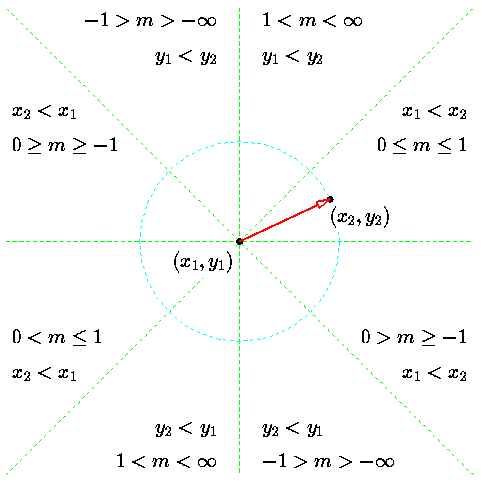
我们通过一个简单的处理将八种情况都统一到上面的两种情况来处理，思路是：

• 上面两种处理的都是小斜率情况，也就是$|k| \in [0, 1]$,如果要处理大斜率情况，可以通过交换$x,y$值得到，相当于进行了$x,y$坐标轴的互换，但是plot的时候要注意，要交换过来
• 上面两种情况处理的的都是$x$递增的情况，如果$x$是递减的，可以通过交换起点和终点

1.3 一般化的完整算法(涵盖八种情况的处理)

function draw_line(x0,x1,y0,y1)
    steep = abs(y1-y0)>abs(x1-x0) //判断是否是大斜率情况
    if steep then //处理大斜率情况，交换x,y坐标
        swap(x0,y0)
        swap(x1,y1)
    if x0>x1 then //处理x递减的情况，交换起点和终点
        swap(x0,x1)
        swap(y0,y1)
    int deltx = x1-x0      //+
    int delty = abs(y1-y0) //+
    double error = 0       //误差+
    double delterr = deltay/deltx //斜率+
    int y = y0  //画线y坐标
    int ystep   //应对 1.2 中介绍的两种情况
    if y0<y1 then
        ystep = 1
    else
        ystep = -1
    for x from x0 to x1 //画线x坐标
        if steep then 
            plot(y,x)//大斜率
        else 
            plot(x,y)
        error =  error + delterr
        if error >=0.5 then //这个地方将上面的两种情况又统一成了一种情况，niubility啊！
            y = y + ystep
            error = error -1

接下来解释一下为什么可以将上面的两种情况统一
第二种情况的判断条件是，$\epsilon+m<=-0.5$，其中 $\epsilon<0, m<0$,
写成

$$-\epsilon-m >= 0.5$$
更新条件是
$$y \leftarrow y-1, \quad \epsilon \leftarrow \epsilon+m+1$$
写成
$$y \leftarrow y-1, \quad -\epsilon \leftarrow -\epsilon-m-1$$
所以
$$error = -\epsilon, delterr = -m$$

1.4 最佳化(所有的浮点计算全部转为整数运算)

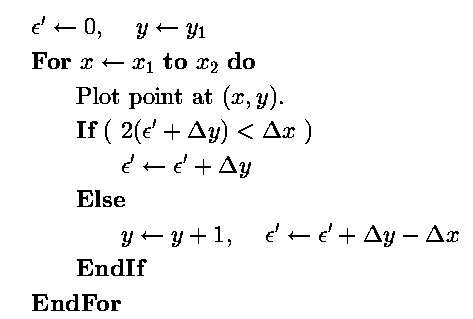
 function line(x0, x1, y0, y1)
     boolean steep := abs(y1 - y0) > abs(x1 - x0)
     if steep then
         swap(x0, y0)
         swap(x1, y1)
     if x0 > x1 then
         swap(x0, x1)
         swap(y0, y1)
     int deltax := x1 - x0
     int deltay := abs(y1 - y0)
     int error := deltax / 2
     int ystep
     int y := y0
     if y0 < y1 then ystep := 1 else ystep := -1
     for x from x0 to x1
         if steep then plot(y,x) else plot(x,y)
         error := error - deltay
         if error < 0 then
             y := y + ystep
             error := error + deltax

理解这个算法转换的核心是将判断条件$2\left(\epsilon^{\prime}+\Delta y\right)>=\Delta x$，写成

$$\Delta x/2-\Delta y - \epsilon^{\prime} <=0$$
所以$y \leftarrow y+1, \quad \epsilon^{\prime} \leftarrow \epsilon^{\prime}+\Delta y-\Delta x$，写成
$$y \leftarrow y+1, \quad -\epsilon^{\prime} \leftarrow -\epsilon^{\prime}-\Delta y+\Delta x$$
误差写成
$$error = -\epsilon^{\prime} , 初始化为 \Delta x/2$$

2 应用

在珊格地图中，已知起止点（当前激光束测量数据）就可以使用bresenham算法得到两点之间的通过点，进而利用概率知识更新对应格子的概率值，得到珊格地图。