[关闭]
@iStarLee 2019-08-13T05:46:21.000000Z 字数 13304 阅读 875

GlobalPlanner —— A*算法

navigation

Reference

1 Introduction

1.1 常见路径搜索算法

1.2 A*的一个简单描述

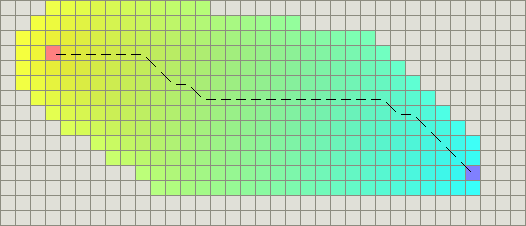
在凹型障碍物的例子中，A*找到一条和Dijkstra算法一样好的路径：
image_1dhvnkjvgeb71n5s15o07lqebn9.png-7.2kB

成功的秘决在于，它把Dijkstra算法（靠近初始点的结点）和BFS算法（靠近目标点的结点）的信息块结合起来。在讨论A*的标准术语中

在上图中，

当从初始点向目标点移动时，A*权衡这两者。每次进行主循环时，它检查f(n)最小的结点n，其中f(n) = g(n) + h(n)。

2 启发式算法

启发式函数h(n)告诉A*从任意结点n到目标结点的最小代价评估值。

2.1 A*对启发式函数的使用

启发式函数可以控制A*的行为：

所以我们得到一个很有趣的情况，那就是我们可以决定我们想要从A*中获得什么。理想情况下（注：原文为At exactly the right point），我们想最快地得到最短路径。如果我们的目标太低，我们仍会得到最短路径，不过速度变慢了；如果我们的目标太高，那我们就放弃了最短路径，但A*运行得更快。

A*的这个特性非常有用。例如，你会发现在某些情况下，你希望得到一条好的路径（"good" path）而不是一条完美的路径（"perfect" path）。为了权衡g(n)和h(n)，你可以修改任意一个。

在学术上，如果启发式函数值是对实际代价的低估，A*算法被称为简单的A算法（原文为simply A）。然而，我继续称之为A*，因为在实现上是一样的，并且在游戏编程领域并不区别A和A*。

2.2 速度还是精确度？

速度和精确度之间的选择前不是静态的。你可以基于CPU的速度、用于路径搜索的时间片数、地图上物体（units）的数量、物体的重要性、组（group）的大小、难度或者其他任何因素来进行动态的选择。取得动态的折衷的一个方法是，建立一个启发式函数用于假定通过一个网格空间的最小代价是1，然后建立一个代价函数（cost function）用于测量（scales）：

速度和精确度之间的选择并不是全局的。在地图上的某些区域，精确度是重要的，你可以基于此进行动态选择。
在安全区域，可以考虑不寻找精确的最短路径而取近似路径，因此寻路快；但在危险区域，逃跑的安全性和逃跑速度是重要的，即路径的精确度是重要的，因此可以多花点时间用于寻找精确路径。

2.3 衡量单位

A*计算f(n) = g(n) + h(n)。为了对这两个值进行相加，这两个值必须使用相同的衡量单位。如果g(n)用小时来衡量而h(n)用米来衡量，那么A*将会认为g或者h太大或者太小，因而你将不能得到正确的路径，同时你的A*算法将运行得更慢。

2.4 精确的启发式函数

　　如果你的启发式函数精确地等于实际最佳路径（optimal path），如下一部分的图中所示，你会看到此时A*扩展的结点将非常少。A*算法内部发生的事情是：在每一结点它都计算f(n) = g(n) + h(n)。当h(n)精确地和g(n)匹配（译者注：原文为match）时，f(n)的值在沿着该路径时将不会改变。不在正确路径（right path）上的所有结点的f值均大于正确路径上的f值（译者注：正确路径在这里应该是指最短路径）。如果已经有较低f值的结点，A*将不考虑f值较高的结点，因此它肯定不会偏离最短路径。

2.4.1 预计算的精确启发式函数

　　构造精确启发函数的一种方法是预先计算任意一对结点之间最短路径的长度。在许多游戏的地图中这并不可行。然后，有几种方法可以近似模拟这种启发函数：

然后添加一个启发函数h’用于评估从任意位置到达邻近导航点（waypoints）的代价。（如果愿意，后者也可以通过预计算得到。）最终的启发式函数可以是：

或者如果你希望一个更好但是更昂贵的启发式函数，则分别用靠近结点和目标的所有的w1,w2对对上式进行求值。（译者注：原文为or if you want a better but more expensive heuristic, evaluate the above with all pairs w1, w2 that are close to the node and the goal, respectively.）

2.4.2 线性精确启发式算法

　　在特殊情况下，你可以不通过预计算而让启发式函数很精确。如果你有一个不存在障碍物和slow地形，那么从初始点到目标的最短路径应该是一条直线。

　　如果你正使用简单的启发式函数（我们不知道地图上的障碍物），则它应该和精确的启发式函数相符合（译者注：原文为match）。如果不是这样，则你会遇到衡量单位的问题，或者你所选择的启发函数类型的问题。

2.5 网格地图中的启发式算法

　　在网格地图中，有一些众所周知的启发式函数。

2.5.1 曼哈顿距离

标准的启发式函数是曼哈顿距离（Manhattan distance）。考虑你的代价函数并找到从一个位置移动到邻近位置的最小代价D，因此，我的游戏中的启发式函数应该是曼哈顿距离的D倍：

  1.     // 曼哈顿距离
  2.     H(n) = D * (abs ( n.x – goal.x ) + abs ( n.y – goal.y ) )

你应该使用符合你的代价函数的衡量单位。

image_1dhvostst1b2613g61mfo1pgftmnm.png-11.7kB

曼哈顿距离又称为出租车距离，曼哈顿距离不是距离不变量，当坐标轴变动时，点间的距离就会不同

2.5.2 对角线距离

如果在你的地图中你允许对角运动那么你需要一个不同的启发函数。（4 east, 4 north）的曼哈顿距离将变成8*D。然而，你可以简单地移动（4 northeast）代替，所以启发函数应该是4*D。这个函数使用对角线，假设直线和对角线的代价都是D：

  1.     // 对角线距离
  2.     h(n) = D * max(abs(n.x - goal.x), abs(n.y - goal.y))

image_1dhvp6guitnc18bq1np317rl1gn13.png-6kB

如果对角线运动的代价不是D，但类似于D2 = sqrt(2) *D，则上面的启发函数不准确。你需要一些更准确（原文为sophisticated）的东西：

  1. // 计算h_diagonal(n)：沿着斜线可以移动的步数
  2. h_diagonal(n) = min(abs(n.x - goal.x), abs(n.y - goal.y))
  3. // h_straight(n)：曼哈顿距离
  4. h_straight(n) = (abs(n.x - goal.x) + abs(n.y - goal.y))
  5. // 然后合并这两项，让所有的斜线步都乘以D2，剩下的所有直线步(注意这里是曼哈顿距离的步数减去2倍的斜线步数)都乘以D
  6. h(n) = D2 * h_diagonal(n) + D * (h_straight(n) - 2*h_diagonal(n)))

2.5.3 欧几里得距离

如果你的单位可以沿着任意角度移动（而不是网格方向），那么你也许应该使用直线距离：

  1. h(n) = D * sqrt((n.x-goal.x)^2 + (n.y-goal.y)^2)

然而，如果是这样的话，直接使用A*时将会遇到麻烦，因为代价函数g不会match启发函数h。因为欧几里得距离比曼哈顿距离和对角线距离都短，你仍可以得到最短路径，不过A*将运行得更久一些：
image_1dhvpcufl18pa7tv2nmjg1bp41g.png-7.4kB

2.5.4 平方后的欧几里得距离

我曾经看到一些A*的网页，其中提到让你通过使用距离的平方而避免欧几里得距离中昂贵的平方根运算：

  1. // THIS is wrong!
  2. h(n) = D * ((n.x-goal.x)^2 + (n.y-goal.y)^2)

不要这样做！这明显地导致衡量单位的问题。当A*计算f(n) = g(n) + h(n)，距离的平方将比g的代价大很多，并且你会因为启发式函数评估值过高而停止。对于更长的距离，这样做会靠近g(n)的极端情况而不再计算任何东西，A*退化成BFS：

2.5.5 Breaking ties

2.5.6 区域搜索

　　如果你想搜索邻近目标的任意不确定结点，而不是某个特定的结点，你应该建立一个启发函数h’(x)，使得h’(x)为h1(x), h2(x), h3(x)。。。的最小值，而这些h1, h2, h3是邻近结点的启发函数。然而，一种更快的方法是让A*仅搜索目标区域的中心。一旦你从OPEN集合中取得任意一个邻近目标的结点，你就可以停止搜索并建立一条路径了。

3 Implementation notes

3.1 算法流程

3.1.1 基本概念总结

3.1.2 算法解析

算法流程参看的是geeksforgeeks,这个上面的是英文写的，但是都比较浅显，非常容易理解。

  1. // A* Search Algorithm
  2. 1.  Initialize the open list
  3. 2.  Initialize the closed list
  4.     put the starting node on the open 
  5.     list (you can leave its f at zero)
  7. 3.  while the open list is not empty
  8.     a) find the node with the least f on 
  9.        the open list, call it "q"
  11.     b) pop q off the open list
  13.     c) generate q's 8 successors and set their 
  14.        parents to q
  16.     d) for each successor
  17.         i) if successor is the goal, stop search
  18.           successor.g = q.g + distance between 
  19.                               successor and q
  20.           successor.h = distance from goal to 
  21.           successor (This can be done using many 
  22.           ways, we will discuss three heuristics- 
  23.           Manhattan, Diagonal and Euclidean 
  24.           Heuristics)
  26.           successor.f = successor.g + successor.h
  28.         ii) if a node with the same position as 
  29.             successor is in the OPEN list which has a 
  30.            lower f than successor, skip this successor
  32.         iii) if a node with the same position as 
  33.             successor  is in the CLOSED list which has
  34.             a lower f than successor, skip this successor
  35.             otherwise, add  the node to the open list
  36.      end (for loop)
  38.     e) push q on the closed list
  39.     end (while loop)

3.2 算法实现

我根据上面的代码理解，修改了一下代码，代码量减少了很多

  1. // A C++ Program to implement A* Search Algorithm 
  2. #include<bits/stdc++.h>
  3. using namespace std;
  5. #define ROW 9
  6. #define COL 10
  8. // Creating a shortcut for int, int pair type 
  9. typedef pair<int, int> Pair;
  11. // Creating a shortcut for pair<int, pair<int, int>> type 
  12. typedef pair<double, pair<int, int>> pPair;
  14. // A structure to hold the neccesary parameters 
  15. struct cell {
  16.     // Row and Column index of its parent
  17.     // Note that 0 <= i <= ROW-1 & 0 <= j <= COL-1
  18.     int parent_i, parent_j;
  19.     // f = g + h
  20.     double f, g, h;
  21. };
  23. // A Utility Function to check whether given cell (row, col) 
  24. // is a valid cell or not. 
  25. bool isValid(int row, int col)
  26. {
  27.     // Returns true if row number and column number
  28.     // is in range
  29.     return (row >= 0) && (row < ROW) &&
  30.            (col >= 0) && (col < COL);
  31. }
  33. // A Utility Function to check whether the given cell is 
  34. // blocked or not 
  35. bool isUnBlocked(int grid[][COL], int row, int col)
  36. {
  37.     // Returns true if the cell is not blocked else false
  38.     if (grid[row][col] == 1)
  39.         return (true);
  40.     else
  41.         return (false);
  42. }
  44. // A Utility Function to check whether destination cell has 
  45. // been reached or not 
  46. bool isDestination(int row, int col, Pair dest)
  47. {
  48.     if (row == dest.first && col == dest.second)
  49.         return (true);
  50.     else
  51.         return (false);
  52. }
  54. // A Utility Function to calculate the 'h' heuristics. 
  55. double calculateHValue(int row, int col, Pair dest)
  56. {
  57.     // Return using the distance formula
  58.     return ((double) sqrt((row - dest.first)*(row - dest.first)
  59.                           + (col - dest.second)*(col - dest.second)));
  60. }
  62. // A Utility Function to trace the path from the source 
  63. // to destination 
  64. void tracePath(cell cellDetails[][COL], Pair dest)
  65. {
  66.     printf("\nThe Path is ");
  67.     int row = dest.first;
  68.     int col = dest.second;
  70.     stack<Pair> Path;
  72.     while (!(cellDetails[row][col].parent_i == row
  73.              && cellDetails[row][col].parent_j == col))
  74.     {
  75.         Path.push(make_pair(row, col));
  76.         int temp_row = cellDetails[row][col].parent_i;
  77.         int temp_col = cellDetails[row][col].parent_j;
  78.         row = temp_row;
  79.         col = temp_col;
  80.     }
  82.     Path.push(make_pair(row, col));
  83.     while (!Path.empty())
  84.     {
  85.         pair<int, int> p = Path.top();
  86.         Path.pop();
  87.         printf("-> (%d,%d) ", p.first, p.second);
  88.     }
  90.     return;
  91. }
  93. // traversing neighbors
  94. bool TraversingEightNeighbors(cell cellDetails[][COL], Pair dest,
  95.                               bool closedList[][COL], int grid[][COL],
  96.                               set<pPair> &openList, bool &foundDest, int i, int j)
  97. {
  98. /*
  99.             Generating all the 8 successor of this cell
  101.             N.W   N   N.E
  102.                \  |  /
  103.                 \ | /
  104.             W----Cell----E
  105.                 / | \
  106.                /  |  \
  107.             S.W   S   S.E
  109.             Cell-->Popped Cell (i, j)
  110.             N --> North  (i-1, j)
  111.             S --> South  (i+1, j)
  112.             E --> East   (i, j+1)
  113.             W --> West       (i, j-1)
  114.             N.E--> North-East (i-1, j+1)
  115.             N.W--> North-West (i-1, j-1)
  116.             S.E--> South-East (i+1, j+1)
  117.             S.W--> South-West (i+1, j-1)*/
  118.     vector<pair<int, int>> neighborsIndex = {make_pair(i - 1, j),
  119.                                              make_pair(i + 1, j),
  120.                                              make_pair(i, j + 1),
  121.                                              make_pair(i, j - 1),
  122.                                              make_pair(i - 1, j + 1),
  123.                                              make_pair(i - 1, j - 1),
  124.                                              make_pair(i + 1, j + 1),
  125.                                              make_pair(i + 1, j - 1)};
  126.     for (int ind = 0; ind < neighborsIndex.size(); ++ind)
  127.     {
  128.         int ni = neighborsIndex[ind].first;
  129.         int nj = neighborsIndex[ind].second;
  131.         // Only process this cell if this is a valid one
  132.         if (isValid(ni, nj) == true)
  133.         {
  134.             // If the destination cell is the same as the
  135.             // current successor
  136.             if (isDestination(ni, nj, dest) == true)
  137.             {
  138.                 // Set the Parent of the destination cell
  139.                 cellDetails[ni][nj].parent_i = i;
  140.                 cellDetails[ni][nj].parent_j = j;
  141.                 printf("The destination cell is found\n");
  142.                 tracePath(cellDetails, dest);
  143.                 foundDest = true;
  144.                 return true;
  145.             }
  146.                 // If the successor is already on the closed
  147.                 // list or if it is blocked, then ignore it.
  148.                 // Else do the following
  149.             else if (closedList[ni][nj] == false && isUnBlocked(grid, ni, nj) == true)
  150.             {
  151.                 // To store the 'g', 'h' and 'f' of the 8 successors
  152.                 double gNew = cellDetails[i][j].g + 1.0;
  153.                 double hNew = calculateHValue(ni, nj, dest);
  154.                 double fNew = gNew + hNew;
  156.                 // If it isn’t on the open list, add it to
  157.                 // the open list. Make the current square
  158.                 // the parent of this square. Record the
  159.                 // f, g, and h costs of the square cell
  160.                 //           OR
  161.                 // If it is on the open list already, check
  162.                 // to see if this path to that square is better,
  163.                 // using 'f' cost as the measure.
  164.                 if (cellDetails[ni][nj].f == FLT_MAX ||
  165.                     cellDetails[ni][nj].f > fNew)
  166.                 {
  167.                     openList.insert(make_pair(fNew, make_pair(ni, nj)));
  169.                     // Update the details of this cell
  170.                     cellDetails[ni][nj].f = fNew;
  171.                     cellDetails[ni][nj].g = gNew;
  172.                     cellDetails[ni][nj].h = hNew;
  173.                     cellDetails[ni][nj].parent_i = i;
  174.                     cellDetails[ni][nj].parent_j = j;
  175.                 }
  176.             }
  177.         }
  178.     }
  180.     return false;
  181. }
  183. // A Function to find the shortest path between 
  184. // a given source cell to a destination cell according 
  185. // to A* Search Algorithm 
  186. void aStarSearch(int grid[][COL], Pair src, Pair dest)
  187. {
  188.     // If the source is out of range
  189.     if (isValid(src.first, src.second) == false)
  190.     {
  191.         printf("Source is invalid\n");
  192.         return;
  193.     }
  195.     // If the destination is out of range
  196.     if (isValid(dest.first, dest.second) == false)
  197.     {
  198.         printf("Destination is invalid\n");
  199.         return;
  200.     }
  202.     // Either the source or the destination is blocked
  203.     if (isUnBlocked(grid, src.first, src.second) == false ||
  204.         isUnBlocked(grid, dest.first, dest.second) == false)
  205.     {
  206.         printf("Source or the destination is blocked\n");
  207.         return;
  208.     }
  210.     // If the destination cell is the same as source cell
  211.     if (isDestination(src.first, src.second, dest) == true)
  212.     {
  213.         printf("We are already at the destination\n");
  214.         return;
  215.     }
  217.     // Create a closed list and initialise it to false which means
  218.     // that no cell has been included yet
  219.     // This closed list is implemented as a boolean 2D array
  220.     bool closedList[ROW][COL];
  221.     memset(closedList, false, sizeof(closedList));
  223.     // Declare a 2D array of structure to hold the details
  224.     //of that cell
  225.     cell cellDetails[ROW][COL];
  227.     int i, j;
  229.     for (i = 0; i < ROW; i++)
  230.     {
  231.         for (j = 0; j < COL; j++)
  232.         {
  233.             cellDetails[i][j].f = FLT_MAX;
  234.             cellDetails[i][j].g = FLT_MAX;
  235.             cellDetails[i][j].h = FLT_MAX;
  236.             cellDetails[i][j].parent_i = -1;
  237.             cellDetails[i][j].parent_j = -1;
  238.         }
  239.     }
  241.     // Initialising the parameters of the starting node
  242.     i = src.first, j = src.second;
  243.     cellDetails[i][j].f = 0.0;
  244.     cellDetails[i][j].g = 0.0;
  245.     cellDetails[i][j].h = 0.0;
  246.     cellDetails[i][j].parent_i = i;
  247.     cellDetails[i][j].parent_j = j;
  249.     /*
  250.     Create an open list having information as-
  251.     <f, <i, j>>
  252.     where f = g + h,
  253.     and i, j are the row and column index of that cell
  254.     Note that 0 <= i <= ROW-1 & 0 <= j <= COL-1
  255.     This open list is implenented as a set of pair of pair.*/
  256.     set<pPair> openList;
  258.     // Put the starting cell on the open list and set its
  259.     // 'f' as 0
  260.     openList.insert(make_pair(0.0, make_pair(i, j)));
  262.     // We set this boolean value as false as initially
  263.     // the destination is not reached.
  264.     bool foundDest = false;
  266.     while (!openList.empty())
  267.     {
  268.         // Find the node with the least f on the open list
  269.         pPair p = *openList.begin();
  271.         // Remove this vertex from the open list
  272.         openList.erase(openList.begin());
  274.         // Add this vertex to the closed list
  275.         i = p.second.first;
  276.         j = p.second.second;
  277.         closedList[i][j] = true;
  279.         // if find destination, return
  280.         if (TraversingEightNeighbors(cellDetails, dest, closedList, grid,
  281.                 openList, foundDest, i, j))
  282.             return;
  283.     }
  285.     // When the destination cell is not found and the open
  286.     // list is empty, then we conclude that we failed to
  287.     // reach the destiantion cell. This may happen when the
  288.     // there is no way to destination cell (due to blockages)
  289.     if (foundDest == false)
  290.         printf("Failed to find the Destination Cell\n");
  292.     return;
  293. }
  296. // Driver program to test above function 
  297. int main()
  298. {
  299.     /* Description of the Grid-
  300.     1--> The cell is not blocked
  301.     0--> The cell is blocked */
  302.     int grid[ROW][COL] =
  303.             {
  304.                     {1, 0, 1, 1, 1, 1, 0, 1, 1, 1},
  305.                     {1, 1, 1, 0, 1, 1, 1, 0, 1, 1},
  306.                     {1, 1, 1, 0, 1, 1, 0, 1, 0, 1},
  307.                     {0, 0, 1, 0, 1, 0, 0, 0, 0, 1},
  308.                     {1, 1, 1, 0, 1, 1, 1, 0, 1, 0},
  309.                     {1, 0, 1, 1, 1, 1, 0, 1, 0, 0},
  310.                     {1, 0, 0, 0, 0, 1, 0, 0, 0, 1},
  311.                     {1, 0, 1, 1, 1, 1, 0, 1, 1, 1},
  312.                     {1, 1, 1, 0, 0, 0, 1, 0, 0, 1}
  313.             };
  315.     // Source is the left-most bottom-most corner
  316.     Pair src = make_pair(8, 0);
  318.     // Destination is the left-most top-most corner
  319.     Pair dest = make_pair(0, 0);
  321.     aStarSearch(grid, src, dest);
  323.     return (0);
  324. }

3.3 算法总结

  1. cellDetails[ni][nj].parent_i = i;
  2. cellDetails[ni][nj].parent_j = j;

所以回溯路径的判断条件是

  1. //最终row和col会达到初始点的位置
  2.     while (!(cellDetails[row][col].parent_i == row
  3.              && cellDetails[row][col].parent_j == col))
  4.     {
  5.         Path.push(make_pair(row, col));
  6.         int temp_row = cellDetails[row][col].parent_i;
  7.         int temp_col = cellDetails[row][col].parent_j;
  8.         row = temp_row;
  9.         col = temp_col;
  10.     }
添加新批注
在作者公开此批注前，只有你和作者可见。
回复批注