超定方程的解法

Optimization

1 最小二乘法求解

2 转化为正规方程组求解

对于方程组Ax=b，A为n×m矩阵，如果A列满秩，且n>m。则方程组没有精确解，此时称方程组为超定方程组。

2.1 线性非齐次方程组$Ax=b，b \not=0$

对于超定方程组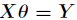
做以下操作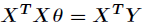
则求解转化为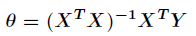
证明详细看这篇文章——矩阵求导解最小二乘问题

最小二乘法  在matlab中  可以直接$x=A$ \ $b$，自己一般习惯$x=(A'*A)$ \ $(A*b)$，两者在matlab中处理方法是一样的即最小二乘法。

2.2 线性齐次方程组Ax=0

一般用svd分解，后者是求解特征后，得到最小的特征值对应的特征向量为方程组的解，解会有很多组，可以选取归一化的那组。当然方程组一般是超定的，应该应经过A'*A处理。

2.3 非线性方程组

levenlerg-marquaerdt，牛顿法等，前者用得比较多，在matlab中用lsqnonlin函数进行求解.

齐次线性方程组的解、SVD、最小二乘法