Decision Tree

给我写信
GitHub

数据挖掘&机器学习

目录

信息论基础

---

对于包含以下4个符号的系统，A, B, C, D，我们可以有多种方法对其进行编码。例如：

方法1：

符号	编码	出现概率
A	00	0.1
B	01	0.2
C	10	0.2
D	11	0.5

方法2：

符号	编码	出现概率
A	0	0.2
B	10	0.2
C	110	0.3
D	111	0.3

在方法1中，平均每个符号的编码占用2个bits；在方法2中，平均每个符号的编码占用2.4个编码。其他的编码方式也许需要更多或更少的信息量来进行编码。

Entropy（熵）

那么，平均对每个符号进行编码的信息量的最小值是多少呢？这与每个字符在系统中的概率分布有关。

假设系统中有N个符号，符号$x_{i}$出现的概率为$p_{i}$，那么对该系统中每个符号进行编码平均所需的信息量（bits的数量）为:

$$H(X) = - \sum_{i=1}^{N}{p_{i}log_{2}(p_{i})}$$

这里的H(X)就是变量X的熵（entropy）。

Conditional Entropy（条件熵）

假设数据集有2个attribute，分别是X和Y，例如：

X	Y
Math	Yes
History	No
CS	Yes
Math	No
Math	No
CS	Yes
History	No
Math	Yes

那么，可以算出，
H(X) = 1.5， H(Y)=1。
H(Y|X=Math) = 1，H(Y|X=History) = 0，H(Y|X=CS) = 0。

可见，随机变量分布得越均匀，它的熵就越小。

条件熵H(Y|X)的算法为：

$$H(Y|X) = \sum_{j}{Pr(X=x_{j})·H(Y|X=x_{j})}$$

Infogamtion Gain

$$IG(Y|X) = H(Y) - H(Y|X)$$

信息增益的值总是非负的。

决策树算法

---

基本

决策树算法是一个贪心算法Greedy Algorithm，常常用于分类与回归。Tree ensemble algorithms（例如 random forests 和 boosting）常常是用于解决分类与回归问题的最好算法。

重点

决策树算法是一个supervised learning，因为训练集会提供每一个tuple的class tag。

决策树很容易理解，不多赘述了。其中，最关键的步骤是怎样选择一个最重要的attribute，并根据它的值来对数据集进行切分。

所谓最重要的attribute，是指用该attribute来切分数据集时，能够使得由数据集切分出的子集尽可能的纯净。

例如，如果按照某个attribute能将数据集切分成n个子集，且每个子集中的tuples都属于各自的class，那么，这个attribue就可以认为是最重要的attribute。因为这些切分出的子集，都是纯净的（**pure**）子集。

或者可以这样表述：最重要的attribute，是指用该attribute来切分数据集的前后，information gain最大

那么，怎样来选择最重要的attribute呢？有三种方法：
1. Information Gain (ID3算法使用)
2. Gain Ration (C4.5算法使用)
3. Gini Index (CART算法使用)

Attribute Selection Measures

---

构造决策树时，在每一个节点处，需要决定该节点选择哪一个attribute来对相应的数据集进行划分。理论上最好的attribute，将使得划分出的每一个子集中的数据都属于同一个class(这样的子集被称为pure partition)。当然实际上不大可能每一个节点都做到如此。

将训练数据集记为$D$，含有$m$个class，其中第$i$个class的子集记为$C_{i, D}$。

数据集的Entropy

Entropy被用于描述一个集合中的内容的不纯净程度（impurity），它在数学上的定义为：

$$Info(D) = - \sum_{i=1}^{m}{p_i log_2({p_i})}$$
这里，D为全集，共包含m个不同的class，$p_{i}$为D中第i个class所占的比例，即 $$p_{i} = \frac{|C_{i}|}{|D|}$$

D的entropy越高，它所包含的信息量越大。

如果D中的数据全部属于同一个class，那么D的entropy为0，显然这对于数据挖掘没什么用；如果D中有50%数据属于class A，50%数据属于class B，那么D的entropy为1，对于数据挖掘而言这是一个非常好的数据集。

在构造决策树时，我们希望知道：决定D中数据点属于哪一个class时，哪一个attribute是最重要的？ 而Information Gain就可以告诉我们哪一个attribute是最重要的。

Information Gain (信息增益)

关于Information Gain的概念， 这篇文档 讲的不错。

ID3算法采用了信息增益来选择最重要的attribute。

对于决策树中的dataset而言，它的信息增益为：

$$IG = entropyBeforeSplit - entropyAfterSplit$$
这里的entropyAfterSplit是决策树中某节点的所有branch中数据的entropy的带权之和，一个branch的权重就是该branch中的tuples数量与该节点中tuples数量之比。

如果将数据集按照attribute A进行划分，同时A在数据集中有v个值，并且按照A的属性值可以将D划分为对应的v个partition，即 $D_{1}$, $D_{2}$, ..., $D_{v}$，其中$D_{j}$中数据点的属性A的值为$v_{j}$。那么，数据集D在属性A处的entropy为：

$$Info_{A}{(D)} = \sum_{j=1}^{v} \frac{|D_{j}|}{|D|} \times Info(D_{j})$$
数据集D在属性A处的信息增益为：
$$IG_{A}{(D)} = Info(D) - Info_{A}{(D)}$$

对数据集的每一个attribute都计算其信息增益，选择信息增益最大的attribute来切分数据集。

举个例子：

Building the Decision Tree

---

构造决策树的过程是一个递归的过程。

1. 首先，选择数据集内信息增益最大的attribute作为根节点；
2. 为根节点的attribute的每种value分别创建一个branch，将对应的tuple归入该branch内。对每个branch内的数据子集，继续构造决策树。
3. 重复以上步骤, 直到某一个branche满足以下任意条件时停止：
   a). 所有的attribue都被用过了，如果此时该branch内的tuples不属于同一个class，则采用多数人投票的方法，为该branch添加一个leaf node，并为其标记一个class tag；
   b). 该branch内的所有数据点都属于同一个class，此时为该节点创建一个leaf node，并将其标记一个class tag；

Python代码实现

---

下面用Python代码来实现决策树的构造过程。为了简单起见，这里只支持nominal类型的数据。
假如我们有以下数据，来判断一个tuple是不是一条鱼：

Can survive without coming to surface?	Hash flippers?	Is it a fish?
1	1	yes
1	1	yes
1	0	no
0	1	no
0	1	no

这里，前两列是数据集的两种feature，最后一列是对应的class。
在下面的代码中，我们将假设数据集都是这种形式的。

创建数据集

def createDataset():
    dataset = [
        [1, 1, 'yes'],
        [1, 1, 'yes'],
        [1, 0, 'no'],
        [0, 1, 'no'],
        [0, 1, 'no']
    ]
    labels = ["Can Survive", "Has Flipper"]
    return dataset, labels

计算entropy

首先回忆一下怎样计算一个数据集D的entropy。

Entropy被用于描述一个集合中的内容的不纯净程度（impurity），它在数学上的定义为：

$$Info(D) = - \sum_{i=1}^{m}{p_i log_2({p_i})}$$
这里，D为全集，共包含m个不同的class，$p_{i}$为D中第i个class所占的比例，即 $$p_{i} = \frac{|C_{i}|}{|D|}$$

下面是实现代码。

def calcShannonEntropy(dataset):
    classCount = {}  # 每一种class的数量
    datasetSize = len(dataset)
    # 计算每一种class的在数据集中出现的次数
    for t in dataset:
        classTag = t[-1]
        if classTag not in classCount.keys():
            classCount[classTag] = 0
        classCount[classTag] += 1
    # 计算entropy
    entropy = 0.0
    for classTag in classCount.keys():
        prob = classCount[classTag]/float(datasetSize)
        entropy -= prob*log(prob, 2)
    return entropy

按照feature对数据集进行划分

############################################################
# 对数据集按照某个feature进行切分
# 其中，dataset的每个元素是一个一维数组(长度为N)，前N-1个元素每个
# 都是1个feature，最后一个元素是该数据的class tag。
# 本方法要按照第`splitIndex`个feature对数据集进行切分，
# 返回该feature的值等于`value`的所有记录
# splitIndex的范围在[0, N-1]之间：
# 返回的子集中，已经删除了splitIndex对应的feature，即返回的子集
# 中的每条记录含有N-2个feature
############################################################
def splitDataset(dataset, splitIndex, value):
    subset = []
    for t in dataset:
        if t[splitIndex] == value:
            reducedVec = t[:splitIndex]
            reducedVec.extend(t[splitIndex+1:])
            subset.append(reducedVec)
    return subset

请注意Python中List的两个方法（extend和append）的区别。

计算最重要的feature

回顾一下什么才算是最重要的feature。

如果将数据集按照attribute A进行划分，同时A在数据集中有v个不同的值，并且按照A的属性值可以将D划分为对应的v个partition，即 $D_{1}$, $D_{2}$, ..., $D_{v}$，其中$D_{j}$中数据点的属性A的值为$v_{j}$。那么，数据集D在属性A处的entropy为：

$$Info_{A}{(D)} = \sum_{j=1}^{v} \frac{|D_{j}|}{|D|} \times Info(D_{j})$$
数据集D在属性A处的信息增益为：
$$Info\_Gain_{A}{(D)} = Info(D) - Info_{A}{(D)}$$
对数据集的每一个attribute都计算其信息增益，信息增益最大的attribute就是最重要的feature（最能帮助划分数据）。

代码实现如下。

############################################################
# 对于包含N-1个feature的数据集，从中找出信息增益最大的feature，来
# 作为该数据集的splitting criteria
# 返回的是最重要的feature在数据集的每条tuple中的索引
############################################################
def chooseBestSplitCriteria(dataset):
    datasetSize = len(dataset)
    baseEntropy = calcShannonEntropy(dataset) # 数据集D的熵
    featNum = len(dataset[0])-1 # feature的数量（维度）
    bestCriteria = -1 # 最佳split属性的index
    maxInfoGain = 0.0 # 这里有个前提：info gain总是不小于0的！！
    for i in range(featNum): # 针对每一维的feature来计算
        featureValues = [t[i] for t in dataset]
        distinctFeatValues = set(featureValues)
        subEntropy = 0.0    # D在每一个属性处的entropy
        for v in distinctFeatValues: # 针对该feature的每一种值来计算
            subset = splitDataset(dataset, i, v)
            prob = len(subset)/float(datasetSize)
            subEntropy += prob * calcShannonEntropy(subset)
        # 调试用： 
        print "attribute index -> ", i, "\t subEntropy -> ", subEntropy, 
        "\t info gain -> ", baseEntropy - subEntropy
        if baseEntropy - subEntropy > maxInfoGain: # 寻找最大的信息增益
            maxInfoGain = baseEntropy - subEntropy
            bestCriteria = i
    return bestCriteria

构建Decision Tree

这里，我们用Josn的格式来表征一棵树，即：

{  root : {
        child1: { ... },
        child2: { ... },
        ...
        childN : { ... }
   }
}

回顾构造决策树的过程。

构造决策树的过程是一个递归的过程。

1. 首先，选择数据集内信息增益最大的attribute作为根节点；
2. 为根节点的attribute的每种value分别创建一个branch，将对应的tuple归入该branch内。对每个branch内的数据子集，继续构造决策树。
3. 重复以上步骤, 直到某一个branche满足以下任意条件时停止：
   a). 所有的attribue都被用过了，如果此时该branch内的tuples不属于同一个class，则采用多数人投票的方法，为该branch添加一个leaf node，并为其标记一个class tag；
   b). 该branch内的所有数据点都属于同一个class，此时为该节点创建一个leaf node，并将其标记一个class tag；
   
   

实现代码如下：

############################################################
# 为一个数据集(nominal类型)构建一颗decision tree
# attrLabels是所有attribues label的列表，其中的label的顺序
# 与dataeset中每个tuple中的attribute value的顺序必须是一致的
############################################################
def createDecisionTree(dataset, featLabels):
    classValueList = [t[-1] for t in dataset]  # 取出全部的class values
    # 如果dataset中全部的数据都属于同一个class，则返回该class
    if classValueList.count(classValueList[0]) == len(classValueList):
        return classValueList[0]
    # 如果dataset中已经没有attribute了，则返回所有class中的majority
    if (len(dataset[0]) == 1):
        return majorClass(classValueList)
    # 找出目前dataset中最重要的feature的index
    bestFeatIdx = chooseBestSplitCriteria(dataset)
    bestFeatLabel = featLabels[bestFeatIdx]
    subFeatLabels = featLabels[:]
    del(subFeatLabels[bestFeatIdx])  # 去掉已经用过的feature label
    tree = { bestFeatLabel:{ } } # 构造根节点
    # 下面处理根节点的每一个branch
    featValueSet = set([t[bestFeatIdx] for t in dataset])
    for featValue in featValueSet:
        tree[bestFeatLabel][featValue] = createDecisionTree(
            splitDataset(dataset, bestFeatIdx, featValue),
            subFeatLabels)
    return tree
############################################################
# 找出最主流的class(按照频率计算)
############################################################
def majorClass(classList):
    classCountMap = {}
    for clz in classList:
        if clz not in classCountMap.keys():
            classCountMap[clz] = 1
        else:
            classCountMap[clz] += 1
    # 按照value进行排序，并返回频次最高的class的tag
    return sorted(classCountMap.iteritems(), key=operator.itemgetter(1), reverse=True)[0][3]

测试数据验证

---

例1

我们要本文上面提到的数据集来验证。

数据集如下：

Can survive without coming to surface?	Hash flippers?	Is it a fish?
1	1	yes
1	1	yes
1	0	no
0	1	no
0	1	no

创建数据集的代码为

def createDataset():
    dataset = [
        [1, 1, 'yes'],
        [1, 1, 'yes'],
        [1, 0, 'no'],
        [0, 1, 'no'],
        [0, 1, 'no']
    ]
    labels = ["Can Survive", "Has Flipper"]
    return dataset, labels

调用createDecisionTree方法

dataset, labels = createDataset()
print json.dumps(createDecisionTree(dataset, labels), indent=4)

输出结果如下：

{
    "Survive": {
        "0": "no", 
        "1": {
            "Fish": {
                "0": "no", 
                "1": "yes"
            }
        }
    }
}

例2

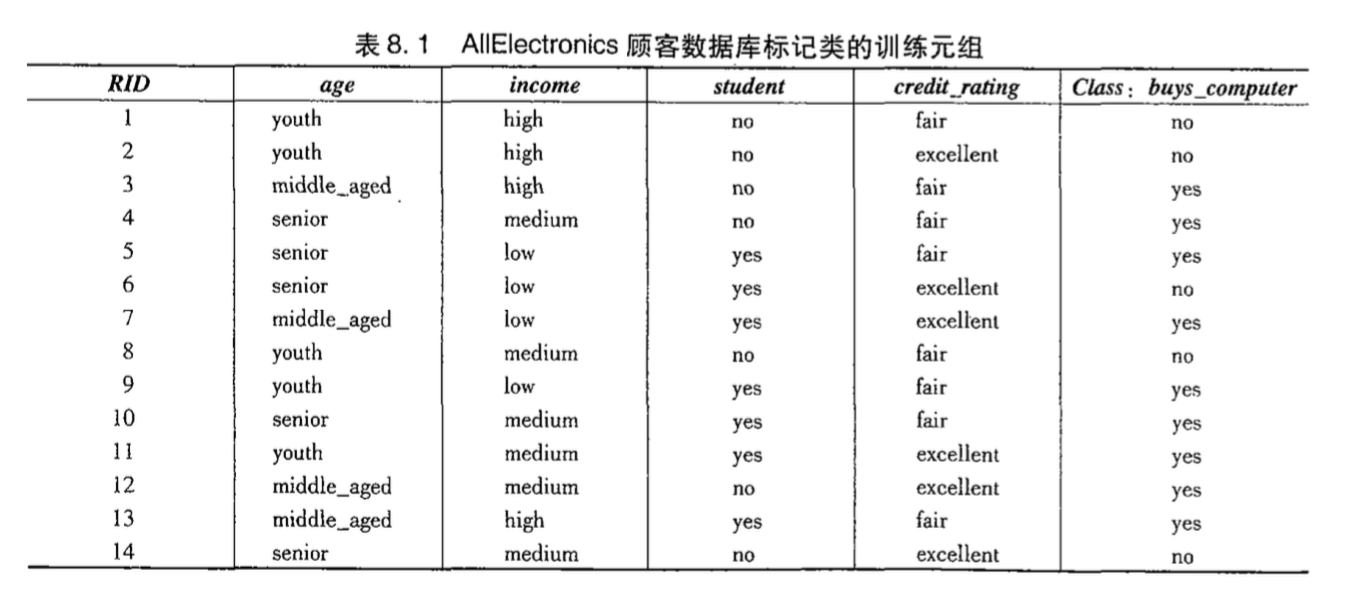
我们再用《Data Mining: Concepts and Techniques》中的例子来测试。

数据集如下:

创建数据集：

############################################################
# 再用一组新数据来测试
# 数据来源：《Data Mining: Concepts and Techniques》
############################################################
def generateDataSet():
    dataset = [
        ['youth',       'high',     'no',   'fair',         'no'],
        ['youth',       'high',     'no',   'excellent',    'no'],
        ['middle_aged', 'high',     'no',   'fair',         'yes'],
        ['senior',      'medium',   'no',   'fair',         'yes'],
        ['senior',      'low',      'yes',  'fair',         'yes'],
        ['senior',      'low',      'yes',  'excellent',    'no'],
        ['middle_aged', 'low',      'yes',  'excellent',    'yes'],
        ['youth',       'medium',   'no',   'fair',         'no'],
        ['youth',       'low',      'yes',  'fair',         'yes'],
        ['senior',      'medium',   'yes',  'fair',         'yes'],
        ['youth',       'medium',   'yes',  'excellent',    'yes'],
        ['middle_aged', 'medium',   'no',   'excellent',    'yes'],
        ['middle_aged', 'high',     'yes',  'fair',         'yes'],
        ['senior',      'medium',   'no',   'excellent',    'no']
    ]
    labels = ['age', 'income', 'student', 'credit_rating', 'buys_computer']
    return dataset, labels

调用createDecisionTree方法

dataset, labels = generateDataSet()
print json.dumps(createDecisionTree(dataset, labels), indent=4)

输出结果为：

{
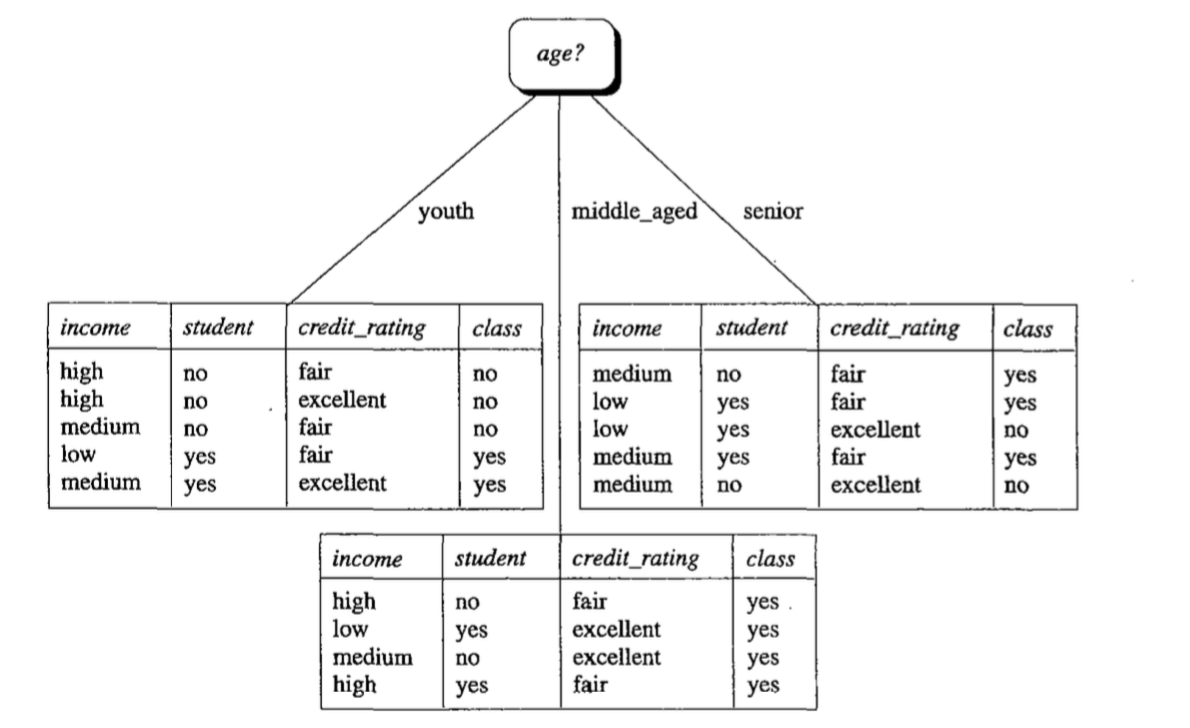
    "age": {
        "youth": {
            "student": {
                "yes": "yes", 
                "no": "no"
            }
        }, 
        "senior": {
            "credit_rating": {
                "fair": "yes", 
                "excellent": "no"
            }
        }, 
        "middle_aged": "yes"
    }
}

这与书上构造出的决策树是一样的。

使用决策树来预测分类

---

上面已经构建出了决策树，下面将用构建出的决策树预测输入数据的分类情况。

###################################################################
# tree ： 构建出的决策树
# featLabels : feature的名字的列表，例如 ["Survive", "Fish"]
# testVec：一条测试数据，但是不知道其class
###################################################################
def classify(tree, featLabels, testVec):
    firstStr = tree.keys()[0]
    innerDict = tree[firstStr]
    featIndex = featLabels.index(firstStr)
    for key in innerDict.keys() :
        if key == testVec[featIndex]:
            if type(innerDict[key]).__name__ == 'dict':
                return classify(innerDict[key], featLabels, testVec)
            else:
                return innerDict[key]
# 测试新的数据的预测分类
dataset, labels = createDataset()
decisionTree = createDecisionTree(dataset, labels)
# print decisionTree
print classify(decisionTree, ["Survive", "Fish"], [1, 0])
dataset, labels = trees.generateDataSet()
decisionTree = trees.createDecisionTree(dataset, labels)
print classify(decisionTree, ['age', 'income', 'student', 'credit_rating'], ['senior',      'medium',   'no',   'excellent'])

使用MLLib中的决策树工具

---

参考：
+

Spark版本：CDH5.4.7 - Spark 1.3

我们对上面例1和例2中的数据，应用MLLib来构建决策树。

package cn.gridx.spark.examples.MLlib.algo
import org.apache.log4j.{Level, Logger}
import org.apache.spark.{SparkConf, SparkContext}
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.mllib.tree.DecisionTree
import org.apache.spark.mllib.tree.model.DecisionTreeModel
/**
 * Created by tao on 11/30/15.
 *
 *  对MLlib中的决策树工具的使用例子(Spark 1.3)
 *
 *  参考：   http://web.cs.ucla.edu/~linmanna/cs239/
 *          https://spark.apache.org/docs/1.3.0/mllib-decision-tree.html
 *          https://databricks.com/blog/2014/09/29/scalable-decision-trees-in-mllib.html
 *
 */
object DecisionTreesExample {
    def main(args: Array[String]): Unit = {
        Logger.getRootLogger.setLevel(Level.ERROR)
        val sc = new SparkContext(new SparkConf())
        Test_SmallCategoricalDataset_1(sc)
        println("\n\n\n")
        Test_SmallCategoricalDataset_2(sc)
        sc.stop
    }
    /** 用一个小数据集来测试决策树
     * 数据集中的tuple的全部feature都是categorical
     * dataset = [
                [1, 1, 'yes'],
                [1, 1, 'yes'],
                [1, 0, 'no'],
                [0, 1, 'no'],
                [0, 1, 'no']
            ]
            'yes'记为1, 'no'记为1
     */
    def Test_SmallCategoricalDataset_1(sc: SparkContext): Unit = {
        val trainingData = sc.parallelize(Array(
            LabeledPoint(1, Vectors.dense(1, 1)),
            LabeledPoint(1, Vectors.dense(1, 1)),
            LabeledPoint(0, Vectors.dense(1, 0)),
            LabeledPoint(0, Vectors.dense(0, 1)),
            LabeledPoint(0, Vectors.dense(0, 1))))
        val numClasses = 2
        // categorical feature info，为空则认为所有的feature都是连续性变量
        val categoricalFeatureInfo = Map(0 -> 2, 1 -> 2) 
        val impurity = "entropy" // 或者是gini
        val maxDepth = 5
        val maxBins = 32
        val model: DecisionTreeModel = 
            DecisionTree.trainClassifier(trainingData, numClasses,
                categoricalFeatureInfo, impurity, maxDepth, maxBins)
        // 将训练出的模型持久化到HDFS文件中，然后再将其读出来使用
        def modelPath = "/user/tao/mllib/model/tree.model"
        model.save(sc, modelPath)
        val sameModel = DecisionTreeModel.load(sc, modelPath)
        /**
         * 输出
         * DecisionTreeModel classifier of depth 2 with 5 nodes
              If (feature 0 in {0.0})
               Predict: 0.0
              Else (feature 0 not in {0.0})
               If (feature 1 in {0.0})
                Predict: 0.0
               Else (feature 1 not in {0.0})
                Predict: 1.0
            这与例1中的结果是一样的！
         */
        println("="*30 + " full model in the form of a string " + "="*30)
        println(sameModel.toDebugString)
        println("="*30 + " testing prediction " + "="*30)
        println("(1, 1) -> " + sameModel.predict(Vectors.dense(1,1)))
        println("(0, 1) -> " + sameModel.predict(Vectors.dense(0,1)))
    }
    /**
     * 另一个数据集，来自 Data Mining: Concepts and Techniques, 3rd edition
      是上面例2中的数据集
     * @param sc
     */
    def Test_SmallCategoricalDataset_2(sc: SparkContext): Unit = {
        val originalDataset = Array(
                ("youth",       "high",     "no",   "fair",         "no"),
                ("youth",       "high",     "no",   "excellent",    "no"),
                ("middle_aged", "high",     "no",   "fair",         "yes"),
                ("senior",      "medium",   "no",   "fair",         "yes"),
                ("senior",      "low",      "yes",  "fair",         "yes"),
                ("senior",      "low",      "yes",  "excellent",    "no"),
                ("middle_aged", "low",      "yes",  "excellent",    "yes"),
                ("youth",       "medium",   "no",   "fair",         "no"),
                ("youth",       "low",      "yes",  "fair",         "yes"),
                ("senior",      "medium",   "yes",  "fair",         "yes"),
                ("youth",       "medium",   "yes",  "excellent",    "yes"),
                ("middle_aged", "medium",   "no",   "excellent",    "yes"),
                ("middle_aged", "high",     "yes",  "fair",         "yes"),
                ("senior",      "medium",   "no",   "excellent",    "no"))
        // 对数据集进行转换
        val dataSet: Array[LabeledPoint]
            = originalDataset.map(t => LabeledPoint(
                t._5 match {    // class tag
                    case "no"  => 0
                    case "yes" => 1
                },
                Vectors.dense(  // features
                    t._1 match {
                        case "youth"       => 0
                        case "middle_aged" => 1
                        case "senior"      => 2
                    },
                    t._2 match {
                        case "high"   => 0
                        case "medium" => 1
                        case "low"    => 2
                    },
                    t._3 match {
                        case "no"  => 0
                        case "yes" => 1
                    },
                    t._4 match {
                        case "excellent" => 0
                        case "fair"      => 1
                    })))
        println("="*30 + " dataset " + "="*30)
        dataSet.foreach(println)
        val trainingData = sc.parallelize(dataSet)
        val numClasses = 2
        val categoricalFeatureInfo: Map[Int, Int] = Map(0 -> 3, 1 -> 3, 2 -> 2, 3 -> 2)
        val impurity = "entropy"
        val maxDepth = 20
        val maxBin = 32
        val model = 
            DecisionTree.trainClassifier(trainingData, numClasses, 
                categoricalFeatureInfo, impurity, maxDepth, maxBin)
        /**
         * DecisionTreeModel classifier of depth 4 with 13 nodes
              If (feature 2 in {0.0})
               If (feature 0 in {0.0})
                Predict: 0.0
               Else (feature 0 not in {0.0})
                If (feature 0 in {2.0})
                 If (feature 3 in {0.0})
                  Predict: 0.0
                 Else (feature 3 not in {0.0})
                  Predict: 1.0
                Else (feature 0 not in {2.0})
                 Predict: 1.0
              Else (feature 2 not in {0.0})
               If (feature 0 in {0.0,1.0})
                Predict: 1.0
               Else (feature 0 not in {0.0,1.0})
                If (feature 3 in {0.0})
                 Predict: 0.0
                Else (feature 3 not in {0.0})
                 Predict: 1.0
            但是，这与书上的例子计算出的Model的结构不同！！！
         */
        println("="*30 + " full model in the form of a string " + "="*30)
        println(model.toDebugString)
        println("="*30 + " testing prediction " + "="*30)
        println("(2, 1, 0, 0) -> " + model.predict(Vectors.dense(2, 1, 0, 0)))
    }
}