降低一个八度：使用八度卷积减少卷积神经网络的空间冗余

刘源

---

论文地址：Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution

摘要

在自然图像中，信息总是在不同频率中表达的，其中高频信号一般包含丰富的细节而低频信号一般包含整体的结构。类似地，卷积层的输出特征图同样可以被看作是混合了不同频域的信息。在这项工作中，我们提出了如何根据频域去分解信息混合的特征图，并设计了一个新颖的八度卷积（Octave Convolution，OctConv）操作来保存和处理那些在较低空间分辨率下变化“较慢”（Slower）的特征图，从而减少存储和计算开销。与现有多尺度（multi-scale）方法不同的是，八度卷积被制定为一种单个通用的即插即用卷积单元，可以直接替换普通（vanilla）卷积而不需要对现有网络有任何调整。它同时也是对一些表明有着更好拓扑（topologies）或者减少通道冗余的方法的补充，并且与这些方法正交（orthogonal）。通过简单地用八度卷积替换普通卷积，我们在实验中发现我们在减少存储和计算开销的同时，还能持续提高图像和视频识别任务的准确率。一个使用八度卷积的ResNet-152网络能够在ImageNet上达到82.9%的Top-1分类准确率，而其浮点计算量仅仅只有22.2G（Giga）。

为什么要分离不同频域的信息？

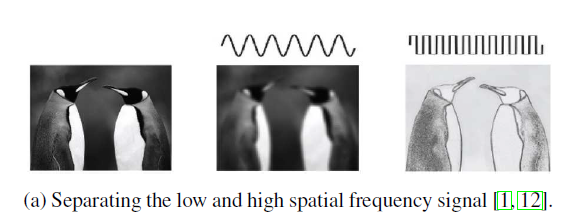
图-1 分离低和高空间频率信号
在传统的图像处理中，我们发现自然图像里，高频信号描述的是剧烈变化的丰富细节（如图-1中的第三幅图），而低频信号描述的是平缓变化的整体结构，如轮廓（图-1中的第二幅图）。作者等人认为，在卷积神经网络中，卷积层的输出同样混合着这两种信号。

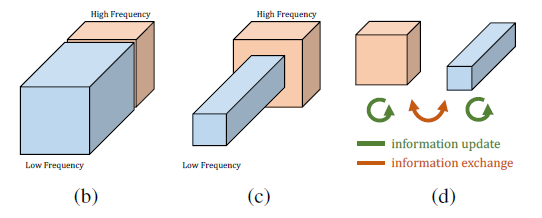
图-2 卷积层的输出混合着低频和高频信号
对于低频信号，我们可以通过共享邻接位置的信息来降低空间冗余（如图-2(c)所示）。因此，从卷积层的输出特征图中分离出包含低频信息的特征图，让我们能够对其进行下采样处理，从而减少空间冗余。为了让卷积层适应这种新特征图表达方式，作者在普通卷积的基础上提出了八度卷积，让特征图在卷积的过程中，低频和高频特征图能完成自身信息更新的同时，还能在彼此之间完成信息交换，从而实现普通卷积的信息提取效果。

八度特征表示与八度卷积

对于普通卷积而言，所有输入和输出特征图的通道都有着一样的分辨率。而作者这里提出的八度特征表示中，低频特征图的分辨率仅有高频特征图的一半（如图-3所示）。在八度特征表示的基础上，作者提出了八度卷积方式来替换普通卷积。

普通卷积

普通卷积的卷积公式如下：

$$Y_{p,q}=\sum_{i,j\in\mathcal{N}_k}W_{i+\frac{k-1}{2},j+\frac{k-1}{2}}^TX_{p+i,q+j}$$
其中$p,q$表示位置坐标而$\mathcal{N}_k=\{(i,j):i=\{-\frac{k-1}{2},\cdots,\frac{k-1}{2}\},j=\{-\frac{k-1}{2},\cdots,\frac{k-1}{2}\}\}$表示局部的邻接集合。为了简单起见，作者这里不考虑填充（padding），并且假设$k$是奇数以及输入输出通道数一样$c_{in}=c_{out}=c$。

八度卷积

设八度卷积的输入输出分别为$X,Y$，那么$X$由八度特征表示可知分别为$\{X^{L},X^H\}$，而$Y=\{Y^H,Y^L\}$。$Y^{A\rightarrow B}$表示从特征图组$A$到$B$的卷积更新过程，那么$Y^H=Y^{H\rightarrow H}+Y^{L\rightarrow H}$和$Y^L=Y^{H\rightarrow L}+Y^{L\rightarrow L}$。特别地，$Y^{H\rightarrow H},Y^{L\rightarrow L}$表示频率内信息更新，而$Y^{L\rightarrow H},Y^{H\rightarrow L}$表示频率间信息交流。
而为了完成这些卷积计算，作者将普通卷积地卷积核$W$分裂成两个部分$[W^H,W^L]$，分别用于卷积$X^H,X^L$。每个部分又可以进一步分为频率内和频率间两个部分：$W^H=[W^{H\rightarrow H},W^{L\rightarrow L}]$和$W^L=[W^{L\rightarrow L},W^{H\rightarrow L}]$，如图-4所示。
为了控制输入和输出特征图的低频信息部分的比例，作者引入了超参数$\alpha_{in}$和$\alpha_{out}$，一般而言，$\alpha_{in}=\alpha_{out}$。
对于高频特征图，它的频率内信息更新过程就是普通卷积过程，而频率间的信息交流过程，则可以对$X^L$使用上采样操作然后再进行卷积。类似地，对于低频特征图，它的频率内信息更新过程就是普通卷积过程，而频率间的信息交流过程则通过对$X^H$进行平均池化操作然后再进行卷积实现。更新过程如图-3所示。

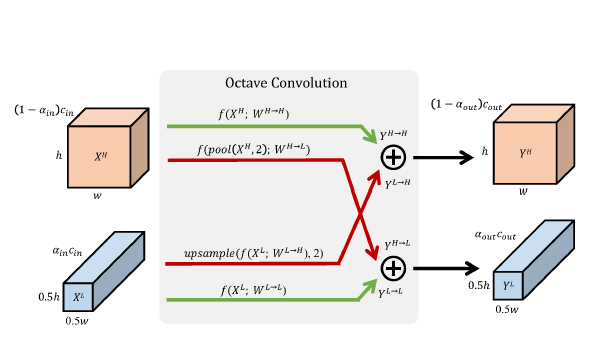
图-3 八度特征表示与八度卷积过程

图-4 分裂卷积核用于八度卷积
对于八度卷积而言，最有意思和有用的属性就是由于低频特征图的分辨率变小，实际上八度卷积的感受野反而变大了，所以在使用$k\times k$卷积核去卷积低频特征图$X^L$情况下，八度卷积有着几乎等价于2倍普通卷积感受野的能力，着进一步帮助八度卷积层捕捉远距离的上下文信息从而潜在地提升识别性能。
需要注意的是，第一层和最后一层八度卷积层的超参数$\alpha$应当分别设为$\alpha_{in}=0,\alpha_{out}=\alpha$和$\alpha_{in}=\alpha,\alpha_{out}=0$，如图-5和图-6。而中间的八度卷积层则一般设为$\alpha_{in}=\alpha_{out}=\alpha$。如此一来，即可完成即插即用的替换。

图-5 第一层八度卷积的输入是常规的

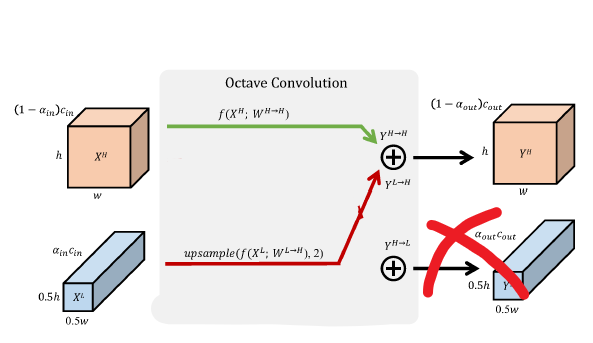
图-6 最后一层八度卷积的输出是常规的

使用平均池化而不是步长为2的卷积进行下采样

在八度卷积中，高频特征图卷积需要经过下采样，随后才能卷积到低频特征图。在这里作者讨论了下采样方式的选择。一般而言，在深度神经网络中，下采样有池化和步长为2的卷积这两种主要的下采样方式。在这里，作者发现了，使用步长为2的卷积之后（高频到低频），再经过上采样（低频到高频）会导致出现中心偏移的错位情况（misalignment），如图-7所示。出现错位的情况后如果还是照常加上其他特征图，那么就会出现问题。

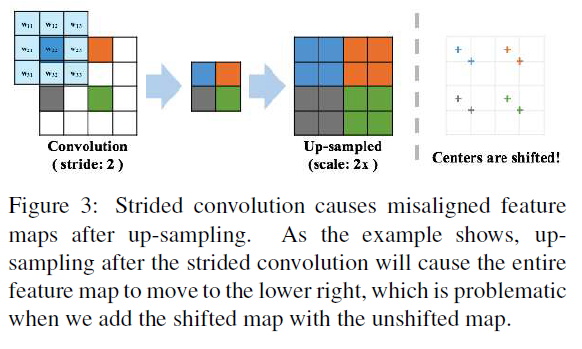
图-7 特征图经过步长为2的卷积后，再经过上采样（如最近邻插值），会导致错位的情况
随后作者在实验中对比了这两种下采样方式以及信息交换的影响，如表

表-1 步长为2的卷积与平均池化，高频到低频与低频到高频信息交换的两组对照实验

实验结果

表-2 八度卷积在不同$\alpha$下的计算和存储开销
作者首先测量了不同超参$\alpha$下，八度卷积带来的计算和存储开销减少，如表-1所示。

图-8 八度卷积在ImageNet上的消融研究，横轴是浮点计算量，纵轴是Top-1准确率
随后作者在ImageNet上进行了消融研究。实验结果表明，使用了八度卷积的网络浮点计算量更少，准确率更高。

表-3 ResNet-50使用普通卷积和八度卷积在CPU上推理时间的对比

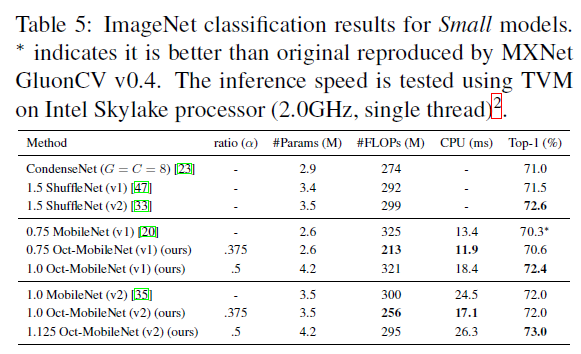
表-4 八度卷积在小模型上的ImageNet实验结果与对比

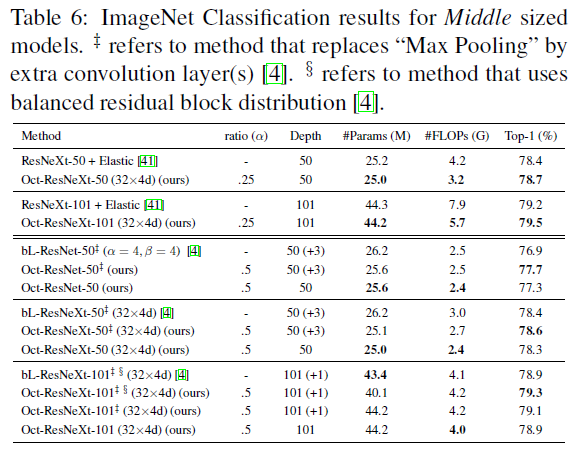
表-5 八度卷积在中等模型上的ImageNet实验结果与对比

表-6 八度卷积在大模型上的ImageNet实验结果与对比

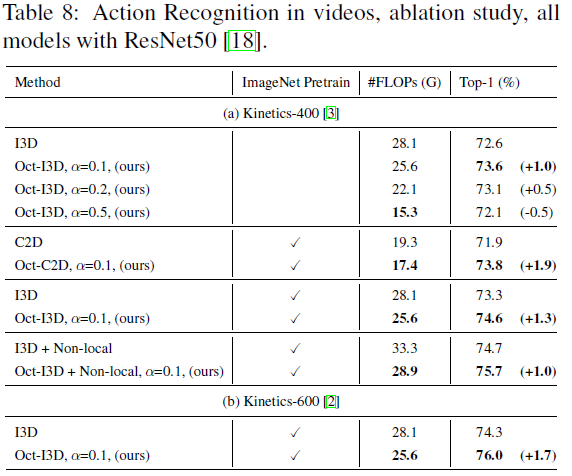
表-7 八度卷积在行为识别上的实验结果与对比
作者除了在分类任务上做了大量的实验和对比，还在行为识别这类目标检测任务上进行了实验和对比。

类似的思想

八度卷积的核心思想其实和这篇类小波变换自动编码器差不多Learning a Wavelet-like Auto-Encoder to Accelerate Deep Neural Networks，都是通过降低空间分辨率来达到存储和计算开销的减少。

简单的PyTorch实现（仅供参考）

笔者给出了一个简单的八度卷积实现，希望读者们能够多多批评指正。

import math
import torch
import torch.nn as nn
import torch.nn.functional as F
class OctConv2d(nn.Conv2d):
    def __init__(
        self,
        in_channels,
        out_channels,
        kernel_size,
        stride=1,
        padding=0,
        dilation=1,
        groups=1,
        bias=True,
        alpha_in=0.5,
        alpha_out=0.5,):
        assert alpha_in >= 0 and alpha_in <= 1
        assert alpha_out >= 0 and alpha_out <= 1
        super(OctConv2d, self).__init__(in_channels, out_channels,
                                        kernel_size, stride, padding,
                                        dilation, groups, bias)
        self.avgpool = nn.AvgPool2d(kernel_size=2, stride=2)
        self.alpha_in = alpha_in
        self.alpha_out = alpha_out
        self.inChannelSplitIndex = math.floor(
            self.alpha_in * self.in_channels)
        self.outChannelSplitIndex = math.floor(
            self.alpha_out * self.out_channels)

    def forward(self, input):
        if not isinstance(input, tuple):
            assert self.alpha_in == 0 or self.alpha_in == 1
            inputLow = input if self.alpha_in == 1 else None
            inputHigh = input if self.alpha_in == 0 else None
        else:
            inputLow = input[0]
            inputHigh = input[1]


        output = [0, 0]
        # H->H
        if self.outChannelSplitIndex != self.out_channels and self.inChannelSplitIndex != self.in_channels:
            outputH2H = F.conv2d(
                inputHigh,
                self.weight[
                    self.outChannelSplitIndex:,
                    self.inChannelSplitIndex:,
                    :,
                    :],
                self.bias[
                    self.outChannelSplitIndex:],
                self.stride,
                self.padding,
                self.dilation,
                self.groups)
            output[1] += outputH2H

        # H->L
        if self.outChannelSplitIndex != 0 and self.inChannelSplitIndex != self.in_channels:
            outputH2L = F.conv2d(
                self.avgpool(inputHigh),
                self.weight[
                    :self.outChannelSplitIndex,
                    self.inChannelSplitIndex:,
                    :,
                    :],
                self.bias[
                    :self.outChannelSplitIndex],
                self.stride,
                self.padding,
                self.dilation,
                self.groups)
            output[0] += outputH2L

        # L->L
        if self.outChannelSplitIndex != 0 and self.inChannelSplitIndex != 0:
            outputL2L = F.conv2d(
                inputLow,
                self.weight[
                    :self.outChannelSplitIndex,
                    :self.inChannelSplitIndex,
                    :,
                    :],
                self.bias[
                    :self.outChannelSplitIndex],
                self.stride,
                self.padding,
                self.dilation,
                self.groups)
            output[0] += outputL2L

        # L->H
        if self.outChannelSplitIndex != self.out_channels and self.inChannelSplitIndex != 0:
            outputL2H = F.conv2d(
                F.interpolate(inputLow, scale_factor=2),
                self.weight[
                    self.outChannelSplitIndex:,
                    :self.inChannelSplitIndex,
                    :,
                    :],
                self.bias[
                    self.outChannelSplitIndex:],
                self.stride,
                self.padding,
                self.dilation,
                self.groups)
            output[1] += outputL2H

        return tuple(output)