PyTorch入门：一个简单但强大的深度学习库

叶虎

本文翻译自An Introduction to PyTorch – A Simple yet Powerful Deep Learning Library，原作者保留版权。

引言

每过一段时间，一个新的深度学习Python库会被开发，它有可能对深度学习领域进行改观。PyTorch就是这样的一个深度学习库。最近几周，我开始接触PyTorch，我深深震惊于其是如此容易上手。在我目前所使用的各种各样的深度学习库中，PyTorch无疑是最灵活与容易学习的。

在这篇文章中，我们通过动手实践来介绍PyTorch，不仅包含PyTorch的基础知识，还有一个实战案例。文中会使用Numpy和PyTorch从零开始实现一个神经网络，通过对比可以看出它们的相似之处。
让我们开始吧！

注意：这里要求你对深度学习有一定的基础，如果你想快速入门深度学习，可以先看一下这篇文章。

目录

• PyTorch概述
• PyTorch基础
• 使用Numpy和PyTorch实现一个神经网络
• 与其它深度学习库的对比
• 实战-使用PyTorch解决一个图像识别问题

PyTorch概述

PyTorch的发明者们说他们的设计理念是命令式，这意味着可以立即运行计算。这契合Python的编程方式，我们不想等到实现所有代码后才能知道当前的代码是否有效，相反，我们可以非常容易运行一部分代码，并进行实时检查。对于神经网络模型的调试，这将是一个福音。

作为一个深度学习开发平台，PyTorch是一个基于Python的库，故具有很大灵活性。PyTorch的使用方式非常接近Python中最常用科学计算库Numpy。你可能会问，为什么要选择PyTorch来开发深度学习模块？这里列举了一些原因：

• 极简的API：和使用Python一样容易；
• 支持Python：像前面所说，PyTorch完美集成了Python的数据科学栈，使用它就和Numpy差不多；
• 动态计算图：PyTorch不是预先定义计算图，而是提供一个动态计算图，甚至在运行时可以改变它。当你不知道要为你的网络分配多大内存时，PyTorch就很有用。

PyTorch的另外优势是提供多GPU支持，而且提供规范的数据加载模块以及简单的预处理模块。

自从PyTorch在2016年1月份发布，越来越多的研究者开始使用它，这主要是因为它非常容易建立新奇的甚至是极其复杂的计算图。话所如此，由于PyTorch比较新而且在持续开发中，距离其被大部分数据科学家使用还需一段时间。

PyTorch基础

在讲解技术细节之前，我们先来认识一下PyTorch的工作方式。PyTorch采用imperative/eager范式，意思是建立计算图的每行代码定义了计算图的一部分。我们可以独立运行计算图的各个部分，甚至在整个计算图完全建立前。这称为“define-by-run” 方式。

来源: http://pytorch.org/about/

PyTorch的安装非常容易，你只需要按照官方文档说明在你的系统（目前不支持Windows）中运行特定的命令即可。下面是我所使用的命令：

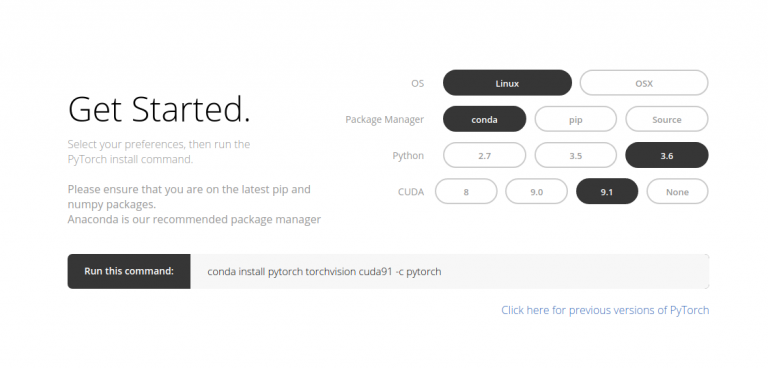
conda install pytorch torchvision cuda91 -c pytorch

入门PyTorch所需知道的基础知识包括：

• PyTorch张量
• 数学运算
• Autograd模块
• Optim模块
• nn模块

下面，我们逐个介绍它们。

PyTorch张量

张量（Tensors）就是多维数组而已。PyTorch的张量与Numpy中的ndarrays相似，但是支持在GPU运算。PyTorch支持各种各样的张量。你可以如下定义一个向量：

# import pytorch
import torch

# 定义一个向量
torch.FloatTensor([2])
# 输出
 2
[torch.FloatTensor of size 1]

数学运算

与Numpy一样，一个科学计算库必须支持高效的数学运算。PyTorch提供了与Numpy类似的接口，里面有200+的数学运算你可以使用。下面是一个PyTorch的加法实例：

a = torch.FloatTensor([2])
b = torch.FloatTensor([3])
a + b
# 输出
5
[torch.FloatTensor of size 1]

看起来和Python使用起来一样。我们还可以进行各种各样的矩阵运算，如下对一个矩阵进行转置：

matrix = torch.randn(3, 3)
matrix
-1.3531 -0.5394  0.8934
 1.7457 -0.6291 -0.0484
-1.3502 -0.6439 -1.5652
[torch.FloatTensor of size 3x3]

matrix.t()
-2.1139  1.8278  0.1976
 0.6236  0.3525  0.2660
-1.4604  0.8982  0.0428
[torch.FloatTensor of size 3x3]

Autograd模块

PyTorch在Autograd模块中提供了自动求导功能。要使用自动求导，你需要知道一个特殊的类Variable，其可以看成Tensor的包装器，因为你可以像使用Tensor一样对其进行数学运算。要得到Variable的Tensor，你可以通过data属性，另外Variable包含grad属性，其是梯度值。不同于Tensor，Variable可以记录其进行的数学运算（在grad_fn中），这样你可以通过反向过程计算其梯度值，这是基于链式法则进行求导，backward()函数用于实现反向运算，从而得到梯度值。对于构建神经网络，自动求导是非常有用的。

来源: http://pytorch.org/about/

import torch
from torch.autograd import Variable
x = Variable(torch.ones(2, 2), requires_grad=True)
x.data
 1  1
 1  1
 [torch.FloatTensor of size 2x2]

y = x + 2
z = y * y * 3
out = z.mean()
x.grad
 Variable containing:
 4.5000  4.5000
 4.5000  4.5000
 [torch.FloatTensor of size 2x2]

Optim模块

Optim模块主要实现了各种各样的优化算法，其用于训练神经网络。大部分的常用优化算法是支持的，因此你不必自己从零去实现。下面是定义一个Adam优化器：

optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

nn模块

基于Autograd模块你可以定义一个计算图并可以自动求梯度。但是原始的Autograd模块对于构建复杂的神经网络还是比较低级，这就需要使用nn模块了。nn包中定义了一系列子模块，其可以看成一个网络层，其包含一些可训练的参数，并能接受输入产生输出。你可以将nn模块看成PyTorch的Keras!

import torch

# 定义模型
model = torch.nn.Sequential(
 torch.nn.Linear(input_num_units, hidden_num_units),
 torch.nn.ReLU(),
 torch.nn.Linear(hidden_num_units, output_num_units),
)
loss_fn = torch.nn.CrossEntropyLoss()

现在你掌握了PyTorch的基础模块，那么就可以很容易地从零开始构建自己的网络模型。

使用Numpy和PyTorch实现一个神经网络

前面说过，PyTorch和Numpy是极其相似。这个部分，我们分别使用Numpy和PyTorch来实现一个简单的神经网络，来解决一个二分类问题（详情参考这里）
首先是使用Numpy的实现：

# Numpy实现神经网络

import numpy as np

# 输入
X=np.array([[1,0,1,0],[1,0,1,1],[0,1,0,1]])

# 输出
y=np.array([[1],[1],[0]])

# Sigmoid
def sigmoid (x):
 return 1/(1 + np.exp(-x))

# Sigmoid导数
def derivatives_sigmoid(x):
 return x * (1 - x)

# 参数设置
epoch=5000 #训练步长
lr=0.1 #学习速率
inputlayer_neurons = X.shape[1] #特征数
hiddenlayer_neurons = 3 #隐含层神经元数
output_neurons = 1 #输出维度

#权重初始化
wh=np.random.uniform(size=(inputlayer_neurons,hiddenlayer_neurons))
bh=np.random.uniform(size=(1,hiddenlayer_neurons))
wout=np.random.uniform(size=(hiddenlayer_neurons,output_neurons))
bout=np.random.uniform(size=(1,output_neurons))

for i in range(epoch):
  #前向过程
  hidden_layer_input1=np.dot(X,wh)
  hidden_layer_input=hidden_layer_input1 + bh
  hiddenlayer_activations = sigmoid(hidden_layer_input)
  output_layer_input1=np.dot(hiddenlayer_activations,wout)
  output_layer_input= output_layer_input1+ bout
  output = sigmoid(output_layer_input)

  #反向过程
  E = y-output
  slope_output_layer = derivatives_sigmoid(output)
  slope_hidden_layer = derivatives_sigmoid(hiddenlayer_activations)
  d_output = E * slope_output_layer
  Error_at_hidden_layer = d_output.dot(wout.T)
  d_hiddenlayer = Error_at_hidden_layer * slope_hidden_layer
  wout += hiddenlayer_activations.T.dot(d_output) *lr
  bout += np.sum(d_output, axis=0,keepdims=True) *lr
  wh += X.T.dot(d_hiddenlayer) *lr
  bh += np.sum(d_hiddenlayer, axis=0,keepdims=True) *lr

print('actual :\n', y, '\n')
print('predicted :\n', output)

下面尝试用PyTorch来实现这个网络，可以看到除了接口不一样外，其它的全部与Numpy一样：

## pytorch实现网络
import torch

#输入
X = torch.Tensor([[1,0,1,0],[1,0,1,1],[0,1,0,1]])

#输出
y = torch.Tensor([[1],[1],[0]])

#Sigmoid 
def sigmoid (x):
  return 1/(1 + torch.exp(-x))

#Sigmoid导数
def derivatives_sigmoid(x):
  return x * (1 - x)

#参数设置
epoch=5000 #训练步长
lr=0.1 #学习速率
inputlayer_neurons = X.shape[1] #输入维度
hiddenlayer_neurons = 3 #隐含层神经元数目
output_neurons = 1 #输出维度

#权重初始化
wh=torch.randn(inputlayer_neurons, hiddenlayer_neurons).type(torch.FloatTensor)
bh=torch.randn(1, hiddenlayer_neurons).type(torch.FloatTensor)
wout=torch.randn(hiddenlayer_neurons, output_neurons)
bout=torch.randn(1, output_neurons)

for i in range(epoch):

  #前向过程
  hidden_layer_input1 = torch.mm(X, wh)
  hidden_layer_input = hidden_layer_input1 + bh
  hidden_layer_activations = sigmoid(hidden_layer_input)

  output_layer_input1 = torch.mm(hidden_layer_activations, wout)
  output_layer_input = output_layer_input1 + bout
  output = sigmoid(output_layer_input1)

  #反向过程
  E = y-output
  slope_output_layer = derivatives_sigmoid(output)
  slope_hidden_layer = derivatives_sigmoid(hidden_layer_activations)
  d_output = E * slope_output_layer
  Error_at_hidden_layer = torch.mm(d_output, wout.t())
  d_hiddenlayer = Error_at_hidden_layer * slope_hidden_layer
  wout += torch.mm(hidden_layer_activations.t(), d_output) *lr
  bout += d_output.sum() *lr
  wh += torch.mm(X.t(), d_hiddenlayer) *lr
  bh += d_output.sum() *lr

print('actual :\n', y, '\n')
print('predicted :\n', output)

尽管如此，一般情况下我们会倾向于使用nn高级模块来实现网络模型。

与其它深度学习库的对比

实战-使用PyTorch解决一个图像识别问题