强化学习通俗理解系列三：动态规划求解最优策略

黄海安

---

0 前言

       第二篇文章讲到了贝尔曼期望方程和贝尔曼最优方程，其中贝尔曼期望方程可以用于求解给定策略下，各状态的值函数大小，而贝尔曼最优方程可以用于求解最优策略。理论上是这样没错，但是实际应用还是要稍微再研究研究的，故而衍生出了后面一系列具体算法。本章是求解强化学习中的规划planning问题,也就是在已知模型的基础上判断一个策略的价值函数，并在此基础上寻找到最优的策略和最优价值函数，或者直接寻找最优策略和最优价值函数。本章内容在实际中应用不多，因为实际环境中模型通常是未知的，但是请不要小看这一章，它是学习后续Reinforcement Learning的前提，或者说引子，请务必重视！相应的，我给出本章的脑图(接第一篇文章总结部分的脑图)，让大家明白现在学习到哪里了：

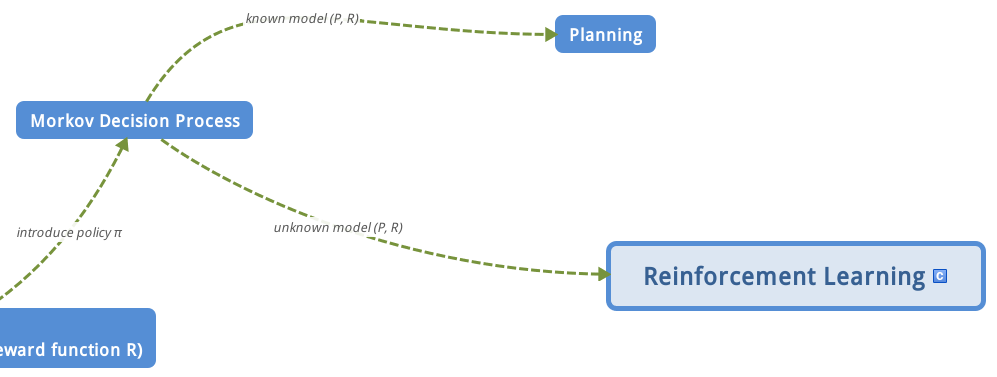
1 动态规划和规划问题定义

       本章实际上在求解Planning问题，看到上面的脑图，我想大家应该知道这章在干嘛了？其实就是在完成planning问题中的状态值函数求解和最优策略求解问题。而在planning中解决上述问题的方法叫做动态规划(Dynamic Programming,DP)，注意DP是一种思想，而不是指某一个具体算法，使用DP求解规划问题，依然要用到贝尔曼期望方程和贝尔曼最优方程。
       首先规划Planning问题的意思是：已知模型情况下求解最优值函数，包括状态值函数和行为值函数，和最优策略问题。模型已知是指我们对整个环境有充分了解，能够建立模型，更具体通俗来说就是P、R和Action是已知的，举上一章学生状态图的例子，那就是一个planning问题，因为每个状态下的状态转移概率、回报和行为空间都是已知了，也就是说上一章的最优策略问题，在本章中可以完美解决。
       那么动态规划DP是啥呢？大家不要感觉很高端，这里的动态规划和算法导论里面的动态规划是同一个东西，本质上是一种复杂问题简单化的思想。DP算法通过把复杂问题分解为子问题，通过求解子问题进而得到整个问题的解。在解决子问题的时候，其结果通常需要存储起来被用来解决后续复杂问题。一个复杂问题可以使用DP思想来求解，只要满足两个性质就可以：(1)一个复杂问题的最优解由数个小问题的最优解构成，可以通过寻找子问题的最优解来得到复杂问题的最优解；(2)子问题在复杂问题内重复出现，使得子问题的解可以被存储起来重复利用。
       基于马尔科夫决定过程（MDP）的planning问题正好满足上述两个特性：Bellman方程把问题递归为求解子问题，价值函数就相当于存储了一些子问题的解，可以复用。因此可以使用动态规划来求解MDP。
       一句话总结：在了解了整个MDP模型的基础上求解最优策略，那就是planning问题，只要有一个未知(P未知或者R未知或者Action未知)就不是planning问题，而且Reinforcement Learning问题。由于planning满足DP问题所必须的两个性质，所以通常求解planning问题是采用DP思想，其中应用DP还是要使用贝尔曼期望方程和贝尔曼最优方程。

2 Planning by Dynamic Programming

       这里给出planning问题的数学定义。

       planning问题具体可以分为预测prediction和控制control，其中prediction就是输入一个全模型的MDP、策略或者全模型的MRP，要通过DP算法求解得到值函数(也就是评估该策略的好坏)，说到底就是在已知模型情况下，通过DP求值函数；而control就是通过DP求最优策略。对于predication，是使用迭代策略评估(Iterative Policy Evaluation)算法求解；对于control，是通过策略迭代(Policy Iteration)，或者值迭代(Value Iteration)算法求解，后面会讲述两种求解算法的区别和联系。

3 策略估算Policy Evaluation

       策略估算准确来说是迭代策略估算。其标准定义是：

策略估算要解决的问题是评估给定策略的好坏，通过值函数大小来反映。具体解决思想是：采用DP思想，结合贝尔曼期望方程，对每次迭代求解得到的值函数进行备份backup，不断迭代，最终得到每个状态的值函数。上图中的同步synchronous是指对于第$k+1$次迭代，所有的状态s的价值用$v_k(s')$计算并更新，其中s’是s的后继状态，后面看到代码就明白了。
       下面来复习一些MDP下的贝尔曼期望方程：

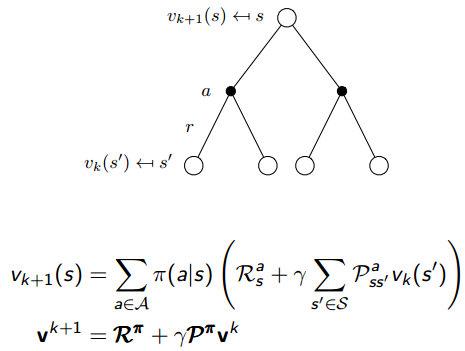
其中，有

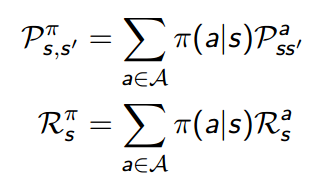
好了，有了上述公式，其实只要不断迭代就可以评估某一策略的值函数了。在大神的PPT里面举了一个方格世界的例子，通过该例子，大家可以非常清楚的知道迭代过程(下一篇文章就是通过视频来讲解本章内容代码，使读者能够深入理解)。其描述是：

我来简要描述一下：整个世界是方格世界，一共包括16种状态，其中左上角和右下角是终止状态，终止状态的立即回报是0，其余状态的立即回报是-1，折扣因子是1，对于每个状态，都有4种行为，分别是上下左右，并且采取每个行为的概率都是1/4，而且在不会出边界，例如状态1，如果它往上走，那么会直接返回到状态1，也就是这里有一个循环。现在问题是求在给定的随机策略下的值函数，或者说是策略评估。解决这个问题，就只需要上面的贝尔曼期望方程就可以。

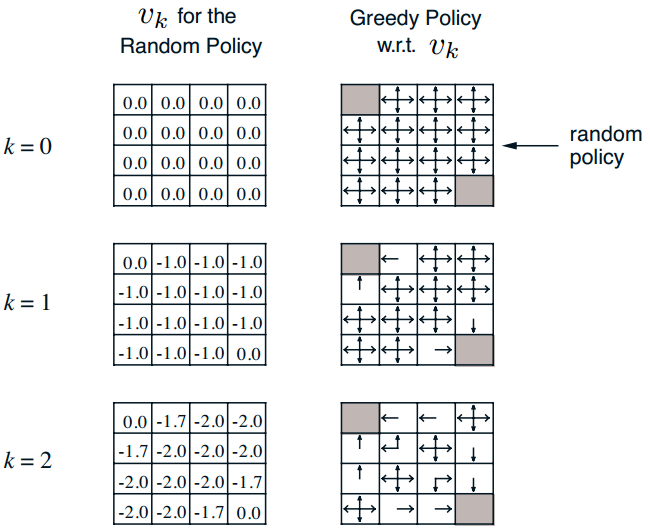
上图就是具体迭代过程(大家先不用管右边policy内容)，在k=0时候，所以状态的值函数全部初始化为0，好的，现在开始进入第一次迭代k=1;我以坐标为(1,0)状态为例，讲解下计算过程：
(1) k=1 (1,0)状态，为了方便写，我假设为s10=(1,0) .那么有

$$v(s10)=p(上|s10)*(-1+1 * 1×v(0,0))+p(下|s10)*(-1+1 * 1×v(2,0))$$ $$+p(左|s10)*(-1+1*1×v(1,0))+p(右|s10)*(-1+1 * 1×v(1,1))$$ $$=0.25*(-1+0)+0.25(-1+0)+0.25(-1+0)+0.25(-1+0)=-1$$

(2) k=2 (1,0)状态，那么有

$$v(s10)=p(上|s10)*(-1+1 * 1×v(0,0))+p(下|s10)*(-1+1 * 1×v(2,0))$$ $$+p(左|s10)*(-1+1*1×v(1,0))+p(右|s10)*(-1+1 * 1×v(1,1))$$ $$=0.25*(-1+0)+0.25(-1+-1)+0.25(-1+-1)+0.25(-1+-1)=-1.7$$

大家应该知道咋算了把！

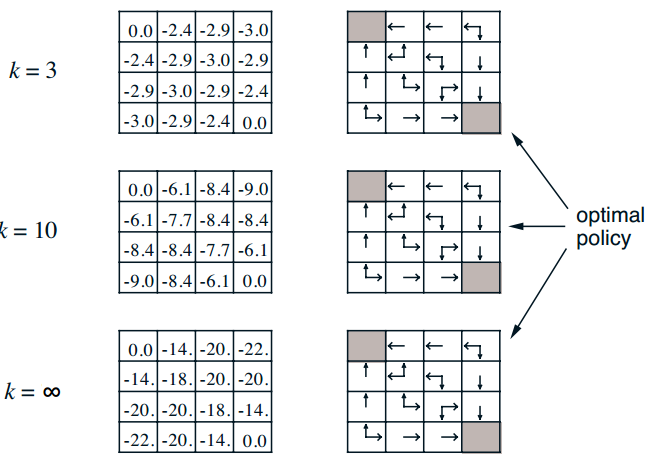
通过无数次迭代，最终可以收敛，具体数值如上图。是不是很简单，一直使用贝尔曼期望方程迭代就可以了。(附加一句：右边的policy图其意思是说通过不断求解值函数，其实就可以通过贪婪策略求解最优策略，其实也就是后面策略迭代要使用的算法)

4 策略迭代Policy Iteration

       现在我们已经能通过算法真正的通过迭代求解得到任意给定策略下的值函数了，也就是完成了策略评估部分。现在要开始进行策略改进(Policy Improvement)了，其中策略迭代Policy Iteration=策略评估Policy Evaluation(内层迭代)+策略提升Policy Improvement(外层迭代)。策略评估前面已经说了，策略提升其实更简单，只需要使用贪婪策略即可。即

$$\pi^{'}=greedy(v_{\pi})$$ 操作也非常简单，就是在每次评估得到值函数后，针对每个v(s),从里面选择一个action，使得下一时刻获得的回报最大，对选择出来的action，将其概率置1，其余action置0即可。贪婪策略是指每次选择的策略都是基于当前最优的策略。理论已经证明采用这种简单策略可以保证收敛到最优策略。

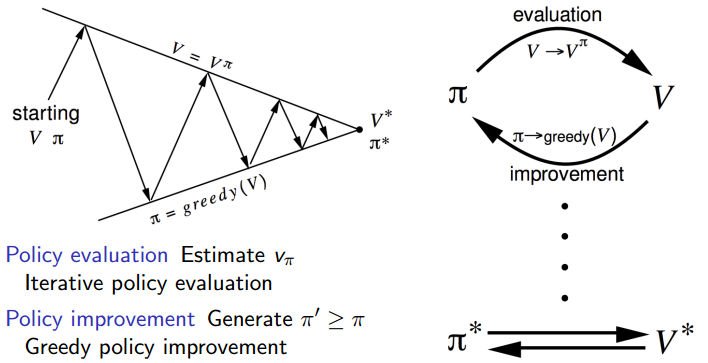
上图是一个非常经典的图，就是说明了不管你采用任意初始策略和值函数V，采用策略迭代算法一定能够收敛到最优策略和最优值函数。Divad Sliver的课程PPT中有详细证明，这里就不写了。

5 可修改的策略迭代Modified Policy Iteration

       很多时候，策略的更新较早就收敛至最优策略，而状态价值的收敛要慢很多，是否有必要一定要迭代计算直到状态价值得到收敛呢？答案是否定的，我们完全可以在迭代中间就停止，从而提前收敛。例如上面的方格世界例子，其实在k=3的时候就已经是最优策略了，但是状态值函数还远远没有收敛。根据这个原理，我们可以提出改善的策略迭代法。具体改进策略就多种多样了，例如可以引入一些停止条件，例如设定一个Ɛ，当值函数前后两次差值小于Ɛ时候停止；也可以直接设定为K步迭代，对于上面的方格世界例子，k=3就够了；当然也可以设置k=1，其实这就等价于值迭代算法了，下一节讲述。

6 值迭代

       首先把值迭代内容讲完，然后再分析策略迭代和值迭代的区别。
       值迭代算法是直接使用贝尔曼最优方程，而不像策略迭代那样，先使用贝尔曼期望方程，然后再使用贪婪策略。首先复习下贝尔曼最优方程：

值迭代法就是直接利用上述公式不断迭代即可。其标准定义如下：

可能大家看完上面公式，还是不知道代码咋写，或者说实际上是如何运行的，下一篇文章就是讲这快的代码。
       可以看出：策略迭代包括两层循环，其实策略的更新是显性操作，而值迭代法只有一层迭代，直接对值函数迭代，并没有显性的更新策略操作，所以这就是两者区别。值迭代法可以看出是策略迭代中的外层迭代k=1，然后把两次操作合并为一次迭代(是不是不好理解，其实我也不太理解)。

7 总结

       首先总结下本章内容，如下图：

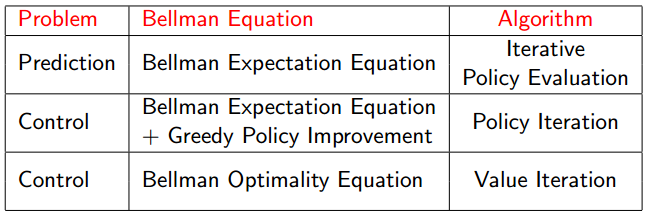
上面图其实写的非常清楚了。对于prediction问题，采用的算法是迭代策略估计，迭代方程是贝尔曼期望方程；对于control问题，有两种解法：策略迭代法，迭代方程是贝尔曼期望方程+贪婪策略提升；值迭代法，迭代方程是贝尔曼最优方程。
       下面给出planning问题的详细脑图，对应前言部分，希望能加深理解：

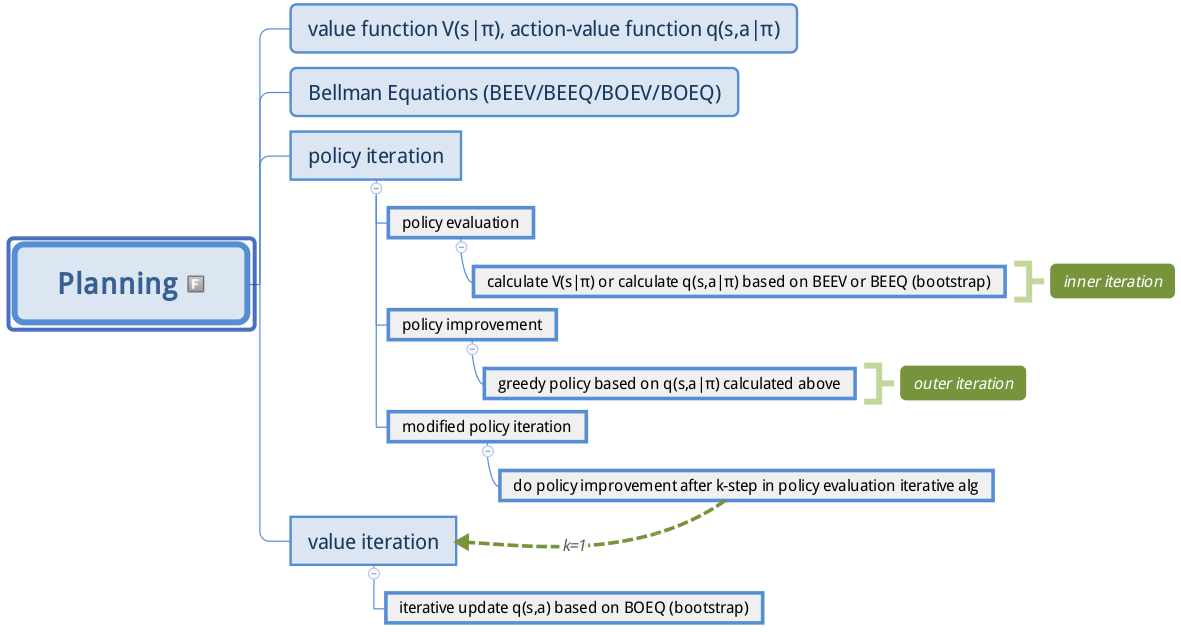
       下一章讲解本章的代码部分。由于水平有限，如有疑问，欢迎加群交流678455658。

参考文献

1 David Sliver 强化学习公开课，b站有视频