@Pigmon
2017-04-03T16:22:20.000000Z
字数 8959
阅读 1847
摄像机标定整理
CV
针孔相机模型
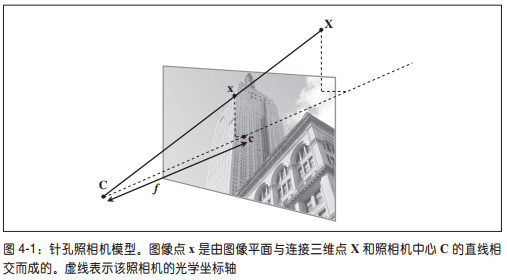
:三维点
:图像点
:相机中心
:光心(主点)
:焦距
三维点到图像点的投影计算
(4.1)
:三维点
:图像点
:三维点的逆深度
:相机矩阵(投影矩阵),3x4矩阵
相机矩阵的计算
基本形式:
:标定矩阵,描述照相机的投影性质
:旋转矩阵 3x3
:平移向量 3x1
标定矩阵
基本形式:
:纵横比例参数,在像素非正方形时使用,所以一般情况都是
:倾斜参数,表示像素数组在传感器上偏斜,所以一般情况都是
所以,的公式通常为:
和:光心的和坐标,通常情况下是图像的中心,可以由图像尺寸计算出来。
所以一般情况下,唯一的未知变量是焦距。
RQ 因子分解
因子分解即矩阵分块。这里是为了从中分离出和()。
待补充
计算照相机中心
是一个三维点,满足
即: (是正交矩阵,)
相机的中心和内标定矩阵无关。
以平面和标记物进行姿态估计
步骤:
- 拍摄一个矩形参照物正面的照片1
- 拍摄任意角度矩形参照物的照片2
- 提取两个图形的SIFT特征,进行图像配准
- 用RANSAC估计出两幅图像变换的单应性矩阵
- 定义照片1的三维坐标系,通过单应性矩阵映射出照片2对应的坐标系
- 令照片1中标记物平面为,设照片1的相机矩阵,计算过程待补充。
- 根据公式计算照片2的相机矩阵
增强现实实例
这一节完整的用PyGame和PyOpenGL做了一个简单的增强现实例子,前提应该是已知了变换的摄像机矩阵P,以及其分量K和Rt。
三维重建(多视图几何)
简单说,多视图几何就是通过分析在不同视点拍摄的同一地点的多张图像,来分析相机矩阵,以及图像的特征的学科。一般三维结构的信息是通过兴趣点来分析的,这本书也是。
目前多视图几何的主要内容是双视图几何。
外极几何 (Epipolar Geometry)
外极几何的简单示意图
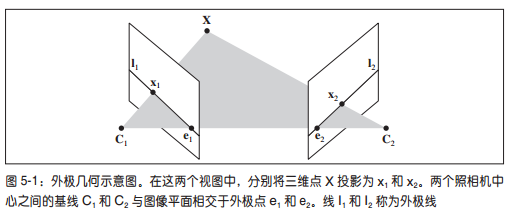
其中:
:三维点
:图像1的摄像机中心
:图像2的摄像机中心
:图像1的图像点
:图像2的图像点
:图像1的外极线
:图像2的外极线
:图像1的外极点
:图像1的外极点
基础矩阵 (Fundamental Metrix, Essential Matrix)
一般情况下,计算双视图几何的时候,为了简化,会将坐标轴与图像1的相机位置对齐,则:
其中是第二个相机的旋转矩阵,是第二个相机的平移向量。同时,它们也分别是第二个相机相对于第一个相机的旋转矩阵和平移向量。
同个三维点通过不同投影矩阵产生的图像点必须满足:
(外极约束条件公式,5.1)
其中为基础矩阵,公式为:
(行列式为0,秩小于等于2)
其中为反对称矩阵,公式为:
(5.2)
外极线
根据公式 ,令 得到 ,为图像1相对于图像2的图像点的外极线。这条直线由和两相机和的连线与图像1平面交点,即外极点确定,所以通过计算出以后,可以用来计算。
因为外极点在外极线上,满足, 所以和计算和。(把摄像机的位置视作三维点,则外极点为的图像点)
八点法(8-points Algorithm)
八点法的目的是求基础矩阵。(在平面场景中会失败)
基本八点法的步骤
基本原理
上面的外极约束条件公式: ,是一个关于的,含有9个未知数的齐次线性方程,由于在相差一个常数因子的意义下是唯一的(书上这里是写“因为尺度是任意的”。这里待补充),所以可以将其中的一个非零参数归一化而变为8个未知参数,因此如果能得到8对匹配点,就可以线性地确定。
步骤
为了表述方便,替换之前表述中的两个图像点和为和,用来表述它们的坐标分量。则外极约束条件公式变成:
其中,为2图像点的归一化坐标。
令
根据,得出:
令 为 的列向量模式,即:
令
则对任意匹配图像点对有:
----------------------------------------(式1)
因此,只要知道8对匹配点,就可以得到一个由8个形如(式1)的方程构成的线性方程组,在相差一个常数因子的意义下求出矩阵。如果匹配点对的数目多于8个,则可以利用最小二乘法求解。将n(n>8)个这样的方程叠起来得到线性方程组:
----------------------------------------(式2)
其中 -----代表第对匹配点的。
是一个矩阵,根据基础矩阵的定义,所有的解向量之间只相差一个常数因子(Why?)。为避免多余解,附加约束条件,则就是最小特征值对应的特征向量。(待补充)
设的(奇异值分解)为,其中,则,即求出了。(待补充)
零空间
一个算子的零空间是方程的所有解的集合。它也叫做的核, 核空间。用集合建造符号表示为:
凸集(convex set)
一个集合称为凸集,若对任意的两个点,连接他们的点都在集合内。
若从原点出发,并且通过该集合中任意一点的所有射线以及连接这些射线的任意两点的所有线段仍然在该凸集内,则该凸集可以称为凸锥。
凸包(Convex Hull)
在一个实数向量空间中,对于给定集合,所有包含的凸集的交集被称为X的凸包。
的凸包可以用X内所有点的线性组合来构造。
在二维欧几里得空间中,凸包可想象为一条刚好包著所有点的橡皮圈。
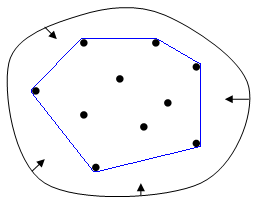
三角剖分(Triangulation)
简单说就是把点集或点云链接成一群三角形面组成的包围盒。
假设是二维实数域上的有限点集,边是由点集中的点作为端点构成的封闭线段, 为的集合。那么该点集V的一个三角剖分是一个平面图,该平面图满足条件:
1.除了端点,平面图中的边不包含点集中的任何点。
2.没有相交边。
3.平面图中所有的面都是三角面,且所有三角面的合集是散点集的凸包。
三角剖分在书中的应用
给定照相机参数模型,图像点可以通过三角剖分来恢复出这些点的三维位置。
由三维点计算照相机矩阵
如果已经知道了一些三维点及其图像投影,我们可以使用直接线性变换的方法来计算照相机矩阵P。本质上,这是三角剖分方法的逆问题,有时我们将其称为照相机反切法。利用该方法恢复照相机矩阵同样也是一个最小二乘问题。
我们从照相机方程( 4.1)可以得出,每个三维点 Xi(齐次坐标系下)按照投影到图像点,相应的点满足下面的关系:
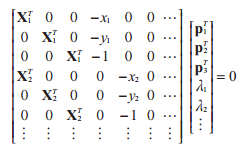
其中是矩阵的三行。简化为:
然后,我们可以使用 SVD 分解估计出照相机矩阵。
由基础矩阵计算照相机矩阵
在两个视图的场景中,照相机矩阵可以由基础矩阵恢复出来。假设第一个照相机矩阵归一化为 ,现在我们需要计算出第二个照相机矩阵。
未标定的情况——投影重建
在没有任何照相机内参数知识的情况下,照相机矩阵只能通过射影变换恢复出来。也就是说,如果利用照相机的信息来重建三维点,那么该重建只能由射影变换计算出来(你可以得到整个投影场景中无畸变的重建点)。在这里,我们不考虑角度和距离。
因此,在无标定的情况下,第二个照相机矩阵可以使用一个( 3×3)的射影变换得
出。一个简单的方法是:
其中,是左极点,满足, 是如公式(5.2)所示的反对称矩阵。请注意,使用该矩阵做出的三角形剖分很有可能会发生畸变,如倾斜的重建。
(5.2)
已标定的情况——度量重建
给定标定矩阵,我们可以将它的逆作用于图像点,因此,在新的图像坐标系下,照相机方程变为:
在新的图像坐标系下,点同样满足之前的基础矩阵方程:
在标定归一化的坐标系下,基础矩阵称为本质矩阵。为了区别为标定后的情况,以及归一化了的图像坐标,我们通常将其记为,而非。
从本质矩阵恢复出的照相机矩阵中存在度量关系,但有四个可能解。因为只有一个解产生位于两个照相机前的场景,所以我们可以轻松地从中选出来。
多视图重建
多视图重建是指超过2个视图的重建,一般是从视频中取帧进行重建,所以又被称为SfM( Structure from Motion,从运动中恢复结构)。
假设照相机已经标定,计算重建可以分为下面 4 个步骤:
(1) 检测特征点,然后在两幅图像间匹配;
(2) 由匹配计算基础矩阵;
(3) 由基础矩阵计算照相机矩阵;
(4) 三角剖分这些三维点。
Sampson 距离
待补充
多视图的延伸内容
多视图
视频:根据时序,在连续的帧之间匹配特征。相对方位从每个帧对增量的加入下一个帧对。误差会累积,最后需要有优化步骤。
静态图像:可以选择一个主参考图,计算其他图的相机矩阵。或者从一个图像对出发,增量加入新图像和三维点。另外还有针对3幅图像计算三维重建和照相机位置。
光束法平差(Bundle Adjustment)
多视图重建的最后一步,通常是通过优化三维点的位置和照相机参数来减少二次投影误差。
待补充
自标定
在未标定照相机的情形中,有时可以从图像特征来计算标定矩阵。该过程称为自标定。根据在照相机标定矩阵参数上做出的假设,以及可用的图像数据的类型(特征匹配、平行线、平面等),我们有很多不同的自标定算法。
待补充
立体视觉
假设得到对同一场景的2个视图,2个相机的Y轴没有相对移动,那么可以假设2个视图在同一个逻辑平面上,对应点也在同一条水平线上。
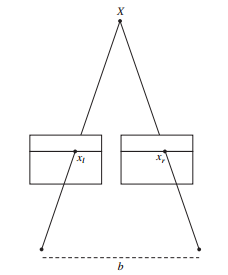
这样称2个视图经过了矫正。
在这种情况下,计算深度,即坐标可以通过以下公式:
来计算。其中是焦距,是两个相机之间的距离,和是两个图像点的轴坐标。相机之间的线段称为基线。
立体重建(有时称为致密深度重建)就是恢复深度图(或者相反,视差图),图像中每个像素的深度(或者视差)都需要计算出来。
图像间的匹配点检测
寻找相同的物体在不同图像上的对应的兴趣点。
兴趣点描述子
是分配给兴趣点的一个向量,描述该点附近的图像的表观信息。
Harris 角点的描述子通常由2部分:
- 角点为中心的像素块(nxn矩形区域)
- 归一化的互相关矩阵(用于比较)
简单说这个事情一般是这样:
对于2个图像,图像1中的任意兴趣点1,与图像2中的任意兴趣点2,先计算2个兴趣点各自像素块的相关性。如果相关性大于某个阈值认为相关,在2个点中间画条线。
的相关性数值是通过归一化相关矩阵给出的。
相关矩阵
两个大小相同的像素块()相关矩阵定义的一般形式:
书中对函数的选取为,则,其中为向量的点乘。的值越大,像素的相似度越高。
对于另一个常用的选取是
归一化相关矩阵
据说是为了让图像的亮度变化更“稳健”
这种方法出错率比较高,因为不具备尺度不变性和旋转不变性。
2.2 SIFT(Scale-Invariant Feature Transform,尺度不变特征变换)
SIFT 特征包括兴趣点检测器和描述子。SIFT描述子具有非常强的稳健性。SIFT特征对于尺度、旋转和亮度都具有不变性,因此,它可以用于三维视角和噪声的可靠匹配。
2.2.1 兴趣点
SIFT 特征使用高斯差分函数来定位兴趣点:
其中, 是二维高斯核, 是使用模糊的灰度图像, 是决定相差尺度的常数。
兴趣点是在图像位置和尺度变化下的最大值和最小值点。再通过某些滤波规则过滤掉其中一部分。
2.2.2 描述子
SIFT描述子包括兴趣点的如下信息:
- 位置
- 尺度
- 参考方向
参考方向是为了实现旋转不变性,参考方向基于兴趣点周围图像的梯度大小和方向计算。参考方向基于主方向描述,主方向使用方向直方图来度量。
不同于上面的Harris描述子使用亮度计算归一化相关矩阵,SIFT描述子使用图像梯度。
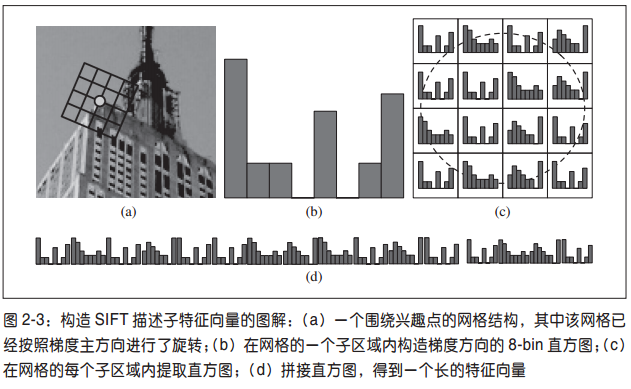
SIFT描述子简要计算过程
- 以兴趣点为中心选取4x4区域小方格
- 根据兴趣点梯度主方向旋转该4x4小方格区域
- 计算每个小方格梯度方向的8-bin直方图
- 把上面计算好的16个直方图连接起来成为描述子向量
SIFT描述子补充
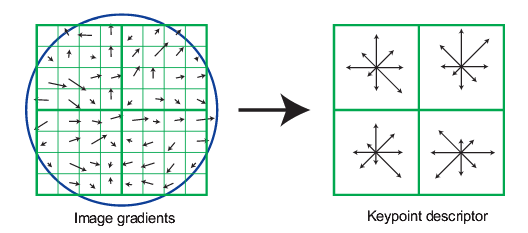
左图可以看作上图方格中的其中4个,其中每个方格中包含4x4个像素(每个小方格代表一个像素)。像素中的箭头代表梯度(方向,大小)。将方格中每个像素梯度按其分量大小累加到8个轴上,这样一个方格中就能累加出一个8-bin的直方图。如右图所示。
左图中的蓝色圈代表加权范围,离圆心(也就是兴趣点)越近的像素,其梯度的加权值越重。
图像配准
对于两张图像进行各种变换,使得两图像中的点对位置可以一一对应的过程。
比如,两张图像中,不同角度,不同尺度或在图像中的位置等不同因素拍摄的同一个人的脸,通过变换,把此人的两只眼睛的位置在两幅图像之间建立映射关系,以便后续的处理(比如一系列图像的主成分分析PCA)。
配准也可以针对不是同一个对象的情况,也比如人脸的例子,进行比较的未必属于同一个人。
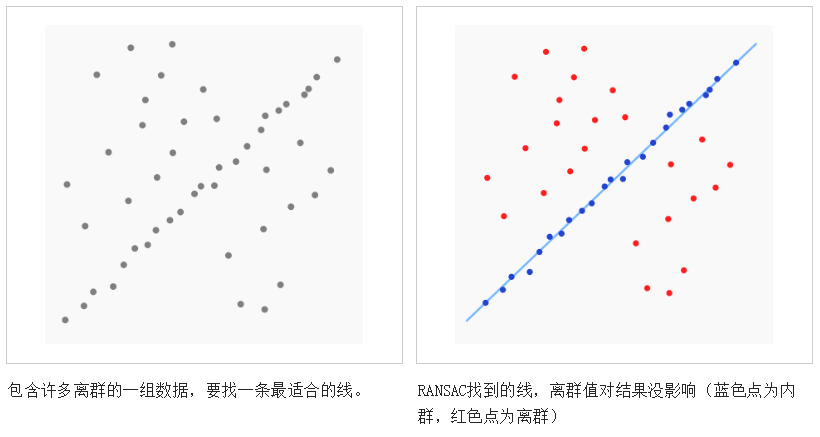
随机一致性采样(RANdom SAmple Consensus RANSAC)
随机抽样一致算法(RANdom SAmple Consensus,RANSAC)。它采用迭代的方式从一组包含离群的被观测数据中估算出数学模型的参数。 RANSAC是一个非确定性算法,在某种意义上说,它会产生一个在一定概率下合理的结果,而更多次的迭代会使这一概率增加。此RANSAC算法在1981年由Fischler和Bolles首次提出。
书中使用本算法达到估计出图像间的单应性矩阵的目的。
RANSAC的基本假设是
- “内群”数据可以通过几组模型的参数来叙述其分布,而“离群”数据则是不适合模型化的数据。
- 数据会受噪声影响,噪声指的是离群,例如从极端的噪声或错误解释有关数据的测量或不正确的假设。
- RANSAC假定,给定一组(通常很小)的内群,存在一个程序,这个程序可以估算最佳解释或最适用于这一数据模型的参数。
RANSAC优缺点
RANSAC的优点是它能鲁棒的估计模型参数。例如,它能从包含大量局外点的数据集中估计出高精度的参数。RANSAC的缺点是它计算参数的迭代次数没有上限;如果设置迭代次数的上限,得到的结果可能不是最优的结果,甚至可能得到错误的结果。RANSAC只有一定的概率得到可信的模型,概率与迭代次数成正比。RANSAC的另一个缺点是它要求设置跟问题相关的阀值。
RANSAC只能从特定的数据集中估计出一个模型,如果存在两个(或多个)模型,RANSAC不能找到别的模型。
最小二乘法
参考http://blog.csdn.net/wenrenhua08/article/details/2909255
根据变量的实测值对,可以用直角坐标系中一条直线来近似的描述的关系:
令直线的方程为:
----------------------------------(最1)
其中为任意实数。
算法的目的是为了确定以得到直线方程。
将测量值与计算值的离差的平方和最小化为优化判据。
令-----------------------------(最2)
将(最1)代入(最2)得:
---------------------(最3)
分别对求偏导,令两个偏导数为0,即:
-----------(最4)
--------(最5)
得到:
这样分别得到关于和的两个方程组,解得:
将(最8)(最9)代入(最1),得到回归的元线性方程。
在回归过程中,回归的关联式是不可能全部通过每个回归数据点,为了判断关联式的好坏,可借助相关系数,统计量,剩余标准偏差进行判断;越趋近于越好;的绝对值越大越好;越趋近于越好。
维基百科上最小二乘法应用在线性回归上的例子
某次实验得到了四个数据点 (图中红色的点)。我们希望找出一条和这四个点最匹配的直线 ,即找出在某种“最佳情况”下能够大致符合如下超定线性方程组的 和 :
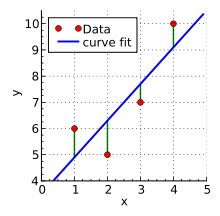
最小二乘法采用的手段是尽量使得等号两边的方差最小,也就是找出这个函数的最小值:
最小值可以通过对 分别求 和 的偏导数,然后使它们等于得到。
如此就得到了一个只有两个未知数的方程组,很容易就可以解出:
也就是说直线 是最佳的。