base_local_planner代码解析之一：trajectory_planner.cpp

ROS

可参考：https://blog.csdn.net/Neo11111/article/details/104713086/记录对trajectory_planner.cpp中定义的TrajectoryPlanner类的阅读和理解
可参考： https://blog.csdn.net/Neo11111/article/details/104720103记录对MapCell、MapGrid类和CostmapModel类阅读和理解。

trajectory_planner_ros和trajectory_planner关联紧密，产生轨迹、轨迹打分、选最好轨迹等函数都直接在这两个源文件里实现，footprint_helper、costmap_model、world_Model、trajectory、 map_grid，map_cell服务于trajectory_plannerp。

trajectory_planner_ros.cpp中定义了TrajectoryPlannerROS类，trajectory_planner.cpp中定义了TrajectoryPlanner类，MapGrid和MapCell类用于局部规划的计算，costmap_model.cpp中定义了CostmapModel类，它派生自WorldModel类，在TrajectoryPlanner中被使用，承担局部规划器与局部规划Costmap之间的桥梁工作。

trajectory_planner.cpp它是轨迹生成基本功能的实现程序，不同的局部轨迹规划方法（navfn::NavfnROS、carrot_planner::CarrotPlanner、dwa_local_planner::DWAPlannerROS或base_local_planner::TrajectoryPlannerROS），很多都要用到这个基本App中的函数

(1)
if (meter_scoring_) {

    //if we use meter scoring, then we want to multiply the biases by the resolution of the costmap
    double resolution = costmap_.getResolution();
    goal_distance_bias_ *= resolution;
    path_distance_bias_ *= resolution;
  }

gen.add("oscillation_reset_dist", double_t, 0, "The distance the robot must travel before oscillation flags are reset, in meters", 0.05, 0, 5)

• @param path_distance_bias A scaling factor for how close the robot should stay to the path
• @param goal_distance_bias A scaling factor for how aggresively the robot should pursue a local goal
• @param occdist_scale A scaling factor for how much the robot should prefer to stay away from obstacles
• @param heading_lookahead How far the robot should look ahead of itself when differentiating between different rotational velocities
• @param oscillation_reset_dist The distance the robot must travel before it can explore rotational velocities that were unsuccessful in the past
• @param escape_reset_dist The distance the robot must travel before it can exit escape mode
• @param escape_reset_theta The distance the robot must rotate before it can exit escape mode
• @param heading_scoring Set this to true to score trajectories based on the robot's heading after 1 timestep
• @param heading_scoring_timestep How far to look ahead in time when we score heading based trajectories

(2)costmap_2d::calculateMinAndMaxDistances(footprint_spec_, inscribed_radius_, circumscribed_radius_);//Calculate the extreme distances for the footprint

void calculateMinAndMaxDistances(const std::vector<geometry_msgs::Point>& footprint, double& min_dist, double& max_dist)
{
  min_dist = std::numeric_limits<double>::max();//numeric_limits<double>::max () 是函数,返回编译器允许的 double 型数 最大值。 
  max_dist = 0.0;

  if (footprint.size() <= 2)
  {
    return;
  }

  for (unsigned int i = 0; i < footprint.size() - 1; ++i)
  {
    // check the distance from the robot center point to the first vertex
    double vertex_dist = distance(0.0, 0.0, footprint[i].x, footprint[i].y);

    double edge_dist = distanceToLine(0.0, 0.0, footprint[i].x, footprint[i].y,
                                      footprint[i + 1].x, footprint[i + 1].y);
    min_dist = std::min(min_dist, std::min(vertex_dist, edge_dist));
    max_dist = std::max(max_dist, std::max(vertex_dist, edge_dist));
  }

  // we also need to do the last vertex and the first vertex
  double vertex_dist = distance(0.0, 0.0, footprint.back().x, footprint.back().y);
  double edge_dist = distanceToLine(0.0, 0.0, footprint.back().x, footprint.back().y,
                                      footprint.front().x, footprint.front().y);
  min_dist = std::min(min_dist, std::min(vertex_dist, edge_dist));
  max_dist = std::max(max_dist, std::max(vertex_dist, edge_dist));
}





 double distanceToLine(double pX, double pY, double x0, double y0, double x1, double y1)
{
  double A = pX - x0;
  double B = pY - y0;
  double C = x1 - x0;
  double D = y1 - y0;

  double dot = A * C + B * D;
  double len_sq = C * C + D * D;
  double param = dot / len_sq;

  double xx, yy;

  if (param < 0)
  {
    xx = x0;
    yy = y0;
  }
  else if (param > 1)
  {
    xx = x1;
    yy = y1;
  }
  else
  {
    xx = x0 + param * C;
    yy = y0 + param * D;
  }

  return distance(pX, pY, xx, yy);
}

(3)//the robot is not stuck to begin with机器人没有被卡住

  bool stuck_left, stuck_right; ///< @brief Booleans to keep the robot from oscillating during rotation
  bool rotating_left, rotating_right; ///< @brief Booleans to keep track of the direction of rotation for the robot

  bool stuck_left_strafe, stuck_right_strafe; ///< @brief Booleans to keep the robot from oscillating during strafing
  bool strafe_right, strafe_left; ///< @brief Booleans to keep track of strafe direction for the robot   布尔值，用于跟踪机器人的行进方向

（4） bool TrajectoryPlanner::getCellCosts(int cx, int cy, float &path_cost, float &goal_cost, float &occ_cost, float &total_cost)获取每个栅格的代价值，由三个代价值构成
- @param path_cost Will be set to the path distance component of the cost function
* @param goal_cost Will be set to the goal distance component of the cost function
* @param occ_cost Will be set to the costmap value of the cell
* @param total_cost Will be set to the value of the overall cost function, taking into account the scaling parameters
* @return True if the cell is traversible and therefore a legal location for the robot to move to

 if (cell.within_robot) {
        return false;
    }


occ_cost = costmap_.getCost(cx, cy);
path_cost = cell.target_dist;//不是直线距离，是和A*类似的格子传播距离，斜的可不可以走？？？
goal_cost = goal_cell.target_dist;//局部地图的goal
total_cost = path_distance_bias_ * path_cost + goal_distance_bias_ * goal_cost + occdist_scale_ * occ_cost;

上面是将来可以修改的地方！！！！！！
注释：

**target_dist** ///< @brief Distance to planner's path or to goal

unsigned char* Costmap2D::getCharMap() const
{
  return costmap_;
}

unsigned map2D::getCost(unsigned int mx, unsigned int my) const
{
  return costmap_[getIndex(mx, my)];
}

void Costmap2D::setCost(unsigned int mx, unsigned int my, unsigned char cost)
{
  costmap_[getIndex(mx, my)] = cost;//看每个栅格的cost怎么算出来的？？？？？？？？？
}

namespace costmap_2d
   {
        static const unsigned char NO_INFORMATION = 255;
        static const unsigned char LETHAL_OBSTACLE = 254;
        static const unsigned char INSCRIBED_INFLATED_OBSTACLE = 253;
        static const unsigned char FREE_SPACE = 0;

    }

（5）void TrajectoryPlanner::generateTrajectory(
double x, double y, double theta,
double vx, double vy, double vtheta,
double vx_samp, double vy_samp, double vtheta_samp,
double acc_x, double acc_y, double acc_theta,
double impossible_cost,
Trajectory& traj)

这个函数根据给定的速度和角速度采样生成单条路径和其代价。该函数被**double TrajectoryPlanner::**scoreTrajectory(double x, double y, double theta, double vx, double vy,
double vtheta, double vx_samp, double vy_samp, double vtheta_samp)函数和Trajectory TrajectoryPlanner::createTrajectories(double x, double y, double theta,
double vx, double vy, double vtheta,
double acc_x, double acc_y, double acc_theta) 调用；

而该scoreTrajectory(--）函数被bool TrajectoryPlanner::checkTrajectory(double x, double y, double theta, double vx, double vy, double vtheta, double vx_samp, double vy_samp, double vtheta_samp)函数调用。

而 createTrajectories被Trajectory TrajectoryPlanner::findBestPath(const geometry_msgs::PoseStamped& global_pose, geometry_msgs::PoseStamped& global_vel, geometry_msgs::PoseStamped& drive_velocities)调用。

 double vmag = hypot(vx_samp, vy_samp);
//compute the number of steps we must take along this trajectory to be "safe"
int num_steps;
if(!heading_scoring_) {
      num_steps = int(max((vmag * sim_time_) / sim_granularity_, fabs(vtheta_samp) / angular_sim_granularity_) + 0.5);//在这里heading_scoring_原始设置为false,sim_granularity_代表仿真点之间的距离间隔
    } else {
      num_steps = int(sim_time_ / sim_granularity_ + 0.5);//在这里heading_scoring_为true, sim_granularity_代表仿真的时间间隔
}

double dt = sim_time_ / num_steps;

上面是将来可以修改的地方！！！

 //check the point on the trajectory for legality
  double footprint_cost = footprintCost(x_i, y_i, theta_i);

//footprintCost与world_model.h紧密相连，整个world_model.h就是计算footprintCost的， return Positive if all the points lie outside the footprint, negative otherwise:
* -1 if footprint covers at least a lethal obstacle cell, or
* -2 if footprint covers at least a no-information cell, or
* -3 if footprint is partially or totally outside of the map

//if the footprint hits an obstacle this trajectory is invalid
  if(footprint_cost < 0){
    traj.cost_ = -1.0;

//有多少num_step ，就考虑路径轨迹上有多少个点。将路径上点的最大cost记录在occ_cost中，这一步完成了碰撞检测的工作。
//更新occ_cost：max(max(occ_cost，路径足迹代价)，当前位置的代价)
//也就是把所有路径点的最大障碍物代价设置为路径的occ_cost

occ_cost = std::max(std::max(occ_cost, footprint_cost), double(costmap_.getCost(cell_x, cell_y)));

接下来考虑与全局路径及目标点的距离：
如果simple_attractor_开启，采用比较简单的追踪策略，只考虑与目标点之间的直线距离^2
如果simple_attractor_未开启，则借助goal_map_和path_map_获取该点与目标点及全局规划路径之间的距离，若超过范围，说明没有明确的目标路径，则该路径无效，直接返回-2.0
经过迭代，goal_dist和path_dist储存的都是路径上最后一个点的对应代价，也就是用这种方法评价一条路径时，若路径有效，【全局路径及目标点的距离】只与路径末点有关。
如果开启heading_scoring_即为朝向打分，只有当从开始生成该条路径计时，到达特定时刻时，才会进行唯一一次打分，headingDiff函数的具体过程是：
从全局路径终点（目标点）开始，当前点与全局路径上的各点依次连线获得cost，cost为正（无障碍）则立即计算：当前点与迭代到的点间的连线方向与当前点的姿态之差，返回给heading_diff并停止继续连线；
若所有连线cost都为负，返回极大值。
为朝向打分的轮次将不更新goal_dist和path_dist。轮次时间间隔大小为heading_scoring_timestep_

// with heading scoring, we take into account heading diff, and also only score
// path and goal distance for one point of the trajectory

  //在这里heading_scoring_原始设置为true时zh 
if (heading_scoring_) {
  if (time >= heading_scoring_timestep_ && time < heading_scoring_timestep_ + dt) {
    heading_diff = headingDiff(cell_x, cell_y, x_i, y_i, theta_i);
  } else {
    update_path_and_goal_distances = false;
  }
}

  double TrajectoryPlanner::headingDiff(int cell_x, int cell_y, double x, double y, double heading){
unsigned int goal_cell_x, goal_cell_y;

// find a clear line of sight from the robot's cell to a farthest point on the path
for (int i = global_plan_.size() - 1; i >=0; --i) {
  if (costmap_.worldToMap(global_plan_[i].pose.position.x, global_plan_[i].pose.position.y, goal_cell_x, goal_cell_y)) {
    if (lineCost(cell_x, goal_cell_x, cell_y, goal_cell_y) >= 0) {
      double gx, gy;
      costmap_.mapToWorld(goal_cell_x, goal_cell_y, gx, gy);
      return fabs(angles::shortest_angular_distance(heading, atan2(gy - y, gx - x)));
    }
  }
}
return DBL_MAX;

}

//使用heading_scoring,但要去掉下面的0.3 * heading_diff，或把0.3调小

double cost = -1.0;
if (!heading_scoring_) {
  cost = path_distance_bias_ * path_dist + goal_dist * goal_distance_bias_ + occdist_scale_ * occ_cost;
} else {
  cost = occdist_scale_ * occ_cost + path_distance_bias_ * path_dist + 0.3 * heading_diff + goal_dist * goal_distance_bias_;
}

任何一个点的if(impossible_cost <= goal_dist || impossible_cost <= path_dist),则轨迹舍掉： //impossible_cost = path_map_.obstacleCosts()，obstacleCosts()==map_.size()

          if(impossible_cost <= goal_dist || impossible_cost <= path_dist){
//            ROS_DEBUG("No path to goal with goal distance = %f, path_distance = %f and max cost = %f",
//                goal_dist, path_dist, impossible_cost);
            traj.cost_ = -2.0;
            return;
          }

一条备选轨迹的最终cost取的是最后一个点的cost,很不好，可以改进！！！

if (!heading_scoring_) {
  cost = path_distance_bias_ * path_dist + goal_dist * goal_distance_bias_ + occdist_scale_ * occ_cost;
} else {
  cost = occdist_scale_ * occ_cost + path_distance_bias_ * path_dist + 0.3 * heading_diff + goal_dist * goal_distance_bias_;
}
traj.cost_ = cost;

经过检测，若该点足迹不遇障，且该点的goal_dist与path_dist存在，加入轨迹。

traj.addPoint(x_i, y_i, theta_i);

经过检测，若该点足迹不遇障，且该点的goal_dist与path_dist存在，加入轨迹。
并通过函数计算该点的速度，速度计算函数使当前速度在dt时间内以加速度acc_x向采样速度靠近，到达采样速度后将不再改变。所以实际上每条轨迹都是一个由当前速度趋向并稳定在采样速度的过程。
接下来通过航迹推演公式计算下一个路径点的坐标，并将几个打分的项按比例加和，得到当前路径的cost，进入下一次迭代，循环往复填充路径坐标，并更新路径cost。
需要注意的是，这里对速度的计算与我们发布给机器人的速度无关，这里的速度只是为了推算下一个点，获得路径，而我们真正发布给机器人的速度是采样速度。真实世界里机器人由当前速度–>采样速度的过程对应我们地图上本次仿真的轨迹。

-

（6）void TrajectoryPlanner::updatePlan(const vector& new_plan, bool compute_dists)
* @brief Update the plan that the controller is following
* @param new_plan A new plan for the controller to follow
* @param compute_dists Wheter or not to compute path/goal distances when a plan is updated
*
*

（7） **Trajectory TrajectoryPlanner::createTrajectories(double x, double y, double theta,
double vx, double vy, double vtheta,
double acc_x, double acc_y, double acc_theta)
* @brief Create the trajectories we wish to explore, score them, and return the best option

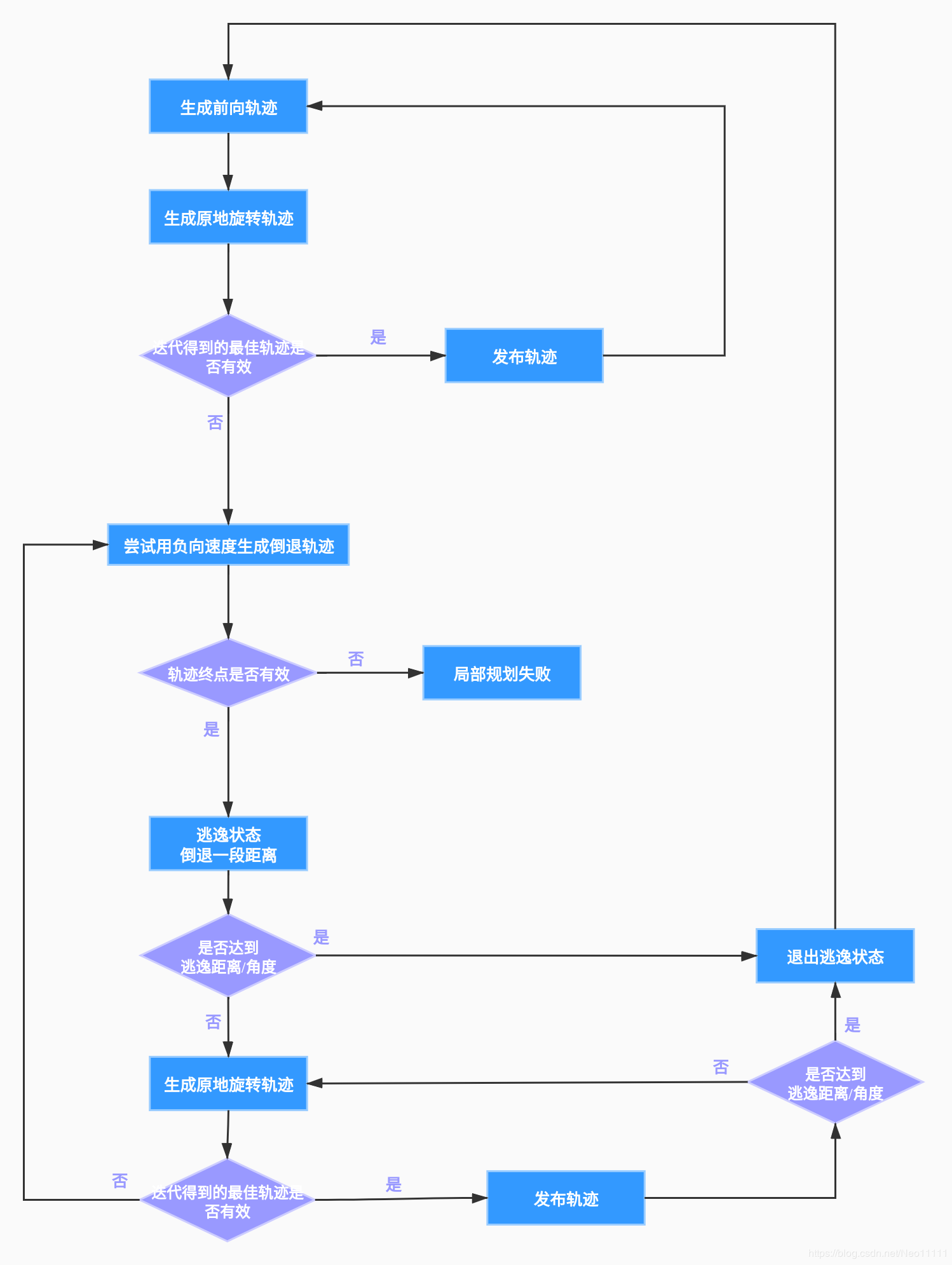
//< @brief final_goal_position_valid_ is True if final_goal_x_ and final_goal_y_ have valid data. Only false if an empty path is sent.也就是说最大速度还是要根据终点位置再算的，即保证速度既不超过预设的最大速度限制，也不超过“起点与目标直线距离/总仿真时间”。

 if( final_goal_position_valid_ ){
          double final_goal_dist = hypot( final_goal_x_ - x, final_goal_y_ - y );
          max_vel_x = min( max_vel_x, final_goal_dist / sim_time_ );
        }

//should we use the dynamic window approach?
//继续计算线速度与角速度的上下限，使用的限制是由当前速度在一段时间内，由最大加减速度达到的速度范围，这里进行了一个判断，即是否使用dwa法：
① 使用dwa法，则用的是轨迹前向模拟的周期sim_period_（专用于dwa法计算速度的一个时间间隔）；
② 不使用dwa法，则用的是整段仿真时间sim_time_
在生成范围时同时考虑用预先给定的速度和角速度范围参数进行保护。

 if (dwa_) {
      max_vel_x = max(min(max_vel_x, vx + acc_x * sim_period_), min_vel_x_);
      min_vel_x = max(min_vel_x_, vx - acc_x * sim_period_);

      max_vel_theta = min(max_vel_th_, vtheta + acc_theta * sim_period_);
      min_vel_theta = max(min_vel_th_, vtheta - acc_theta * sim_period_);
    } else {
      max_vel_x = max(min(max_vel_x, vx + acc_x * sim_time_), min_vel_x_);
      min_vel_x = max(min_vel_x_, vx - acc_x * sim_time_);

      max_vel_theta = min(max_vel_th_, vtheta + acc_theta * sim_time_);
      min_vel_theta = max(min_vel_th_, vtheta - acc_theta * sim_time_);
    }

//接下来根据预设的线速度与角速度的采样数，和上面计算得到的范围，分别计算出采样间隔，并把范围内最小的线速度和角速度作为初始采样速度。不考虑全向机器人的情况，即不能y向移动，故暂不考虑vy上采样。  
     //we want to sample the velocity space regularly
    double dvx = (max_vel_x - min_vel_x) / (vx_samples_ - 1);
    double dvtheta = (max_vel_theta - min_vel_theta) / (vtheta_samples_ - 1);

    double vx_samp = min_vel_x;
    double vtheta_samp = min_vel_theta;
    double vy_samp = 0.0;

    vtheta_samp += dvtheta;
    vx_samp += dvx;

  Trajectory* best_traj = &traj_one;
  best_traj->cost_ = -1.0;//先初始化一个最优路径的代价=-1
  Trajectory* comp_traj = &traj_two; //下面生成的轨迹放到这里，和best_traj作比较，如果生成的轨迹代价更小，就选择它
  comp_traj->cost_ = -1.0;//先初始化一个当前“对比”路径的代价=-1，等会再用generateTrajectory函数生成路径和新的代价存放在里面

接下来，在机器人没有处于逃逸状态时，开始遍历所有线速度和角速度，调用类内generateTrajectory函数用它们生成轨迹。二重迭代时，外层遍历线速度（正值），内层遍历角速度。在遍历时，单独拎出角速度=0，即直线前进的情况，避免由于采样间隔的设置而跃过了这种特殊情况。
边迭代生成边比较，获得代价最小的路径，存放在best_traj。
执行完成后，也跳出了“未处于逃逸状态”这个判断结构。

//next we want to generate trajectories for rotating in place

 vtheta_samp = min_vel_theta;//min_vel_theta可以大于也可以小于0，注意配置文件中怎么办？？？？？？？？？？？？？？？


    //let's try to rotate toward open space
    double heading_dist = DBL_MAX;

    for(int i = 0; i < vtheta_samples_; ++i) {
      //enforce a minimum rotational velocity because the base can't handle small in-place rotations。在处理这种情况时，由于机器人原地旋转时的角速度限制范围要比运动时的角速度限制范围更严格，底盘无法处理过小的原地转速，故要注意处理这层限制。
      double vtheta_samp_limited = vtheta_samp > 0 ? max(vtheta_samp, min_in_place_vel_th_)
        : min(vtheta_samp, -1.0 * min_in_place_vel_th_);

      generateTrajectory(x, y, theta, vx, vy, vtheta, vx_samp, vy_samp, vtheta_samp_limited,
          acc_x, acc_y, acc_theta, impossible_cost, *comp_traj);//尤其注意

    if (dist > escape_reset_dist_ ||
    fabs(angles::shortest_angular_distance(escape_theta_, theta)) > escape_reset_theta_) {
  escaping_ = false;
}//escape_reset_dist_不能设太小

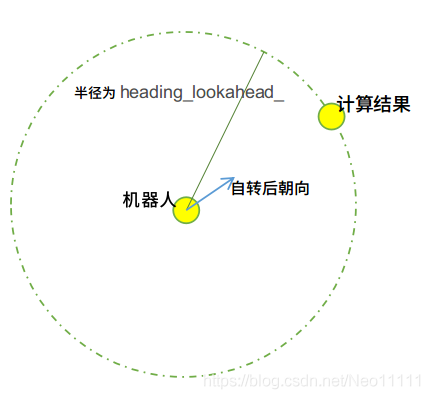
//下面，它获取旋转后的“面向”的栅格位置坐标，实际上也就是原地的x、y坐标，再加上heading_lookahead_×自转后姿态的三角函数（下面代码的5，6，7行），这个坐标跟原地的坐标关系如下（下面代码的5，6，7行）：

if(comp_traj->cost_ >= 0
          && (comp_traj->cost_ <= best_traj->cost_ || best_traj->cost_ < 0 || best_traj->yv_ != 0.0)
          && (vtheta_samp > dvtheta || vtheta_samp < -1 * dvtheta)){
        double x_r, y_r, th_r;
        comp_traj->getEndpoint(x_r, y_r, th_r);
        x_r += heading_lookahead_ * cos(th_r);
        y_r += heading_lookahead_ * sin(th_r);
        unsigned int cell_x, cell_y;

    //make sure that we'll be looking at a legal cell即要求原地旋转后“面向“的栅格在地图中，且该位置所在栅格到路径终点可达（下面三行）
    if (costmap_.worldToMap(x_r, y_r, cell_x, cell_y)) {
      double ahead_gdist = goal_map_(cell_x, cell_y).target_dist;
      if (ahead_gdist < heading_dist) {

            //所以经过迭代，必然会筛选掉计算结果是障碍物的情形（上面一行），也就是机器人旋转后不会面向障碍物；同时筛选后，也能得到和目标点距离最短的计算结果，保证机器人在旋转后向前行进，距离目标点的路程更短（下面第5行）。
            if (vtheta_samp < 0 && !stuck_left) {
              swap = best_traj;
              best_traj = comp_traj;
              comp_traj = swap;
              heading_dist = ahead_gdist;
            }
            //if we haven't already tried rotating right since we've moved forward
            else if(vtheta_samp > 0 && !stuck_right) {
              swap = best_traj;
              best_traj = comp_traj;
              comp_traj = swap;
              heading_dist = ahead_gdist;
            }
          }
        }

轨迹生成已完成，接下来的工作可以概括为，如果轨迹cost非负，即找到有效轨迹，则将其返回；若找不到有效轨迹，进入逃逸状态，后退、原地自转，若找不到下一步的有效路径则再后退、自转，直到后退的距离或转过的角度达到一定标准，才会退出逃逸状态，重新规划前向轨迹。其中再加上震荡抑制。

     if (best_traj->cost_ >= 0) {
  // avoid oscillations of in place rotation and in place strafing
      //下面一行代码“当采样速度v≤0” ，由于线速度采样范围是正的，当出现非正采样速度时，只可能是上一次的traj无效，发布了后退命令，进入逃逸模式，然后重新循环，跳过前向轨迹规划，进入原地自转模式，导致采样速度=0。
所以可以说是，当原地自转时：
若角速度<0，标记rotating_right为真
若角速度>0，标记rotating_left为真
并记录当前自转的位置。
  if ( ! (best_traj->xv_ > 0)) {
    if (best_traj->thetav_ < 0) {
      if (rotating_right) {
        stuck_right = true;
      }
      rotating_right = true;
    } else if (best_traj->thetav_ > 0) {
      if (rotating_left){
        stuck_left = true;
      }
      rotating_left = true;
    } else if(best_traj->yv_ > 0) {
      if (strafe_right) {
        stuck_right_strafe = true;
      }
      strafe_right = true;
    } else if(best_traj->yv_ < 0){
      if (strafe_left) {
        stuck_left_strafe = true;
      }
      strafe_left = true;
    }

    //set the position we must move a certain distance away from标记震荡位置
    prev_x_ = x;
    prev_y_ = y;
  }

  }//以上的代码抑制震荡影响：当机器人在某方向移动时，对下一个周期的与其相反方向标记为无效

  //以下的代码直到机器人从标记震荡的位置处离开一定距离，返回最佳轨迹。
  double dist = hypot(x - prev_x_, y - prev_y_);
  if(dist > oscillation_reset_dist_) {
    rotating_left = false;
    rotating_right = false;
    strafe_left = false;
    strafe_right = false;
    stuck_left = false;
    stuck_right = false;
    stuck_left_strafe = false;
    stuck_right_strafe = false;
  }

  //若找不到有效轨迹，进入逃逸状态，后退、原地自转，若找不到下一步的有效路径则再后退、自转，直到后退的距离或转过的角度达到一定标准，才会退出逃逸状态，重新规划前向轨迹。
  dist = hypot(x - escape_x_, y - escape_y_);
  if(dist > escape_reset_dist_ || fabs(angles::shortest_angular_distance(escape_theta_, theta)) > escape_reset_theta_) {
    escaping_ = false;
  }

后面跳过完整机器人代码，发现出现了和上面笔记近似的代码，这是针对全向机器人算出来的轨迹的。不是全向的都执行到这的程序了，说明cost<0,也要越过的，不起作用。

轨迹有效的部分结束，当轨迹cost为负即无效时，执行接下来的部分，设置一个负向速度，产生让机器人缓慢退后的轨迹。此处也还是判断一下震荡距离。这就解释了为什么要往左拐一下，是不是因为震荡距离达到后才能后退，所以震荡距离设小点。

若后退速度生成的轨迹的终点有效（>-2.0），进入逃逸状态，循环后退、自转，并且记录下的逃逸位置和姿态，只有当离开逃逸位置一定距离或转过一定角度，才能退出逃逸状态（逃逸距离和角度参数要加大），再次规划前向速度。逃逸判断和震荡判断一样，也已在上面多次执行，只要发布best_traj前就执行一次判断。

若终点无效，返回负cost，本次局部规划失败。