Variational Mode Decomposition

数学

---

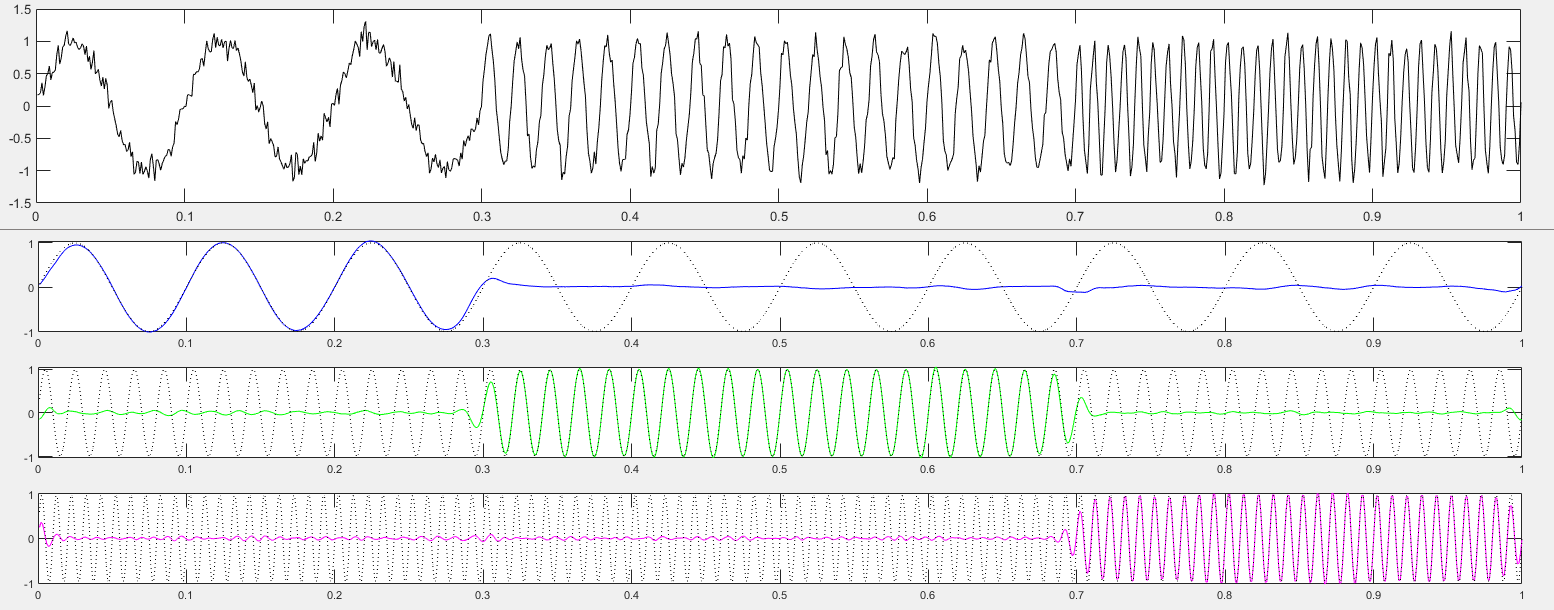
这一篇写一下变分模态分解（原始论文：Variational Mode Decomposition），跟原始论文思路思路一致但有一点点不太一样，原始论文写的很好，但我不是通信专业没有学过信号相关课程一开始看起来有点费劲。模态分解认为信号是由不同“模态”的子信号叠加而成的，而变分模态分解则认为信号是由不同频率占优的子信号叠加而成的，其目的是要把信号分解成不同频率的子信号。变分模态分解的分解结果如图所示

基础

一开始论文看不懂的原因是缺少相关前置知识，但一旦顺下来就会感觉其实没有那么难，难的是作者的思路很巧妙，先写下我遇到的这些知识盲点

第一点是傅立叶变换的微分性质，$f(t)$的傅立叶变换为$F(\omega)$，其导数$f'(t)$的傅立叶变换为$j\omega F(\omega)$

$$\begin{align*} f(t) &= \frac{1}{\sqrt{2\pi}} \int_\mathbb{R}F(\omega)e^{j\omega t}\mathrm{d}\omega \\ \frac{\partial f(t)}{\partial t} &= \frac{1}{2\pi}\int_\mathbb{R}\frac{\partial F(\omega)e^{j\omega t}}{\partial t} \mathrm d\omega \\ & = \frac{1}{2\pi} \int_\mathbb{R} j\omega F(\omega)e^{j\omega t}\mathrm d \omega \end{align*}$$

另一点是解析信号，现实世界只能采集实信号，但实信号有很多不好用的性质，如存在负频率，无法直接得到调制频率后的实信号等。
设原始信号是一个实信号

$$f(t) = A(t)\cos(\phi t)$$ 为了方便表示$\phi$为随$x$变化的函数，相当于瞬时频率，解析信号是一个复信号，可以通过希尔伯特变换得到
$$f_A(t) = f(t) + j\mathcal{H}f(t) = A(t)e^{j\phi t}$$ 解析信号的实部是原本的实数信号，并且经过调频之后复数信号的实部仍然是调频之后的实信号，如对信号$F_A(t)$增加频率$\omega_0$，只需要乘以$e^{j\omega_0 t}$即可
$$\begin{align*} f_A(t)\cdot e^{j\omega_0 t} & = A(t)e^{j\phi t} \cdot e{j\omega_0 t} \\ & = A(t)\cdot e^{j(\phi + \omega_0)t} \\ \Re {\Large\{} F_A(t)e^{j\omega_0 t} {\Large\}} & = A(t)\cdot \cos((\phi+\omega_0)t) \end{align*}$$ 由此，其实部相当于在原本频率$\phi$的基础上增加了频率$\omega_0$，如下面的matlab脚本

clear;close all;clc;
t = 1:0.01:10;
%%
f1 = sin(20*t).*(t-5).^2;
subplot(3,1,1);
plot(f1);
ylim([-25 25]);
%%
f2 = sin(50*t).*(t-5).^2;
subplot(3,1,2);
plot(f2);
ylim([-25 25]);
%%
H = hilbert(f1);
f_hat = H.*exp(1i*30.*t);
subplot(3,1,3);
plot(real(f_hat));
ylim([-25 25]);

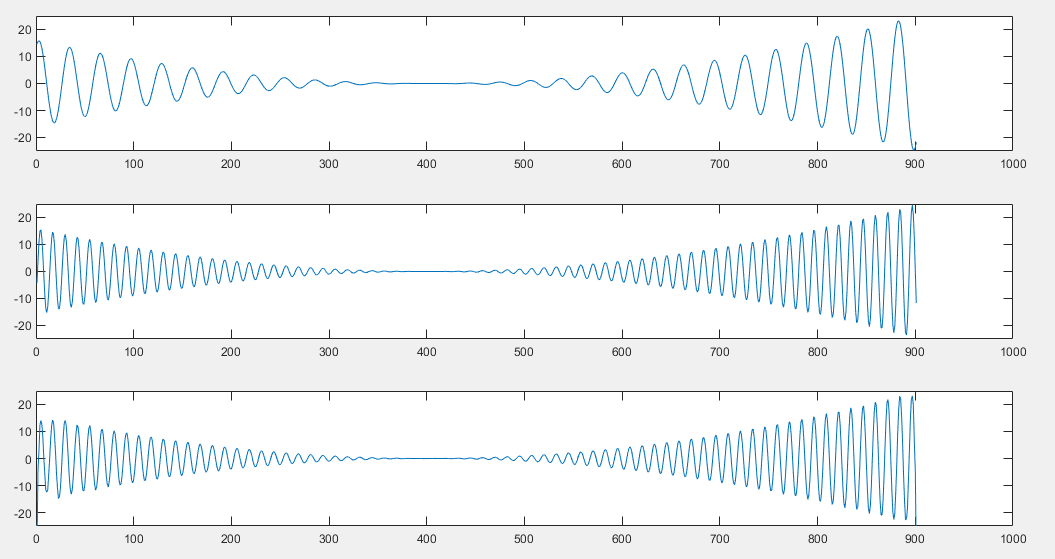
matlab的hilbert函数包括希尔伯特变换和解析函数转换两部分，直接得到实信号的解析信号，其中希尔伯特变换

$$\mathcal{H} f = \frac{1}{\pi} * f$$

正文

接下来我们看看如何一步一步得到变分模态分解的思路

原论文通过一个信号降噪问题进行说明，现需要对采样信号$f_0$进行降噪重构，假设观测信号是由原始信号叠加一个独立的高斯噪音

$$f_0 = f + \eta$$ ，需要求$f$，又说该等式是一个不适定问题（ill-posed problem），不满足识定问题的三个条件，所以要用一个正则化的方法
$$\underset{f}{\min}{\Large\{} \left \| f-f_0 \right \|_2^2 + \alpha \left \| \partial_t f \right \|_2^2 {\Large\}}$$ 第一部分是对原信号进行重构，第二部分是为了解决不适定问题的解不唯一，而且不同于机器学习的建模问题一样$f$是一个权值形式可以直接加权值$W$的L1-norm或L2-norm，这里的$f$是一个纯函数的形式，其导数的L2-norm最小化感觉上应该是保证了函数$f$不会产生太大的波动，这里可不可以跟防止过拟合联系起来，接下来说明这个约束会使$f$在频率域产生什么影响。

下面解这个式子，首先来看一下直接最小化泛函$J$能不能解出来

$$\begin{align*} J[f] &= \int_\mathbb{R}(f(t) - f_0(t))^2 + \alpha (f'(t))^2 \mathrm{d}t \\ & = \int_\mathbb{R}F(f, f')\mathrm{d}t \end{align*}$$ 有$F(f,f') = (f-f_0)^2 + \alpha(f')^2$，然后根据E-L方程的引理
$$\frac{\partial F}{\partial f'} f' - F = C$$ 得
$$\alpha{f'}^2 - (f-f_0)^2 = C$$ ，往下忘了怎么求了。。。。。想起来怎么求再继续写-_-!，这个直接求的方法与原文没什么关系的

由上面的傅立叶变换的微分性质知道，用傅立叶变换在复数域很方便可以把微分约掉，而且还有一个叫什么Plancherel傅立叶等距映射的东西，时域的L2范数与傅立叶变换到的频率域的L2范数等距，故上面的最小化的项可以直接用傅立叶变换转换到频域

$$\underset{\hat{f}(\omega)}{\min}{\Large\{} \left \| \hat{f}(\omega)-\hat{f_0}(\omega) \right \|_2^2 + \alpha \left \| j\omega\hat{f}(\omega) \right \|_2^2 {\Large\}}$$ ，这里需要注意的是利用上面的那个什么等距定理有$\hat{f}(\omega)$和$\hat{f_0}(\omega)$的$\omega$是同一个$\omega$，这一点很重要，第二个是L2范数大于0，则把其展开为泛函
$$J[\hat{f}] = \int_\mathbb{R}(\hat{f}(\omega) - \hat{f_0}(\omega))^2 + \alpha\omega^2(\hat{f}(\omega))^2 \mathrm{d}\omega$$ 求最极值，由于这里面只有$\hat{f}$直接求偏导即可也不用解微分方程
$$\begin{align*} \frac{\delta J[\hat{f}]}{\delta \hat{f}} &= 2(\hat{f} - \hat{f_0}) + 2\alpha\omega^2\hat{f} \\ &= 2(\hat{f}(1+\alpha\omega^2) - \hat{f_0}) = 0 \\ \hat{f} &= \frac{\hat{f_0}}{1 + \alpha\omega^2} \end{align*}$$

可以看到得到的$\hat{f}$相当于对观测信号在$\hat{f_0}$在频率段进行滤波，过滤掉了高频部分，这说明加了该导数的L1正则约束与上面的直观感觉是一样的，过滤掉了高频部分，减弱$f$的波动

再往下进行，模态分解需要把原始信号分解成多个子信号的和，我们为了和原文对应修改一下符号表示，$f(t)$表示观测的采样信号，$u_k(t)$表示分解得到的基函数，则上面的约束对象变为

$$\underset{u_k}{\min} {\Large\{} || \sum_k u_k(t) - f(t)||_2^2 + \alpha\sum_k|| \partial_ t [u_k(t)] ||_2^2 {\Large\}}$$ 同样先转化为频率域再求极值
$$\underset{\hat{u_k}}{\min} {\Large\{} || \sum_k \hat{u_k}(\omega) - \hat{f}(\omega)||_2^2 + \alpha\sum_k|| j\omega \hat{u_k}(\omega) ||_2^2 {\Large\}}$$ 泛函
$$J[\hat{u_1}, \hat{u_2}, \cdots,\hat{u_K}] = \int_\mathbb{R}(\sum_k\hat{u_k}(\omega) - \hat{f}(\omega))^2 + \alpha\omega^2\sum_k(\hat{u_k}(\omega))^2 \mathrm{d}\omega$$

$$\begin{align*} \frac{\delta J}{\delta u_k} &= 2 \left(\sum_k \hat{u_k} - \hat{f}\right) + 2 \alpha \omega \left(\hat{u_k} \right) = 0 \\ \hat{u_k}(\omega) &= \frac{\hat{f}(\omega) - \sum_{i\neq k}\hat{u_i}(\omega)}{1 + \alpha \omega^2} \end{align*}$$ 每个基函数基于其他的基函数更新，相当于每个基函数是原信号剩余部分的低通滤波，每次迭代都是保留剩余信号的低频率部分。

到现在为止我们发现每个基函数都会趋向于每次的剩余信号分量的低频部分，这与我们原始的假设“每个基函数都有不同的频率分量”是相悖的，但根据上面的低通滤波的性质，每个基函数进行特定频率的滤波应该就能解决这个问题了，那么上面的式子就简单的变为

$$\hat{u_k}(\omega) = \frac{\hat{f}(\omega) - \sum_{i\neq k}\hat{u_i}(\omega)}{1 + \alpha (\omega - \omega_k)^2}$$ 其中，$\omega_k$为每个基函数$u_k$的中心频率，该式就是变分模态分解的基函数的更新公式，我们来看一下这个式子应该如何得到，以便于找到中心频率的更新公式

由上面的一步一步的演化发现，基函数对剩余信号的低通滤波是由导数的L2正则最小化带来的，要得到基函数的中心频率约束也要从这个地方入手，由上面的推导可知每个基函数都会被约束到$0$频率附近，那么我们把基函数的频率增加各自的中心频率$\omega_k$得到$\hat{u_k}(\omega+\omega_k)$，并保证$\omega \geq 0$即可，则相当于对每个基函数乘以了一个$e^{-j\omega_k t}$，这里需要对频率进行变换，我们沿用文章开头的解析信号的性质，认为$u_k(t)$是一个复数的解析信号，同样也需要把观测信号$f$预先转化为解析信号，下文默认都是解析信号，则每一个基函数转换频率后的导数变为

$$\partial_t u_k(t) e^{-j\omega_k t}$$ 傅立叶变换得
$$j\omega\hat{u_k}(\omega+\omega_k)$$ 先来看看傅立叶变换为什么会得到这个，而不是$j(\omega + \omega_k)\hat{u_k}(\omega+\omega_k)$
反傅立叶变换
$$\begin{align*} u_k(t) &= \int_0^\infty\hat{u_k}(\omega+\omega_k)e^{j\omega t}\mathrm{d}\omega \\ \partial_t u_k(t) & = \int_0^\infty j\omega \hat{u_k}(\omega+\omega_k)e^{j\omega t}\mathrm{d}\omega \end{align*}$$ 感觉应该不是这样证的，我数学不是很好，不怎么会这个变量变换

至此，约束变为

$$\underset{u_k}{\min} {\Large\{} || \sum_k u_k(t) - f(t)||_2^2 + \alpha\sum_k\left\| \partial_ t \left[u_k(t)e^{-j\omega_k t}\right] \right\|_2^2 {\Large\}}$$
傅立叶变换
$$\underset{\hat{u_k}}{\min} {\Large\{} || \sum_k \hat{u_k}(\omega) - \hat{f}(\omega)||_2^2 + \alpha\sum_k\| j\omega \hat{u_k}(\omega + \omega_k) \|_2^2 {\Large\}}$$ 根据论文原文把$\omega\leftarrow \omega - \omega_k$
$$\underset{\hat{u_k}}{\min} {\Large\{} || \sum_k \hat{u_k}(\omega) - \hat{f}(\omega)||_2^2 + \alpha\sum_k\| j(\omega - \omega_k) \hat{u_k}(\omega) \|_2^2 {\Large\}}$$ 然后求最小就可以得到上面$\hat{u_k}$的更新公式
$$J = \int_0^\infty(\sum_k\hat{u_k}(\omega) - \hat{f}(\omega))^2 + \alpha\sum_k(\omega - \omega_k)^2(\hat{u_k}(\omega))^2 \mathrm{d}\omega$$

$$\begin{align*} \frac{\delta J}{\delta \omega_k} &= \int_0^\infty 2(\omega - \omega_k)|\hat{u_k}(\omega)|^2\mathrm{d}\omega \\ \omega_k &= \frac{\int_0^\infty \omega |\hat{u_k}(\omega)|^2\mathrm{d}\omega}{\int_0^\infty |\hat{u_k}(\omega)|^2\mathrm{d}\omega} \end{align*}$$

最后，为了保证每个点处的重构信号与原信号尽可能相似，增加了每个点处的重构约束，其实这一项并不是必需的，最终的约束对象为

$$\begin{multline*} \underset{\{u_k\},\{\omega_k\}}{\min} {\Large \{} || \sum_k u_k(t) - f(t)||_2^2 + \alpha\sum_k\left\| \partial_ t \left[u_k(t)e^{-j\omega_k t}\right] \right\|_2^2 {\Large \}} \\ s.t. \quad f = \sum_k u_k \end{multline*}$$ ，然后拉格朗日乘子法带进去，但其需要满足下式才有意义
$$\int_\mathbb{R} \lambda(t)\left( f(t) - \sum_k u_k(t) \right)\mathrm{d} t = \int_\mathbb{R} \hat{\lambda}(\omega)\left( \hat{f}(\omega) - \sum_k \hat{u_k}(\omega)\right)\mathrm{d}\omega$$ 这个式子还是符合Parseval定理，故整理一下
$$\begin{multline*} J = \int_0^\infty \alpha\sum_k(\omega - \omega_k)^2(\hat{u_k}(\omega))^2 + \left(\sum_k\hat{u_k}(\omega) - \hat{f}(\omega)\right)^2 \\ + \hat{\lambda}(\omega)\left( \hat{f}(\omega) - \sum_k \hat{u_k}(\omega)\right) \mathrm{d}\omega \end{multline*}$$

最后整理一下更新公式：

$$\hat{u_k}(\omega) = \frac{\hat{f}(\omega) - \sum_{i\neq k}\hat{u_i}(\omega) - \frac{\hat{\lambda}(\omega)}{2}}{1 + \alpha (\omega - \omega_k)^2} \\ \omega_k = \frac{\int_0^\infty \omega|\hat{u_k}(\omega)|^2 \mathrm{d}\omega}{\int_0^\infty |\hat{u_k}(\omega)|^2 \mathrm{d}\omega} \\ \hat{\lambda}^{n+1}(\omega) = \hat{\lambda}^n (\omega) - \tau\left( \hat{f}(\omega) - \sum_k \hat{u_k}(\omega) \right)$$ 其中$\hat{\lambda}$使用梯度下降更新

代码

%matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
from scipy.signal import hilbert

T = 1000
fs = 1./T
t = np.linspace(0, 1, 1000,endpoint=True)

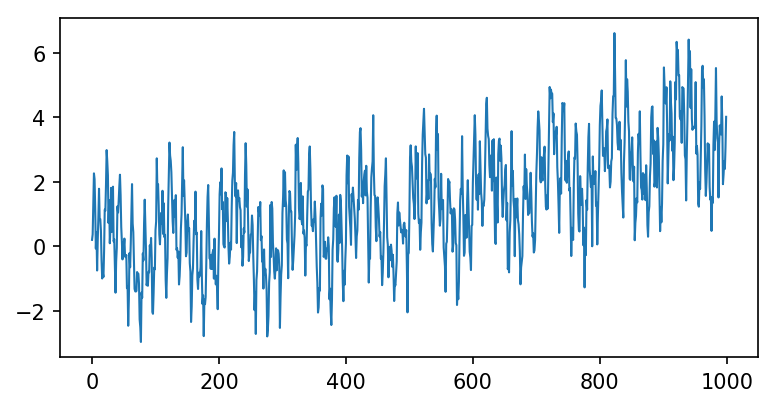
f_1 = 10
f_2 = 50
f_3 = 100
mode_1 = (2 * t) ** 2
mode_2 = np.sin(2 * np.pi * f_1 * t)
mode_3 = np.sin(2 * np.pi * f_2 * t)
mode_4 = np.sin(2 * np.pi * f_3 * t)
f = mode_1 + mode_2 + mode_3 + mode_4 + 0.5 * np.random.randn(1000)

plt.figure(figsize=(6,3), dpi=150)
plt.plot(f, linewidth=1)

[<matplotlib.lines.Line2D at 0x7fac533f6780>]

class VMD:
    def __init__(self, K, alpha, tau, tol=1e-7, maxIters=200, eps=1e-9):
        """
        :param K: 模态数
        :param alpha: 每个模态初始中心约束强度
        :param tau: 对偶项的梯度下降学习率
        :param tol: 终止阈值
        :param maxIters: 最大迭代次数
        :param eps: eps
        """
        self.K =K
        self.alpha = alpha
        self.tau = tau
        self.tol = tol
        self.maxIters = maxIters
        self.eps = eps
    def __call__(self, f):
        T = f.shape[0]
        t = np.linspace(1, T, T) / T
        omega = t - 1. / T
        # 转换为解析信号
        f = hilbert(f)
        f_hat = np.fft.fft(f)
        u_hat = np.zeros((self.K, T), dtype=np.complex)
        omega_K = np.zeros((self.K,))
        lambda_hat = np.zeros((T,), dtype=np.complex)
        # 用以判断
        u_hat_pre = np.zeros((self.K, T), dtype=np.complex)
        u_D = self.tol + self.eps
        # 迭代
        n = 0
        while n < self.maxIters and u_D > self.tol:
            for k in range(self.K):
                # u_hat
                sum_u_hat = np.sum(u_hat, axis=0) - u_hat[k, :]
                res = f_hat - sum_u_hat
                u_hat[k, :] = (res - lambda_hat / 2) / (1 + self.alpha * (omega - omega_K[k]) ** 2)
                # omega
                u_hat_k_2 = np.abs(u_hat[k, :]) ** 2
                omega_K[k] = np.sum(omega * u_hat_k_2) / np.sum(u_hat_k_2)
            # lambda_hat
            sum_u_hat = np.sum(u_hat, axis=0)
            res = f_hat - sum_u_hat
            lambda_hat -= self.tau * res
            n += 1
            u_D = np.sum(np.abs(u_hat - u_hat_pre) ** 2)
            u_hat_pre[::] = u_hat[::]
        # 重构，反傅立叶之后取实部
        u = np.real(np.fft.ifft(u_hat, axis=-1))
        omega_K = omega_K * T
        idx = np.argsort(omega_K)
        omega_K = omega_K[idx]
        u = u[idx, :]
        return u, omega_K

K = 4
alpha = 2000
tau = 1e-6
vmd = VMD(K, alpha, tau)

u, omega_K = vmd(f)

omega_K

array([0.85049797, 10.08516203, 50.0835613, 100.13259275]))

plt.figure(figsize=(5,7), dpi=200)
plt.subplot(4,1,1)
plt.plot(mode_1, linewidth=0.5, linestyle='--')
plt.plot(u[0,:], linewidth=0.2, c='r')
plt.subplot(4,1,2)
plt.plot(mode_2, linewidth=0.5, linestyle='--')
plt.plot(u[2,:], linewidth=0.2, c='r')
plt.subplot(4,1,3)
plt.plot(mode_3, linewidth=0.5, linestyle='--')
plt.plot(u[1,:], linewidth=0.2, c='r')
plt.subplot(4,1,4)
plt.plot(mode_4, linewidth=0.5, linestyle='--')
plt.plot(u[3,:], linewidth=0.2, c='r')

[<matplotlib.lines.Line2D at 0x7fac532f4dd8>]

---

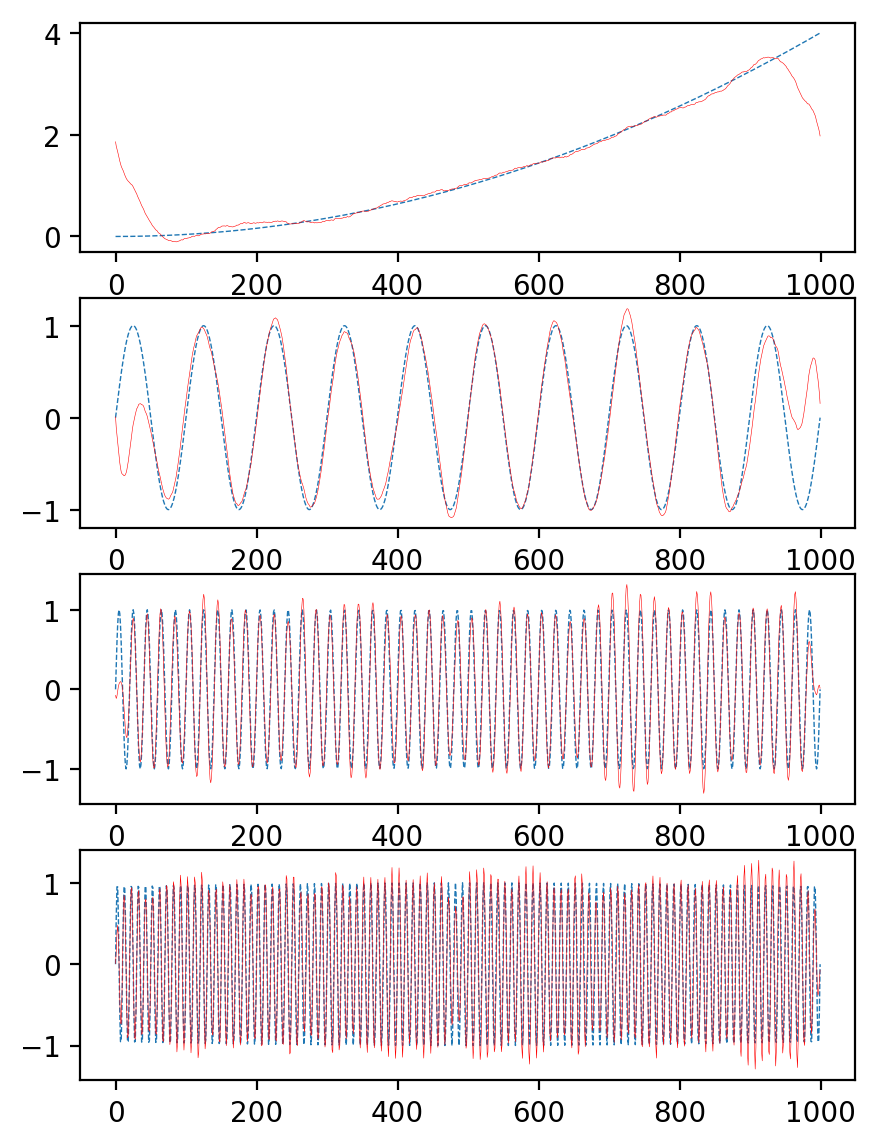
可以看到有比较强的端点效应，端点处会有重叠，文章原始论文中采用的方法是对称拼接的方法，把原信号复制一份然后拼成两半，一半对称放前面，一般对称放后面

%matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
from scipy.signal import hilbert

T = 1000
fs = 1./T
t = np.linspace(0, 1, 1000,endpoint=True)

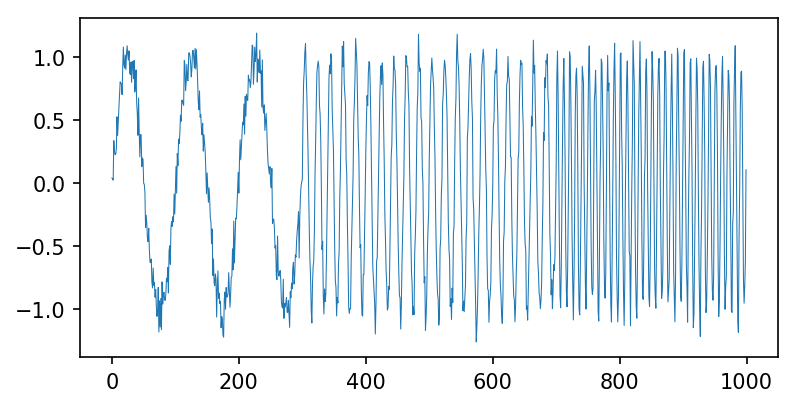
f_1 = 10
f_2 = 50
f_3 = 100
mode_1 = np.sin(2 * np.pi * f_1 * t)
mode_2 = np.sin(2 * np.pi * f_2 * t)
mode_3 = np.sin(2 * np.pi * f_3 * t)
f = np.concatenate((mode_1[:301], mode_2[301:701], mode_3[701:])) + 0.1 * np.random.randn(1000)

plt.figure(figsize=(6,3), dpi=150)
plt.plot(f, linewidth=0.5)

[<matplotlib.lines.Line2D at 0x7fc2134b8630>]

class VMD:
    def __init__(self, K, alpha, tau, tol=1e-7, maxIters=200, eps=1e-9):
        """
        :param K: 模态数
        :param alpha: 每个模态初始中心约束强度
        :param tau: 对偶项的梯度下降学习率
        :param tol: 终止阈值
        :param maxIters: 最大迭代次数
        :param eps: eps
        """
        self.K =K
        self.alpha = alpha
        self.tau = tau
        self.tol = tol
        self.maxIters = maxIters
        self.eps = eps
    def __call__(self, f):
        N = f.shape[0]
        # 对称拼接
        f = np.concatenate((f[:N//2][::-1], f, f[N//2:][::-1]))
        T = f.shape[0]
        t = np.linspace(1, T, T) / T
        omega = t - 1. / T
        # 转换为解析信号
        f = hilbert(f)
        f_hat = np.fft.fft(f)
        u_hat = np.zeros((self.K, T), dtype=np.complex)
        omega_K = np.zeros((self.K,))
        lambda_hat = np.zeros((T,), dtype=np.complex)
        # 用以判断
        u_hat_pre = np.zeros((self.K, T), dtype=np.complex)
        u_D = self.tol + self.eps
        # 迭代
        n = 0
        while n < self.maxIters and u_D > self.tol:
            for k in range(self.K):
                # u_hat
                sum_u_hat = np.sum(u_hat, axis=0) - u_hat[k, :]
                res = f_hat - sum_u_hat
                u_hat[k, :] = (res - lambda_hat / 2) / (1 + self.alpha * (omega - omega_K[k]) ** 2)
                # omega
                u_hat_k_2 = np.abs(u_hat[k, :]) ** 2
                omega_K[k] = np.sum(omega * u_hat_k_2) / np.sum(u_hat_k_2)
            # lambda_hat
            sum_u_hat = np.sum(u_hat, axis=0)
            res = f_hat - sum_u_hat
            lambda_hat -= self.tau * res
            n += 1
            u_D = np.sum(np.abs(u_hat - u_hat_pre) ** 2)
            u_hat_pre[::] = u_hat[::]
        # 重构，反傅立叶之后取实部
        u = np.real(np.fft.ifft(u_hat, axis=-1))
        u = u[:, N//2 : N//2 + N]
        omega_K = omega_K * T / 2
        idx = np.argsort(omega_K)
        omega_K = omega_K[idx]
        u = u[idx, :]
        return u, omega_K

K = 3
alpha = 2000
tau = 1e-6
vmd = VMD(K, alpha, tau)

u, omega_K = vmd(f)

omega_K

array([  9.64477193,  50.06365397, 100.18114375])

plt.figure(figsize=(5,7), dpi=200)
plt.subplot(3,1,1)
plt.plot(mode_1, linewidth=0.5, linestyle='--')
plt.plot(u[0,:], linewidth=0.2, c='r')
plt.subplot(3,1,2)
plt.plot(mode_2, linewidth=0.5, linestyle='--')
plt.plot(u[1,:], linewidth=0.2, c='r')
plt.subplot(3,1,3)
plt.plot(mode_3, linewidth=0.5, linestyle='--')
plt.plot(u[2,:], linewidth=0.2, c='r')

[<matplotlib.lines.Line2D at 0x7fc2134075c0>]

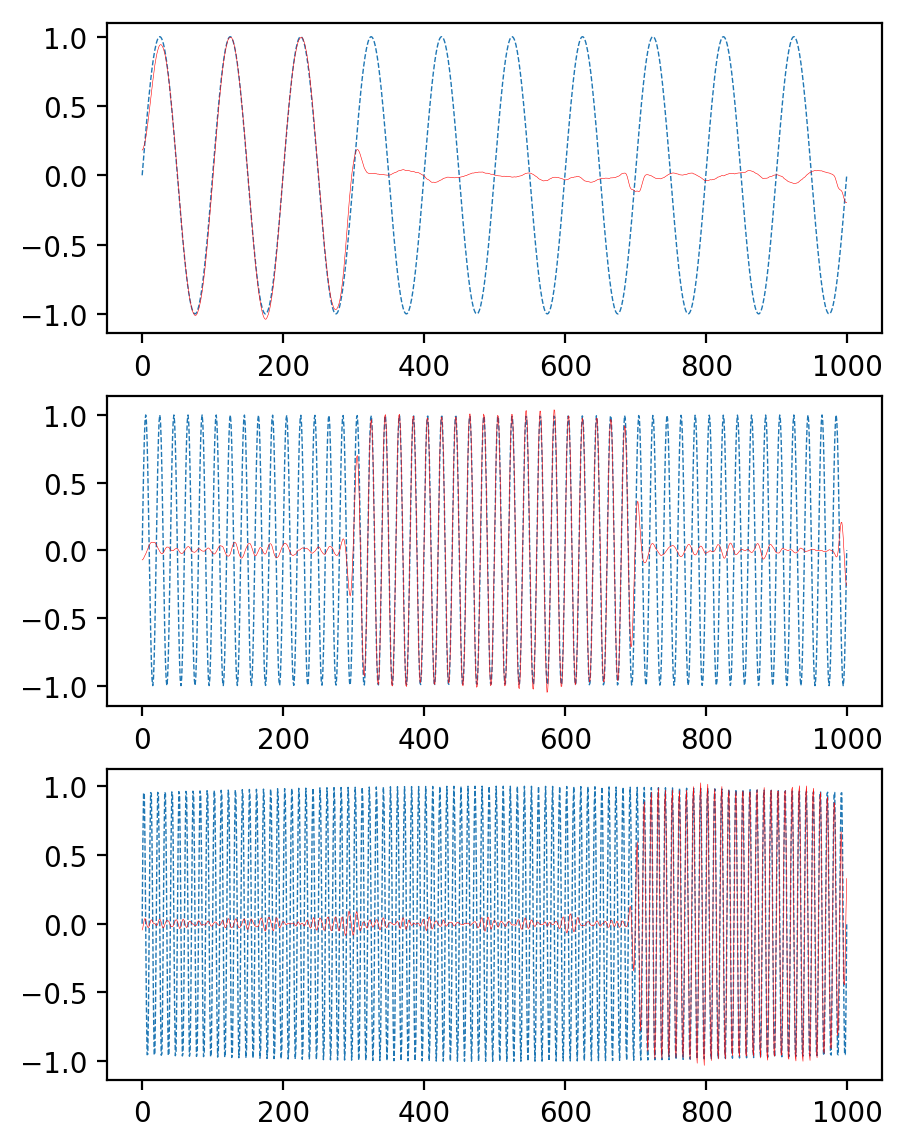
好像结果要好一点，VMD的一个缺点是K的值对结果有很大影响，但这个迭代过程，怎么开始怎么迭代怎么结束都可以自己控制，感觉可以按照自己的需求来定制怎么动态决定K

---