@zsh-o
2018-04-11T13:45:36.000000Z
字数 2105
阅读 2565
归一化确定均值和方差且最大化熵的概率分布为 正太分布(借助mathematica)
PRML 机器学习
《PRML》习题2.14,把多元概率分布改为了一维的,就是说只证一维的
概率分布的熵为
现在对这个概率分布有三个约束条件:
求证,使熵最大时的概率分布为正太分布
要求概率分布的具体形式,很容易想到用变分法来解,把熵看作是函数的一个泛函,带约束的极值,引入拉格朗日乘数法
整理得到
然后带入上面的约束
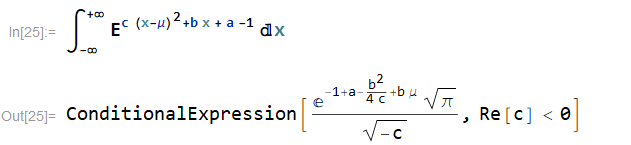
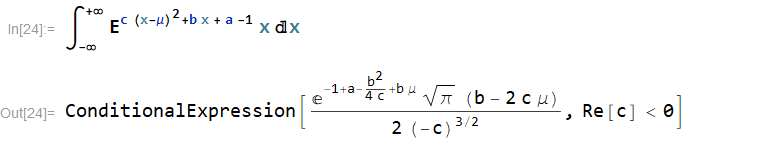
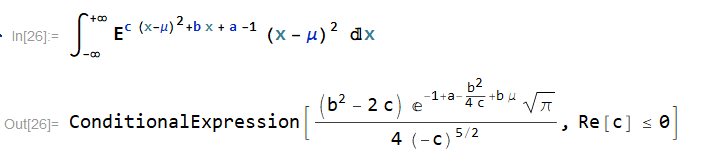
最后再借助求解方程组

得到
带入上面的方程得
泛函求导
泛函求导下次再补充
可以参照:泛函求导
