@zsh-o
2018-06-25T15:26:44.000000Z
字数 2252
阅读 4385
二项式分布 与 beta分布 关系的等式
机器学习
《LDA数学八卦》中关于Beta分布的解释特别漂亮,在这里整理记录一下
二项式分布
做次伯努利实验,成功的概率为,设成功的次数为,
组合数是,有区别的基本实验,成功k次的等价事件个数
Beta分布
1:
2: 把这个随机变量排序后得到的顺序统计量
3: 求的分布
假设落在了区间,需要求如下的概率
则被分割成了三段
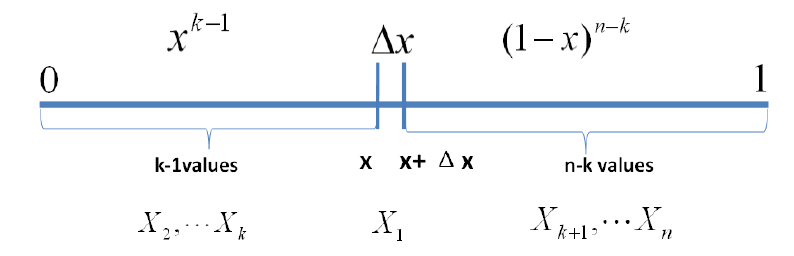
可以把基本事件设为
则
考虑排列组合,个数只有一个落在了有种取法,个数有个落在了有种取法,故与等价的事件的个数为
另外为了构造完整的概率表示,其考虑了多个点落在的情况
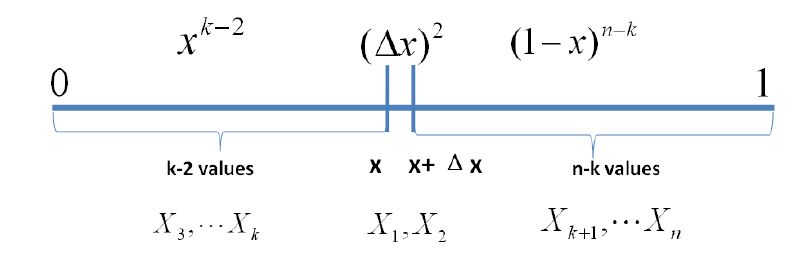
故,只要落在内的数字超过一个,则对应事件的概率就是,则有
故的概率密度可以表示为
二项式分布 与 beta分布 关系的等式
服从二项式分布,则其满足如下等式
这个式子很神奇,其把概率固定的二项式分布的累积分布函数的离散求和表示成了概率可变的积分的形式,但分布的随机变量就可以当做二项分布的概率,使其共轭,这也就能说的过去。这个式子可以依据上面的思路用一种等价的方式来说明
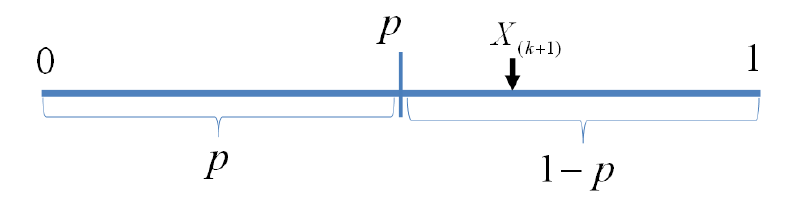
有随机变量,构造二项式分布,实验成功,用于成功的计数,于是构造了一个计数与概率等价的式子
等式左边表示贝努力实验成功次数最多次,右边表示第大的数对应于失败的贝努力实验,从而失败次数最少是次,所以左右两边等价
