前缀和数组 树形数组 线段树

算法

---

这是上上周学的知识点，但现在发现对树形数组的存储细节和节点访问时的下标计算有些忘了～忘了～～还是不贪快，多整理总结的好

这三种最终都可以理解成一颗树的形式，按照树的方式更能理解每一种表达方式面临的问题

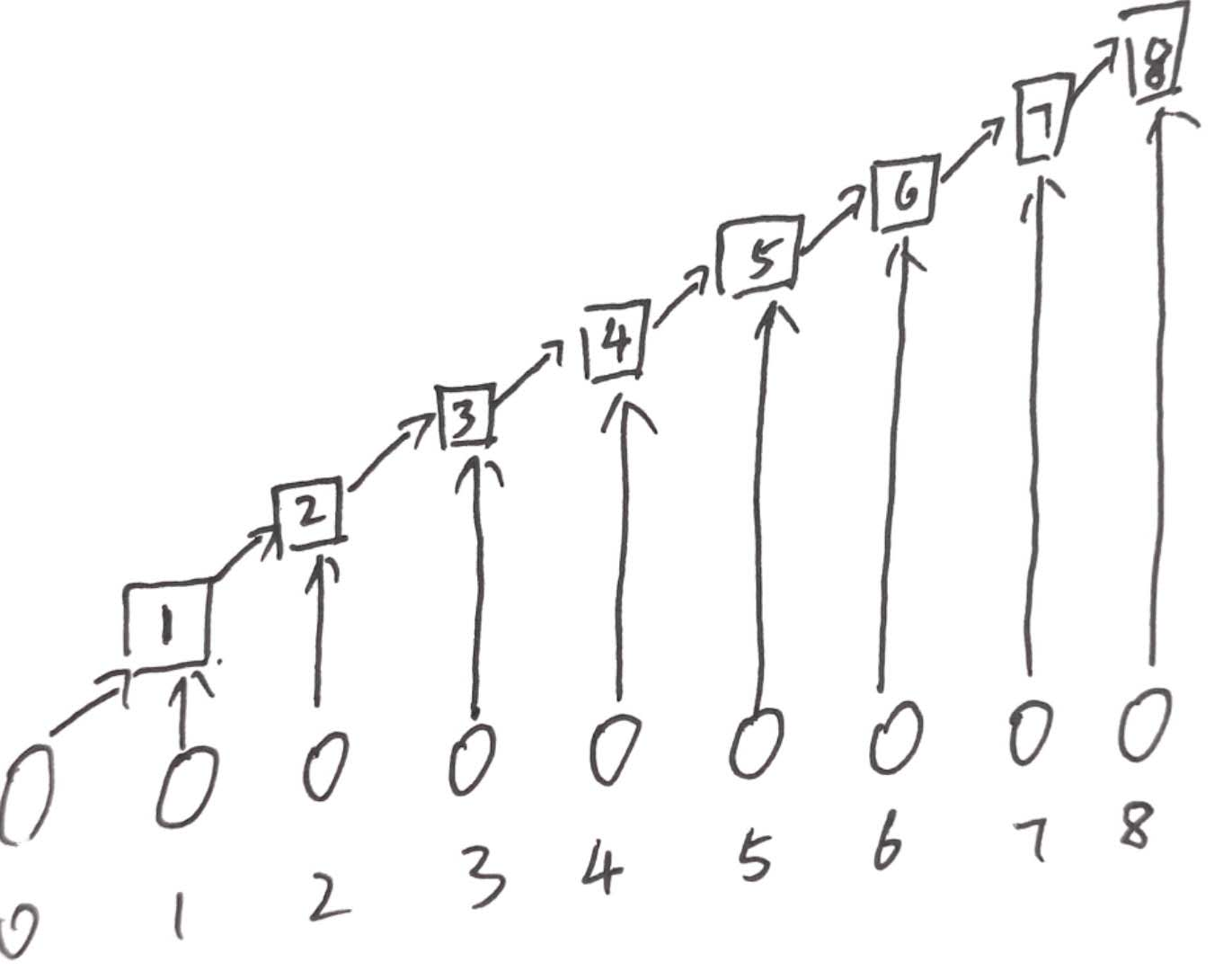
前缀和数组

用于求区间和，用于中间元素不修改的区间求和，如果修改中间元素AA[i]，则该元素对应的前缀和数组PSUM[i]及其后所有元素都需要刷新

数组	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
A[i]	0	2	6	3	10	4	3	11	7	4	9	8	2	1	5	6	3
PSUM[i]	0	2	8	11	21	25	28	39	46	50	59	67	69	70	75	81	84

$$\mathbf{PSUM}_i = \mathbf{PSUM}_{i-1} + \mathbf{A}_i$$

for(int i=1; i<=n; i++){
    PSUM[i] = PSUM[i-1] + A[i];
}

$$\mathbf{SUM}_{i,j} = \mathbf{PSUM}_j - \mathbf{PSUM}_{i-1}$$

for(int mi=0; mi<m; mi++){
    int a,b;
    cin>>a>>b;
    cout<<PSUM[max(a,b)]-PSUM[min(a,b)-1]<<endl;
}

树形数组

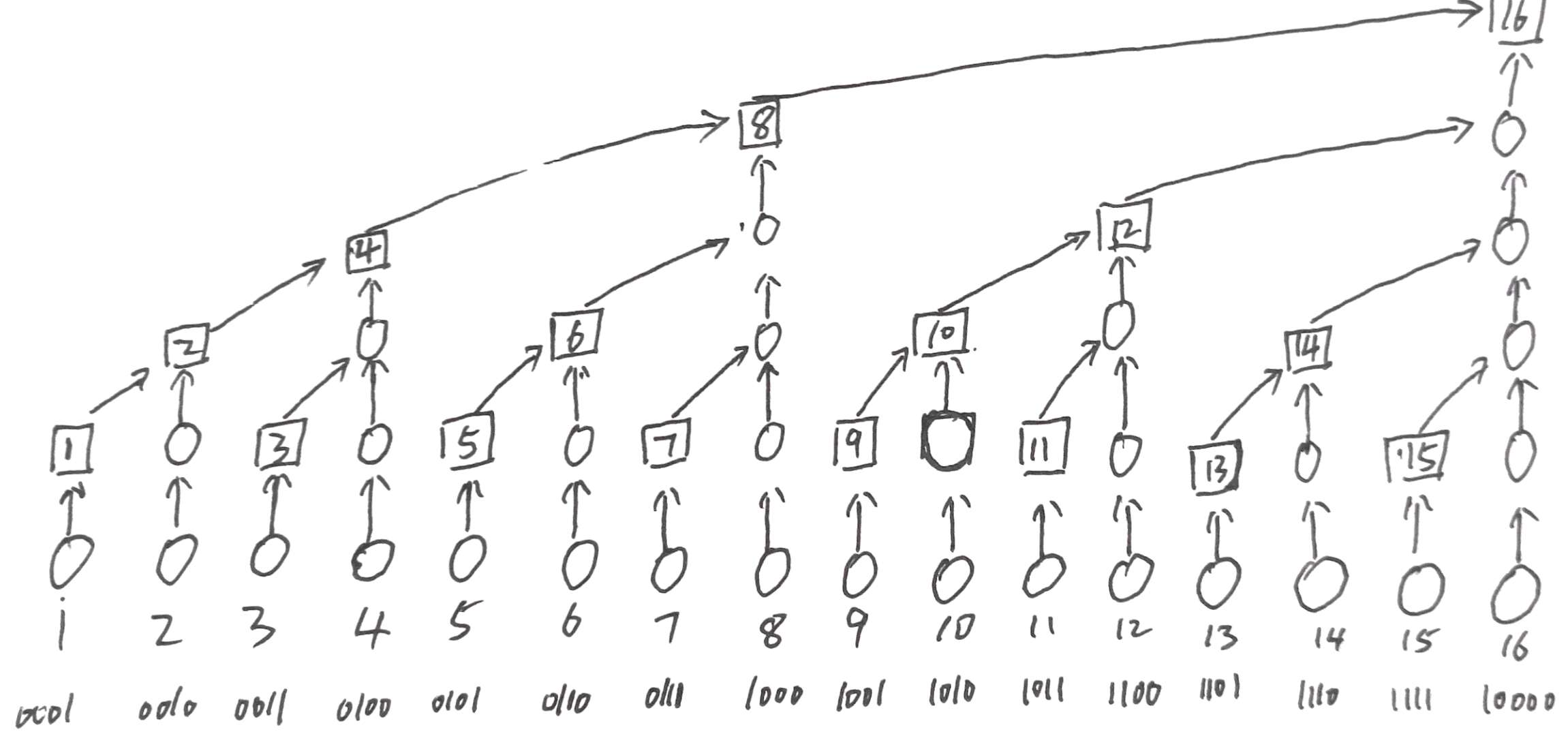
如上图所示树形数组的构造成了一种二叉树的形式，具体的思想是：现有$i$的二进制，其二进制末尾有$k$个0，那么树形数组的第$i$项就与原数组的前$2^k$个数有关，这里是求和，有神人把这个$i$和$2^k$用了一个特别简洁的式子给结合起来了

$$\mathbf{lowbit}(x) = x\&(-x)$$

int lowbit(int x){
    return x&(-x);
}

那么第i项的值与前lowbit(i)项有关，也就是说第$10$项的二进制是$1010$，lowbit(10) = 2，则BST[10] = A[9] + A[10]，并且修改A[10]，需要更新BST[10]、BST[12]、BST[16]，在总结点是$16$的情况下
然而，如果要计算前$10$项的和的话，我们知道BST[10]只是为第$9$、$10$的和，我们还需要前8项的和，而BST[8]正好是前$8$项的和，而且$8=10-lowbit(10)$，这样正好构成了一个循环

这里最巧妙的就是根据第i项的i的二进制编码，把原数据用二叉树的形式组织起来了

这样初始化树形数组需要借助于前缀和数组

for(int i=1; i<=CTSIZE; i++){
    BST[i] = PRE[i] - PRE[i-lowbit(i)];
}

计算前$i$项的和是一个递归或者循环

int sum(int idx){
    int total = 0;
    while(idx>0){
        total += BST[idx];
        idx -= lowbit(idx);
    }
    return total;
}

如果需要改变第$i$项的值，也是需要借助于$lowbit(x)$函数，这个函数设计的真实巧妙

//idx增加val
void update(int idx, int val){
    while(idx <= CTSIZE){
        BST[idx] += val;
        idx += lowbit(idx);
    }
}

最后如果要计算$i$到$j$项的和需要做一次差

sum(j) - sum(i-1)

线段树

线段树又叫区间树，顾名思义，其很容易求解区间问题，树形数组不容易求解区间问题，以至于在求区间和的时候用的是两个大区间相减的做法，但遇到求什么区间最值呀，就不行了
而且树形数组的节点修改的时间复杂度是$O(\log(N))$，如果要修改一个区间中的所有值的话，树形数组需要一个一个的改，时间复杂度为$O(M\log(N))$

而线段树把区间表示成了一个完全二叉树，这里像树形数组一样，为了能够完全用数组来表示，而且能够用下标来提取相应元素，我们需要首先把节点扩成$2$的幂次的形式

//把N扩充为2的幂
int t = 1;
while(t<N)
    t = t<<1;
N = t;

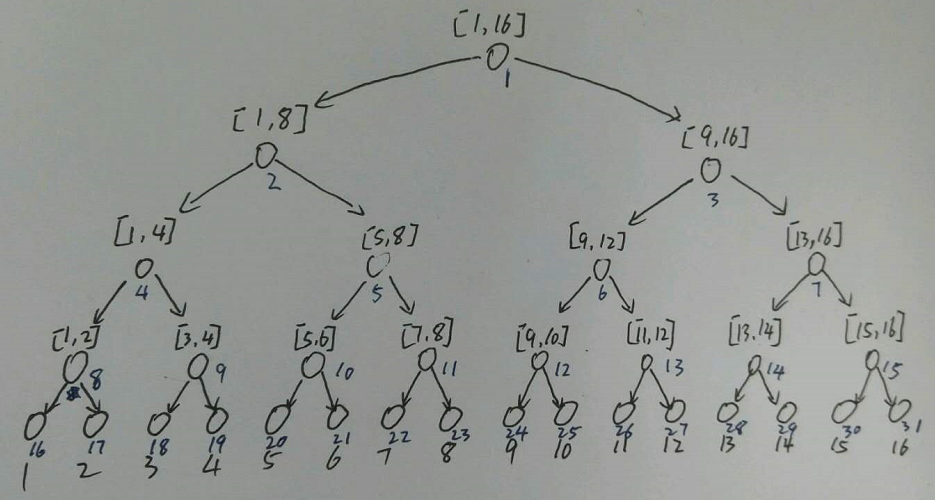
上图中，蓝色中性笔代表节点在数组中的位置，从上图可以看出来，我们用二分法的方法把每个二分区间表示了出来，这样其相应的关系也出来了，由于我们事先扩展成了$2$的幂次，故，该树一共有$1+\log N$层，总节点个数为$2^{1+\log N}-1 = 2\cdot 2^{\log N}-1 = 2N-1$，，非叶子节点也即区间个数为$N-1$，叶子节点个数为$N$

那么线段树的数组的第$N$到$2N-1$项为原始数组的值

//叶子节点位置：[N, 2N-1]
for(int i=0; i<N; i++){
    Tree[N+i] = A[i];
}

从图也可以看出，第$i$个节点的左右子树的下标正好是$2i$和$2i+1$，也可以写成i<<1和i<<1|1，因此用$O(N)$即可完成线段树初始化

//第i个节点左右子树的位置为[2*i, 2*i+1]=> [i<<1, i<<1|1]
//Tree从1开始
for(int i=N-1; i>=1; i--){
    Tree[i] = min(Tree[i<<1], Tree[i<<1|1]);
}

这时如果要改变一个单一的节点，只需要按照树修改相应的结构即可，其实也就是一直除以$2$

void change(int id, int value){
    int tid = N+id-1; //该节点Tree数组中的位置
    Tree[tid] = value;
    while(tid>1){
        tid = tid>>1;
        Tree[tid] = min(Tree[tid<<1], Tree[tid<<1|1]); //这里是求最小值
    }
}

线段树可以完成区间查询，区间查询使用一个递归遍历该树，然后后序遍历返回值即可

//[i,j]要查询的区间，[p,q]当前节点表示的区间，id当前节点下标
int query(int i, int j, int p, int q, int id){
    if(i<=p && j>=q){
        return Tree[id];
    }
    if(p>j || q<i){
        return INT_MAX;
    }
    //左移可以使用id<<1|1，右移相当于/2不可以这样用，只能((p+q)>>1)+1
    int a1 = query(i, j, p, (p+q)>>1, id<<1);
    int a2 = query(i, j, ((p+q)>>1)+1, q, id<<1|1);
    return min(a1, a2);
}

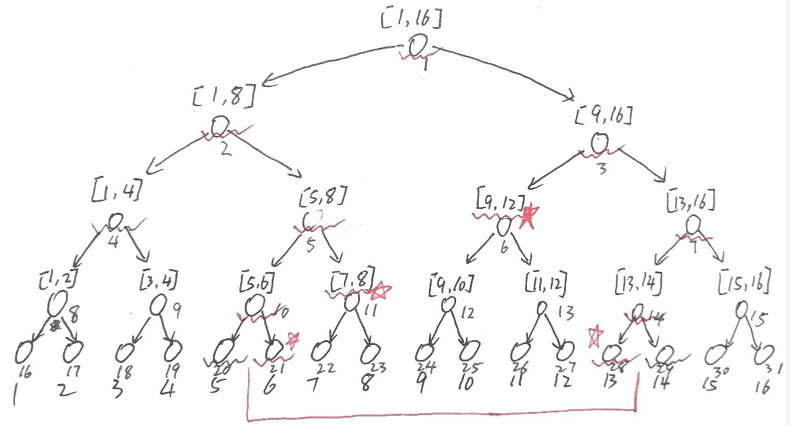
例如，这里要查询区间$[6,13]$，所有的波浪线为遍历到的节点，红波浪线不加星的表示要查询的区间与当前区间是交叉的，由此还要进行分裂查询；而红波浪线带红星的表示当前区间在要查询区间内部(i<=p && j>=q)，直接返回当前数组中的值即可；黑色波浪线表示要查询的区间与当前区间不相关(p>j || q<i)，需要返回一个无关的值，这里求得是最小值，所以返回的是极大值INT_MAX

有时候我们的问题是要修改一个区间中所有的值，例如，我们要把区间$[6,13]$全部换成一个值，如上面所说，一个一个换时间复杂度是$O(M\log N)$，我们要想办法把其优化到$O(\log N)$。如果用上面区间查询的方法修改区间值，那么该查询区间所有相关的区间均要修改，也就是说在区间查询中$6$和$11$节点由于完全在查询区间里面而且自身就是各自子节点的统计，所以不必再遍历其子节点，而区间修改需要用后续遍历的方式改变非叶子节点的统计值，所以$6$和$11$的子节点也需要遍历，因此时间复杂度为$O(N)$

为了能够达到$O(\log N)$，大哥们是这样考虑的，我们做区间修改的时候不改变中间区间的值，也即不改变6和11的值，反正其子节点的值都要改成同一个值，因此当前节点得值是区间长度X要改变的值，并增加一个“脏”标志位，表示该节点已经做了更改但其子节点未更改，然后下一次访问到该节点的时候，再把脏标志传递给左右两个子节点，这样段的修改和查询变为

int seg_change(int i, int j, int p, int q, int value, int id){
    if(i<=p && j>=q){
        Lazys[id] = value;
        //这里只是简单的把区间内的数全部设定同一个值
        Tree[id] = value * (q-p+1);
        return Tree[id];
    }
    if(p>j || q<i){
        return Tree[id];
    }
    if(Lazys[id]!=-1){
        Lazys[id<<1] = Lazys[id];
        Tree[id<<1] = ((q-p+1)>>1) * Lazys[id];
        Lazys[id<<1|1] = Lazys[id];
        Tree[id<<1|1] = ((q-p+1)>>1) * Lazys[id];
        Lazys[id] = -1;
    }
    int a = seg_change(i, j, p, (p+q)>>1, value, id<<1);
    int b = seg_change(i, j, ((p+q)>>1)+1, q, value, id<<1|1);
    //后序遍历刷新和
    Tree[id] = a+b;
    return Tree[id];
}
//[i,j]要查询的区间，[p,q]当前节点表示的区间，id当前节点下标
int query(int i, int j, int p, int q, int id){
    if(i<=p && j>=q){
        return Tree[id];
    }
    //求和，不在查询区间内的返回0
    if(p>j || q<i){
        return 0;
    }
    if(Lazys[id]!=-1){
        Lazys[id<<1] = Lazys[id];
        Tree[id<<1] = ((q-p+1)>>1) * Lazys[id];
        Lazys[id<<1|1] = Lazys[id];
        Tree[id<<1|1] = ((q-p+1)>>1) * Lazys[id];
        Lazys[id] = -1;
    }
    //左移可以使用id<<1|1，右移相当于/2不可以这样用，只能((p+q)>>1)+1
    int a1 = query(i, j, p, (p+q)>>1, id<<1);
    int a2 = query(i, j, ((p+q)>>1)+1, q, id<<1|1);
    return a1 + a2;
}