KMP

算法

KMP的next数组表示的是 当前字符匹配失败，应该跳转到模式串中哪个位置继续进行匹配，其本质思想是找到模式串当前位置的子串的前缀子串和后缀子串相同的最大长度$l$，这样匹配到当前位置不同时，原串中该位置前面$l$个字符仍与模式串中的前$l$个字符相同，故只需从$l+1$继续匹配即可

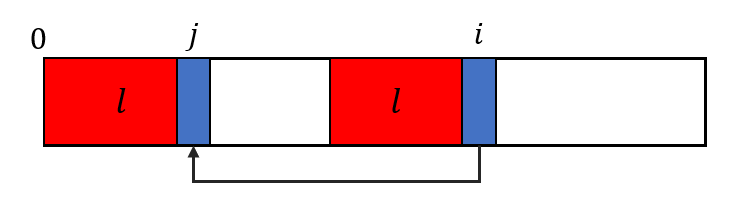
这是当前$i$位置所表示的情况，此时，next[i] = j，由于下标从0开始所以此时的相同串为红色部分并且长度为$l = j$，表示当i位置不同时需要继续匹配j位置的字符，那么需要分为两种情况：

• A[i] = A[j]：这时ij字符相同，那么前面红色部分的相同串就变成了$l+1$个，则next[i+1] = j+1
• A[i] != A[j]：这时ij字符不同，但下一个状态i+1需要满足前面next[i+1]个字符与[0, next[i+1]]相同，故这时需要A[i]==A[j]，故需要向前寻找j让A[i]==A[j]，并且满足$A[0,\cdots,j-1]==A[i-j, i-1]$，正好用next[j]来寻找

故生成next数组的代码为

int* get_next(char* A, int size_a){
    int* next = new int[size_a];
    A[0] = -1;
    A[1] = 0;
    int i = 0, j = 0;
    while(i < size_a){
        j = next[i - 1];
        while(j >= 0 && A[i-1] != A[j]){
            j = next[j];
        }
        next[i] = j + 1;
        i++;
    }
    return next;
}

匹配的代码与生成next数组的代码很相似，也很简单，这里返回第一次匹配成功的位置，没有则返回-1

int kmp_search(char* S, int size_s, char* A, int size_a, int* next){
    int index = -1;
    int i = 0, j = 0;
    while(i < size_s){
        while(j >= 0 && S[i] != A[j]){
            j = next[j];
        }
        j++;
        i++;
        if(j == size_a){
            index = i - j;
            break;
        }
    }
    return index;
}

这里有一点需要注意，以前需要的一个题，用kmp寻找模式串在原串中出现的次数，这时next数组只需要添加最后一位匹配成功后应该转移的位置即可，只需要修改匹配完成部分的代码即可

int* get_next_statistic(char* A, int size_a){
    int* next = new int[size_a + 1]; // *
    A[0] = -1;
    A[1] = 0;
    int i = 0, j = 0;
    while(i <= size_a){ // *
        j = next[i - 1];
        while(j >= 0 && A[i-1] != A[j]){
            j = next[j];
        }
        next[i] = j + 1;
        i++;
    }
    return next;
}
int kmp_search_statistic(char* S, int size_s, char* A, int size_a, int* next){
    int r = 0;
    int i = 0, j = 0;
    while(i < size_s){
        while(j >= 0 && S[i] != A[j]){
            j = next[j];
        }
        j++;
        i++;
        if(j == size_a){
            r++;
            j = next[j];
        }
    }
    return r;
}

结果：

int main(){
    char* S = "abababaabcacabaabcacab";
    char* A = "abaabcacab";
    printf("%d\n",kmp_search(S, strlen(S), A, strlen(A), get_next(A, strlen(A))));
    printf("%d\n",kmp_statistic(S, strlen(S), A, strlen(A), get_next_statistic(A, strlen(A))));
}

4
2