ST RMQ 区间最值 hihoCoder 1068 1710

算法 hihoCoder

---

用以求解区间最值，原理是DP，但单纯用DP的话，构建表的过程的时间复杂度为$O(N^2)$，为了压缩建表的时间复杂度，大哥们根据二分策略把时间复杂度降到$O(N\log N)$

F[i,j]：从第$i$个数开始的$2^j$个数满足的极值数（最小值，最大值，或者某种计数），这样就把区间$[i,j]$分成了等长的两部分$[i,i+2^{j-1}-1]$和$[i+2^{j-1},i+2^j-1]$，因此迭代公式为

$$F[i,j] = \max(F[i, j-1], F[i+2^{j-1},j-1])$$
F[i][0]为初始化的原值，长度为$2^0=1$：

scanf("%d", &N);
for(int i=1; i<=N; i++){
    scanf("%d", &F[i][0]);
}

int log2(int x){
    int n = 0;
    while((1<<n)<=x){
        n++;
    }
    return n-1;
}
void init(){
    int length = log2(N);
    for(int j=1; j<=length; j++){
        for(int i=1; i<=N-(1<<j)+1; i++){
            F[i][j] = min(F[i][j-1], F[i+(1<<(j-1))][j-1]);
        }
    }
}

我们要查询$[a, b]$，但dp表中代表的长度均为2的幂，故，采取的方法为把要查询的区间分为两部分，每一部分长度均为$2$的幂，最后返回两者的较小值，该长度计算公式为log2(b-a+1)

int query(int i, int j){
    int k = log2(j-i+1);
    return min(F[i][k], F[j-(1<<k)+1][k]);
}

hihoCoder 1710

题意

给定N个整数$A_1, A_2, \cdots, A_N$，小Hi会询问你M个问题。

对于每个问题小Hi给出两个整数$L$和$R$($L$ ≤ $R$)，请你找出$[A_L, A_{L+1}, A_{L+2}, ... A_R]$中最长的等差连续子数列，并输出其长度。

例如[2, 3, 5, 7, 9]中最长的等差连续子数列是[3, 5, 7, 9]长度为4。

分析

当时做的时候看错题了，没有注意其要求是等差连续子序列，下面分析，有和没有这个条件的解法

有连续条件的限制之后问题变得很简单，首先算出差值数组$\mathrm{SUB}$

$$\mathrm{SUB}_i = A_i - A_{i-1}$$
因为是连续的，再建一个数组保存SUB中相同串的长度

scanf("%d %d", &N, &M);
for(int i=1; i<=N; i++){
    scanf("%d", &A[i]);
}
SUB[1] = INT_MAX;
NUMM[1] = 1;
for(int i=2; i<=N; i++){
    SUB[i] = A[i] - A[i-1];
    NUMM[i] = SUB[i]==SUB[i-1]? NUMM[i-1]+1 : 2;
}

给定区间$[a,b]$用NUMM数组计算区间内等差连续子序列的长度

先介绍一种最容易想的方法：直接算。。。

int query(int a, int b){
    int t = b;
    int result = 0;
    while(a<t){
        t = b - NUMM[b] + 1;
        if(NUMM[b]>result){
            if(t<a){
                result = max(b - a + 1, result); //防止当前的最大值发生在边界
            }else{
                result = NUMM[b];
            }
        }
        b = t;
    }
    return result;
}

另一种利用RMQ，只不过，RMQ中保存的是区间中最大数的下标，因为有三种情况，假设查询的区间为$[a,b]$，最长等差连续子序列可能满足三种情况

根据NUMM数组寻找区间最大值下标

void init(){
    for(int i=1; i<=N; i++){
        F[i][0] = i;
    }
    int t = log2(N);
    for(int j=1; j<=t; j++){
        for(int i=1; i<=N-(1<<j)+1; i++){
            int a1 = F[i][j-1];
            int a2 = F[i+(1<<(j-1))][j-1];
            F[i][j] = NUMM[a1] >= NUMM[a2]? a1 : a2;
        }
    }
}
int query(int a, int b){
    int t = log2(b-a+1);
    int a1 = F[a][t];
    int a2 = F[b-(1<<t)+1][t];
    return NUMM[a1] >= NUMM[a2]? a1 : a2;
}

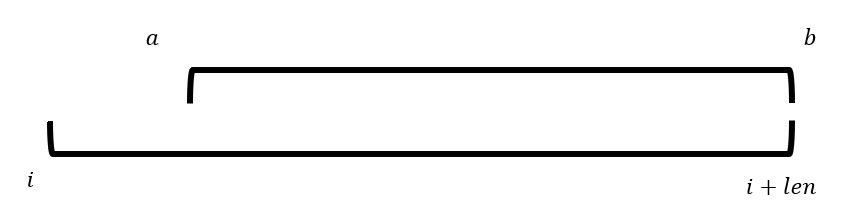
情况一，该串正好完全在区间内部，这时所求的长度就是$len$

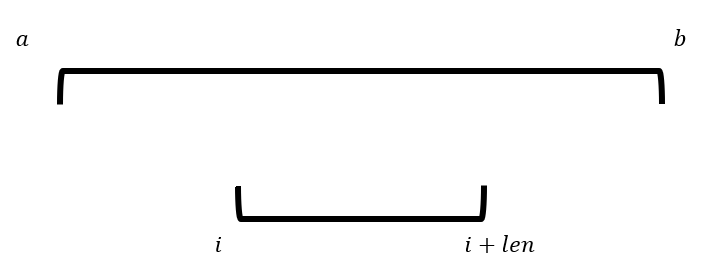
情况二，该串与区间左相交，这时该串满足条件的长度只是相交部分要小于$len$，所以这时要求右边不想交部分的最大值，再与相交部分长度比较

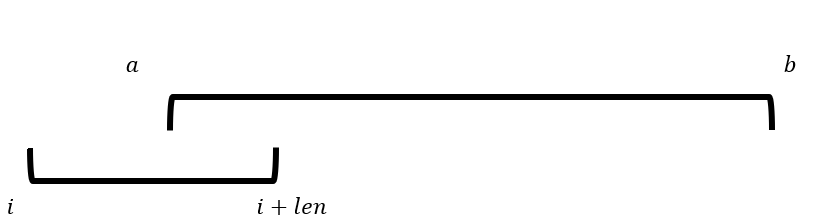
第三种更独特的情况是，左相交，并且有边界与$b$重合，这时所求长度就是区间长度$b-a+1$

int a, b;
for(int i=0; i<M; i++){
    scanf("%d %d", &a, &b);
    int idx = query(a, b);
    if(a <= idx - NUMM[idx] +1)
        printf("%d\n", NUMM[idx]);
    else{
        int t = idx - a + 1;
        if(idx == b)
            printf("%d\n", t);
        else
            printf("%d\n", max(t, NUMM[query(idx+1, b)]));
    }
}