Expectation Maximisation (EM)

机器学习

---

最近在看混合模型，但发现最基本的EM都没有真正学懂，看Richard的课件很有启发，整理一下，主要是高斯混合模型下的EM的公式推导和收敛证明

单高斯分布的极大似然估计(Maximum Likelihood Estimation)

假设数据是由单个高斯分布产生的 $x\sim \mathcal{N}(\mu,\Sigma)$，我们有观测值 $x_i\in\mathcal{D}$，需要根据这些观测值估计出高斯分布的参数 $\mu$ 和 $\Sigma$，由于单个高斯很简单，只需要最大化似然概率即可

$$\begin{align*} \log p(\textit{X}) & =\sum_{i=1}^N \log \mathcal{N}(x_i \mid \mu, \Sigma) \\ & = \sum_{i=1}^N \log \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x_i-\mu)^2}{2\sigma^2}} \\ & = \sum_{i=1}^N\log \frac{1}{\sqrt{2\pi}\sigma} + \sum_{i=1}^N - \frac{(x_i-\mu)^2}{2\sigma^2} \\ & = -\frac{N}{2}\log 2\pi - \frac{N}{2}\log \sigma^2 - \frac{1}{2\sigma^2}\sum_{i=1}^N (x_i-\mu)^2 \end{align*}$$

$$\begin{align*} \frac{\partial \log p(\textit{X})}{\partial \mu}& = \frac{1}{\sigma^2}\sum_{i=1}^N (x_i-\mu)=0\\ & \Rightarrow \mu = \frac{1}{N}\sum_{i=1}^N x_i \\ \frac{\partial\log p(\textit{X})}{\partial\sigma^2} & = -\frac{N}{2\sigma^2} + \frac{1}{2\sigma^4}\sum_{i=1}^N(x_i-\mu)^2=0 \\ & \Rightarrow \sigma^2 = \frac{1}{N}\sum_{i=1}^N (x_i-\mu)^2 \end{align*}$$

高斯混合模型(Gaussian Mixture Model)

概率模型是对观测数据概率的估计，混合模型采用多个分布线性组合的方法来估计数据的真实分布，K个高斯概率密度的叠加

$$p(x) = \sum_{k=1}^K \pi_k\mathcal{N}(x\mid \mu_k,\Sigma_k)\\ \begin{align*} s.t. & \sum_{k=1}^K \pi_k=1\\ & 0 \leq \pi_k\leq 1 \end{align*}$$

如果把 $\pi_k$ 看作是每个$component$出现的概率 $p(k)$，那么模型等价于一个条件概率，那么生成$x$的路径需要经过两个步骤，首先从概率 $p(k)$ 得到一个分布，然后再在这个分布中得到 $x$ ，那么其边缘概率密度为

$$p(x)=\sum_{k=1}^K p(k)p(x \mid k)$$

虽然在路径上其最终是由单个分布产生的，但其在整个分布上来说是由多个基本分布线性叠加的（求期望，把$component$积分掉）, 那么$component$的后验分布 $p(k\mid x)$ 表示观测$x$属于每一个$component$的概率, 是一个离散概率 $x\sim Discrete(\pi_1, \cdots, \pi_k)$, 根据贝叶斯公式得

$$\begin{align*} p(k\mid x) & = \frac{p(x\mid k)p(k)}{\sum_l p(x\mid l)p(l)} \\ & = \frac{\pi_k \mathcal{N}(x \mid \mu_k, \Sigma_k)}{\sum_l \pi_l \mathcal{N}(x \mid \mu_l, \Sigma_l)} \end{align*}$$

其对数似然为

$$\begin{align*} \log p(X) & = \sum_{i=1}^N \log \left\{ \sum_{k=1}^K \pi_k \mathcal{N}(x_i \mid \mu_k, \Sigma_k) \right\} \end{align*}$$

由于对数里面有一个求和式, $MLE$的方法太复杂

引入隐变量$z_i$, z服从多项式分布, 表示有k个状态, 每次以一定的概率从这些状态中选择一个, 代表第$i$个观测值$x_i$是从第$z_i$个分布产生的, 则$GMM$可以表示成

$$\begin{align*} z_i & \sim Multinoimal(\pi_1, \cdots, \pi_k) \\ x_i \mid z_i & \sim \mathcal{N}(\mu_{z_i},\Sigma_{z_i}) \end{align*}$$

EM

$EM$用以迭代的方法估计具有隐变量的概率模型, 思想是
- E-step: 在现有 $\theta^{(t)}$ 下最大化似然下界, 计算隐变量 $z$ 的期望 $Q(z_i)=p(z_i\mid x_i,\theta)$ 作为其下界
- M-step: 在上面 $Q(z_i)$ 下计算参数列表 $\theta$ 来最大化似然

Jensen不等式

$f$为凸函数, $\forall_{x\in \mathbb{R}}, f''(x)\geq 0$, 当$x$为向量，如果其hessian矩阵H是半正定的($H\geq 0$)。如果$f''(x)>0$或者$H>0$, $f$是严格凸函数

Jessen不等式: 如果$f$是凸函数, $E[f(X)]\geq f(E[X])$。当且仅当 $x$ 是常量 $c$ 的时候, $E[f(x)] = f(E[x])$

EM推导

引入隐变量z之后的对数似然函数为

$$\begin{align*} \mathcal{L}(\theta;X) & = \sum_{i=1}^N\log p(x_i \mid \theta) \\ & = \sum_{i=1}^N\log\sum_{z_i}p(x_i,z_i \mid \theta) \\ & = \sum_{i=1}^N \log \sum_{z_i}Q(z_i)\frac{p(x_i,z_i\mid \theta)}{Q(z_i)} \\ & \geq \sum_{i=1}^N \sum_{z_i} Q(z_i)\log\frac{p(x_i,z_i\mid \theta)}{Q(z_i)} \end{align*}$$

这里定义$Q(z_i)$是关于$z_i$的函数, 并且 $\sum_{z_i}Q(z_i)=1$, 函数的期望 $E_{x\sim p}[g(X)]=\sum_xg(x)p(x)$, 那么对于上式来说, $p(x)$ 对应 $Q(z_i)$ 表示 $z_i$ 的概率, $g(x)$ 对应 $\log\frac{p(x_i,z_i\mid \theta)}{Q(z_i)}$ 表示 $z_i$ 的函数,而且$\log$为凹函数, 最后根据Jensen不等式

$$f\begin{pmatrix} E_{z_i\sim Q} \begin{bmatrix} \frac{p(x_i,z_i\mid \theta)}{Q(z_i)} \end{bmatrix}\end{pmatrix} \geq E_{z_i\sim Q} \begin{bmatrix} f\begin{pmatrix} \frac{p(x_i,z_i\mid \theta)}{Q(z_i)} \end{pmatrix} \end{bmatrix}$$

在这里我们要最大化这个似然函数的下界，也即是使函数 $g(x)$ 为常数 $c$

$$\frac{p(x_i,z_i\mid \theta)}{Q(z_i)}=c$$

对公式进行变换,

$$\begin{align*} p(x_i,z_i\mid \theta) & = c\cdot Q(z_i) \\ \sum_{z_i}p(x_i,z_i\mid \theta) & = c \cdot \sum_{z_i} Q(z_i) \\ c & = \sum_{z_i}p(x_i,z_i\mid \theta) \\ Q(z_i) & = \frac{p(x_i,z_i\mid \theta)}{\sum_{z_i}p(x_i,z_i\mid \theta)} \\ & = p(z_i \mid x_i, \theta) \end{align*}$$

执行完上面E-step之后下界重合, 这时取等号, 似然变为

$$\mathcal{L}(\theta^{(t)};X) = \sum_{i=1}^N \sum_{z_i} Q^{(t)}(z_i)\log\frac{p(x_i,z_i\mid \theta^{(t)})}{Q^{(t)}(z_i)}$$

现在要对公式求导再等于0求方程得到最优的参数列表

$$\theta^{(t+1)} = \underset{\theta}{\arg\max}\mathcal{L}(\theta;X)$$

这时得到 $t+1$ 步的似然函数 $\mathcal{L}(\theta^{(t+1)};X)$, 现在要证明EM的收敛性只需要证明 $\mathcal{L}(\theta^{(t+1)};X) \geq \mathcal{L}(\theta^{(t)};X)$ ,

$$\begin{align*} \mathcal{L}(\theta^{(t+1)};X) & = \sum_{i=1}^N \log \sum_{z_i}Q^{(t)}(z_i)\frac{p(x_i,z_i\mid \theta^{(t+1)})}{Q^{(t)}(z_i)} \\ & \geq \sum_{i=1}^N \sum_{z_i} Q^{(t)}(z_i)\log\frac{p(x_i,z_i\mid \theta^{(t+1)})}{Q^{(t)}(z_i)} \\ & \geq \sum_{i=1}^N \sum_{z_i} Q^{(t)}(z_i)\log\frac{p(x_i,z_i\mid \theta^{(t)})}{Q^{(t)}(z_i)} \\ & = \mathcal{L}(\theta^{(t)};X) \end{align*}$$

GMM

E-step: $\theta^{(t)}$ 已知, 求此时的 $Q^{(t+1)}(z_i)$

$$\begin{align*} Q^{(t+1)}(z_i) & = \frac{p(x_i,z_i \mid \theta^{(t)})}{p(x_i \mid \theta^{(t)})} \\ & = \frac{p(x_i,z_i \mid \theta^{(t)})}{\sum_{l\in z_i}p(x_i,l \mid \theta^{(t)})} \\ & = \frac{p(x_i \mid z_i, \theta^{(t)})p(z_i \mid \theta^{(t)})}{\sum_{l \in z_i}p(x_i \mid l, \theta^{(t)})p(l \mid \theta^{(t)})} \\ & = \frac{\mathcal{N}(\mu_{z_i},\Sigma_{z_i})\pi_{z_i}}{\sum_{l\in z_i}\mathcal{N}(\mu_l,\Sigma_l)\pi_l} \end{align*}$$

M-step: $Q^{(t+1)}$ 已知，求此时的 $\theta^{(t+1)}$

$$\begin{align*} \mathcal{L}(\theta;X) & = \sum_{i}^N\sum_l^K Q_i(l)\log\frac{p(x_i,l \mid \theta)}{Q_i(l)} \\ & = \sum_{i}^N\sum_l^K Q_i(l)\log p(x_i,l\mid \theta) - \sum_{i}^N\sum_l^K Q_i(l)\log Q_i(l) \\ & = \sum_{i}^N\sum_l^K Q_i(l)\log p(x_i,l\mid \theta) - Constant \\ & = \sum_{i}^N\sum_l^K Q_i(l)\log \pi_l \mathcal{N}(\mu_l,\Sigma_l) - Constant \\ & = \sum_{i}^N\sum_l^K Q_i(l)\log\pi_l + \sum_{i}^N\sum_l^K Q_i(l)\log\mathcal{N}(\mu_l,\Sigma_l) - Constant \end{align*}$$

计算 $\pi$:

$$\begin{align*} \forall_{l\in\{1,\cdots,K\}}, & \frac{\partial\mathcal{L}(\theta;X)}{\partial\pi_l}=0 \\ & s.t. \sum_l^K \pi_l=1 \end{align*}$$

利用拉格朗日乘数法添加约束项

$$\left\{\begin{align*} L_{\pi_l} &= \frac{\partial\mathcal{L}(\theta;X)}{\partial\pi_l} + \lambda (\sum_l^K \pi_l-1) =0 \\ L_\lambda &= \sum_l^K \pi_l-1 = 0 \end{align*}\right.$$

求导得

$$\left\{\begin{align*} \frac{1}{\pi_1}\sum_i^N Q_i(1) - \lambda & = 0 \\ \vdots \\ \frac{1}{\pi_l}\sum_i^N Q_i(l) - \lambda & = 0 \end{align*}\right.$$

对上式整理并相加得

$$\sum_l^K\sum_i^N Q_i(l) = \lambda \sum_l^K\pi_l=\lambda$$

由于

$$Q_i(l) = p(l\mid x_i,\theta)$$

得到

$$\begin{align*} \sum_l^K\sum_i^N Q_i(l) & = \sum_i^N\sum_l^K Q_i(l) \\ & = \sum_i^N\sum_l^K p(l\mid x_i,\theta) \\ & = \sum_i^N 1 \\ & = N \end{align*}$$

则，

$$\begin{align*} \pi_l & = \frac{1}{\lambda}\sum_i^N Q_i(l) \\ & = \frac{1}{N} \sum_i^N Q_i(l) \\ & = \frac{1}{N} \sum_i^N p(l\mid x_i,\theta) \end{align*}$$

计算 $\mu$:

$$\begin{align*} & \sum_{i}^N\sum_l^K Q_i(l)\log\mathcal{N}(\mu_l,\Sigma_l) \\ & = \sum_{i}^N\sum_l^K Q_i(l)\log \frac{1}{\sqrt{2\pi}\sigma_l}e^{-\frac{(x_i-\mu_l)^2}{2\sigma_l^2}} \\ & = \sum_{i}^N\sum_l^K Q_i(l)\left\{ -\frac{1}{2}\log2\pi - \frac{1}{2}\log \sigma_l^2 - \frac{(x_i-\mu_l)^2}{2\sigma_l^2} \right\} \\ \end{align*}$$

对 $\mu_l$ 求偏导得

$$\begin{align*} \frac{\partial \mathcal{L}(\theta;X)}{\partial \mu_l} & = \sum_{i}^N Q_i(l)\frac{x_i-\mu_l}{\sigma^2} \\ & = 0 \end{align*}$$

得

$$\mu_l=\frac{\sum_{i}^N Q_i(l)x_i}{\sum_{i}^N Q_i(l)}$$

计算 $\sigma$:

上面式子对 $\sigma^2_l$ 求偏导得

$$\begin{align*} \frac{\partial \mathcal{L}(\theta;X)}{\partial \sigma^2_l} & = \sum_{i}^N Q_i(l) \left\{ -\frac{1}{2\sigma_l^2} + \frac{(x_i-\mu_l)^2}{2\sigma_l^4} \right\} \\ & = 0 \end{align*}$$

得

$$\sigma_l=\frac{\sum_{i}^N Q_i(l)(x_i-\mu_l)^2}{\sum_{i}^N Q_i(l)}$$

由公式可以得到, $\mu_l$ 和 $\sigma_l$ 是通过 $Q_i(l)$ 对观测数据进行加权平均

从KL散度角度解释EM

KL散度角度是用 $q(z)$ 来估计 $z$ 的后验概率 $p(z \mid x,\theta)$, 则其KL散度为

$$\begin{align*} KL(q\parallel p) & = \sum_z q(z) \log\frac{q(z)}{p(z \mid x,\theta)} \\ & = \sum_z q(z) \log \frac{q(z)p(x\mid \theta)}{p(z,x \mid \theta)} \\ & = -\sum_z q(z) \log \frac{p(z,x \mid \theta)}{q(z)} + \sum_z q(z) \log p(x\mid \theta) \\ & = -\sum_z q(z) \log \frac{p(z,x \mid \theta)}{q(z)} + \log p(x\mid \theta) \sum_z q(z) \\ & = -\sum_z q(z) \log \frac{p(z,x \mid \theta)}{q(z)} + \log p(x\mid \theta) \end{align*}$$

$$\begin{align*} \log p(x\mid \theta) & = KL(q\parallel p) + \sum_z q(z) \log \frac{p(z,x \mid \theta)}{q(z)} \\ & = KL(q\parallel p) + \mathcal{L}(q,\theta) \end{align*}$$

这里 $\log p(x\mid \theta)$ 是上面说的对数似然, $KL(q\parallel p)$ 是kl散度, $\mathcal{L}(q,\theta)$ 在变分推理里面叫变分自由能, 是一个泛函, $KL(q\parallel p) \geq 0$ 当 $q(z)=p(z\mid x,\theta)$ 时等号成立

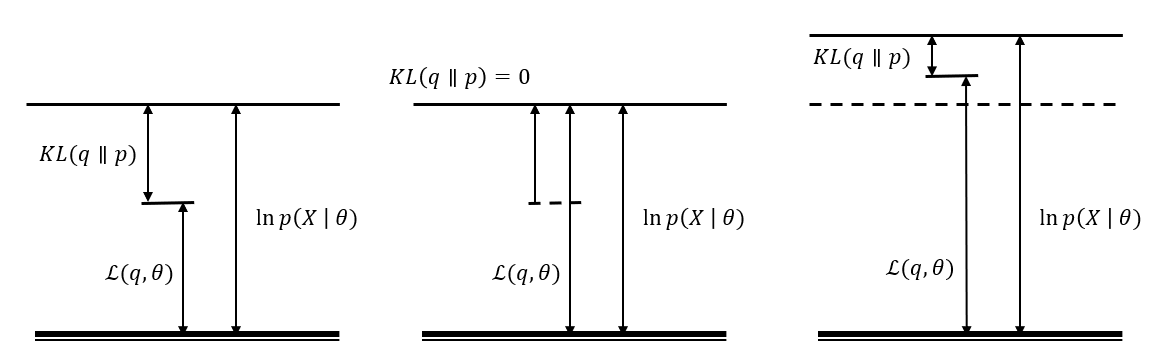
在EM的E步骤里此时的 $\theta^{(t)}$ 是已知的保持其固定, 我们通过最小化kl散度的下界也即 $q(z)=p(z\mid x,\theta)$, 使得 $\mathcal{L}(q,\theta)$ 达到其上界

在M步骤里, 保持 $q(z)=p(z\mid x,\theta)$ 求此时的 $\theta$ 使 $\mathcal{L}(q,\theta)$ 最大化, 这时三个值的上界都提高了

References

• PRML
• 徐亦达：EM
• EM-最大期望算法 by 刘帝伟