番外 - MCMC

机器学习 《统计学习方法》

---

%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt

蒙特卡洛 均值方法 求积分

利用一个容易进行抽样的分布，根据大数定理可以对函数积分进行估计

$$\begin{split} \int_a^b f(x)\mathrm{d}x & = \int_a^b p(x)\frac{f(x)}{p(x)}\mathrm{d}x \\ & = E_{p(x)}\Big[\frac{f(x)}{p(x)}\Big] \\ & = \frac{1}{N} \sum_{i=1}^N \frac{f(x_i)}{p(x_i)} \quad // x_i \sim p(x) \end{split}$$

def f(x):
    return 0.3 * np.exp(-(x - 0.3) ** 2) + 0.7 * np.exp(- (x - 2.) ** 2 / 0.3)

## 蒙特卡洛 均值法 求f的积分
def MC(f, low, high, size):
    z = np.random.uniform(low=low, high=high, size=size)
    return np.sum(f(z) * (high - low)) / size

Int_f = MC(f, -2, 4, 10**6)
Int_f

1.211298965791444

拒绝采样

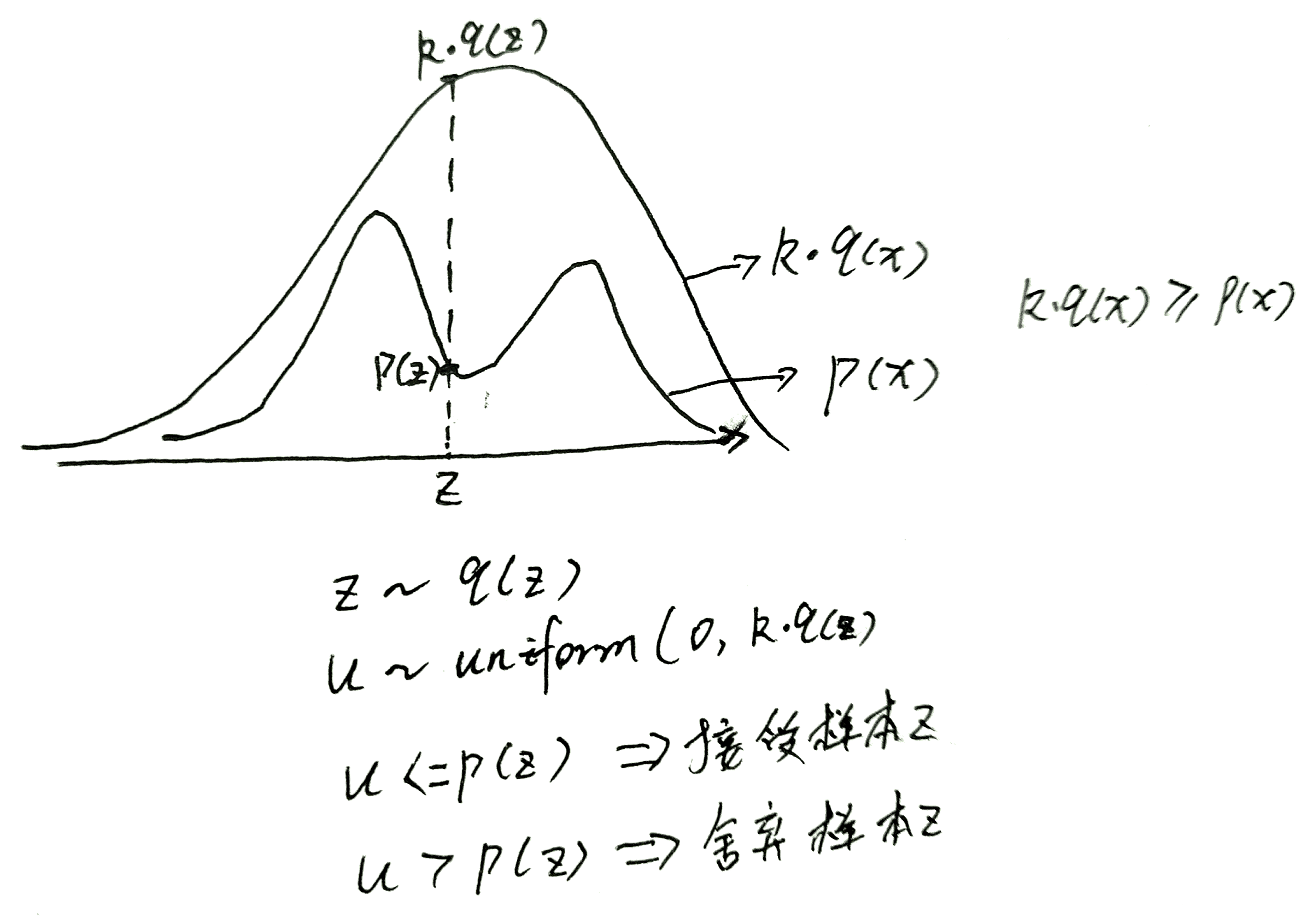
相当于在$kq(x)$所围成的区域里面进行抽样，只返回在$p(x)$所围成区域内部的采样点，这样在$kq(z)$所围成的区域进行抽样每个抽样点$z$的概率为$q(z)\cdot \frac{1}{kq(z)}=\frac{1}{k}$，$q(z)$表示$z$点处的概率，$\frac{1}{kq(z)}$表示上面的$u\sim uniform(0, kq(z))$表示在均匀分布进行采样，每个点的概率均是$\frac{1}{kq(z)}$，故这样得到的每个采样点的概率均相同并且等于$\frac{1}{k}$，相当于$kq(x)$的积分，然后根据蒙特卡洛思想，根据$p(z)$判断该点是否应该保留，则$z$被保留的概率为均匀分布$[0, kq(z)]$中的$[0, p(z)]$部分则保留概率为$\frac{p(z)}{kq(z)}$，然后再由$z$点的概率为$q(z)$，故经过该拒绝操作之后$z$点并且被接受的概率为

$$\begin{split} p(z, Acc=True) & =q(z) \cdot \frac{p(z)}{kq(z)} \\ & =\frac{p(z)}{k} \\ \end{split}$$

接受的概率为

$$\begin{split} p(Acc=True) & = \int_z p(z, Acc=True)\mathrm{d}z \\ & = \int_z \frac{p(z)}{k}\mathrm{d}z \\ & = \frac{1}{k} \end{split}$$

因此，总的迭代次数大致为所要样本点数的$k$倍
最后在接受的条件下每个点$z$的概率为

$$\begin{split} p(z\mid Acc=True) & = \frac{p(z, Acc=True)}{p(Acc=True)} \\ & = \frac{p(z)}{k}/\frac{1}{k} \\ & = p(z) \end{split}$$

size = 10**4
mean = 1.4
sigma = 1.2
k = 3

## 为了能够使后面的可视化对其曲线，对f(x)进行归一化，用的上面的均值方法
def p(x):
    return f(x) / Int_f
def q(x):
    return 1 / (sigma * np.sqrt(2 * np.pi)) * np.exp(- (x - mean) ** 2 / (2 * sigma ** 2))
def sample_q():
    return np.random.normal(loc=mean, scale=sigma)

def reject_sampling(p, q, sample_q, k, size):
    res = []
    it = 0
    ti = 0
    while(it < size):
        z = sample_q()
        qz = q(z)
        u = np.random.uniform(low=0,high=k*qz)
        pz = p(z)
        if u < pz:
            res.append(z)
            it += 1
        ti += 1
    return np.array(res), ti

sample, ti = reject_sampling(p, q, sample_q, k, size)
ti

30031

count, bins, ignored = plt.hist(sample, bins=300,density=True)
plt.plot(bins, p(bins))
plt.plot(bins, k * q(bins))

[<matplotlib.lines.Line2D at 0x15bbd3a0518>]

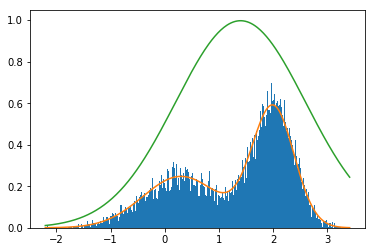
MCMC

这部分《LDA数学八卦》写的非常好了，这里只提一下
上面比较麻烦的是$k$的选择，如何消除$k$，MCMC的方法通过消除了$K$
MCMC用了马尔科夫的平稳分布的性质，无论初始概率分布$\pi_0$是多少，通过转移矩阵$P$的有限次状态转移后，最终都会收敛到平稳分布$\pi$，也即

$$\underset{n\rightarrow\infty}{\lim}P^n = \begin{bmatrix} \pi(1) & \cdots & \pi(j) & \cdots \\ \cdots & \cdots & \cdots & \cdots \\ \pi(1) & \cdots & \pi(j) & \cdots \\ \cdots & \cdots & \cdots & \cdots \end{bmatrix}$$

而且

$$\pi_j = \sum_i\pi_iP_{ij}\\ \pi P = \pi$$

此时有马氏链的状态转移过程表示如下，

$$X^{(0)} \sim p(x) \quad \xrightarrow{Sampling} x_0 \\ X^{(1)} \sim p(x\mid x_0) \quad \xrightarrow{Sampling} x_1 \\ \vdots \\ X^{(n)} \sim p(x\mid x_{n-1}) \quad \xrightarrow{Sampling} x_n \\ X^{(n+1)} \sim p(x\mid x_n) \quad \xrightarrow{Sampling} x_{n+1}\\ \vdots \\ $$

先只考虑$x_0$和$x_1$，由马氏链有$x_0$和$x_1$的联合概率为$p(x_0,x_1) = p(x_0)p(x_1\mid x_0)$，因而$x_1$的边缘概率为

$$\begin{split} p(x_1) & = p(X^{(1)} = x_1) \\ & = \sum_{x_0} p(X^{(0)} = x_0, X^{(1)} = x_1) \\ & = \sum_{x_0}p(x_0,x_1) \\ & = \sum_{x_0}p(x_0)p(x_1\mid x_0) \\ & = \sum_{x_0} \pi_{x_0}P_{x_0, x_1} \quad //\text{当初始状态为平稳分布$\pi$} \\ & = \pi_{x_1} \end{split}$$

由此$X_1\sim p(x) P$，当初始分布为平稳分布$\pi$时$X_1\sim \pi P = \pi$，故$X_0X_1$是独立同分布的，即使每一步均是从转移矩阵组成的概率里面进行抽样，抽样的边缘概率仍然满足平稳分布，也即每一个抽样点均满足抽样分布，而且当该过程持续到$X^{(n)}$，同理

$$p(x_0,x_1,\cdots,x_n) = p(x_0)p(x_1\mid x_0)\cdots p(x_n\mid x_{n-1}) \\ $$

$$\begin{split} p(x_n) & = \sum_{x_0,x_1,\cdots,x_{n-1}}p(x_0,x_1,\cdots,x_n) \\ & = \sum_{x_0,x_1,\cdots,x_{n-1}}p(x_0)p(x_1\mid x_0)\cdots p(x_n\mid x_{n-1}) \\ & = \sum_{x_0,x_1,\cdots,x_{n-1}} \pi_{x_0}P_{x_0,x_1}\cdots P_{x_{n-1},x_n} \\ & = \sum_{x_1,\cdots,x_{n-1}} \pi_{x_1}P_{x_1,x_2}\cdots P_{x_{n-1},x_n} \\ & \vdots \\ & = \sum_{x_{n-1}} \pi_{x_{n-1}} P_{x_{n-1}, x_n} \\ & = \pi_{n} \end{split}$$

故$X_n \sim p(x)P^n$，当初始为平稳分布时$X_n \sim \pi P^n = \pi$，故只需要有了平稳分布为要抽样分布的转移矩阵之后，就可以利用每次抽样状态转移的方法得到所要的抽样样本，而且即使初始分布不是平稳分布，由于任意初始分布经过有限步骤状态转移后均变成平稳分布，故抽样时可以是任意初始状态，在一定步骤之后就变成了所要的抽样

接下来问题变成了如何得到平稳分布是所要分布的转移矩阵，直接根据平稳分布构造转移矩阵是非常困难的，大哥们为平稳分布的转移矩阵添加了一个约束使其变得容易构造，该约束就是细致平稳条件

如果非周期马氏链的转移矩阵$P$和分布$\pi(x)$满足

$$\pi(i)P_{ij} = \pi(j)P_{ji} \qquad \text{for all $i,j$}$$ 则$\pi(x)$是马氏链的平稳分布，上式被称为细致平稳条件

满足细致平稳条件肯定是平稳分布

$$\sum_i \pi(i)P_{ij} = \sum_i\pi(j)P_{ji} = \pi(j) \sum_i P_{ji} = \pi(j) \\ \pi P = \pi$$

接下来是如何利用该细致平稳条件构造满足条件的转移矩阵，现有任意分布$p(i)$和任意转移矩阵$q(i,j)$，$ij$为状态，我们来构造

$$p(i)q(i,j)\alpha(i,j) = p(j)q(j,i)\alpha(j,i)$$ 使其满足细致平稳条件，很容易可以得到
$$\alpha(i,j) = p(j)q(j,i)\\ \alpha(j,i) = p(i)q(i,j)$$

此时的平稳分布即为$p(x)$转移矩阵为$Q_{ij} = q(i,j)\alpha(i,j) = q(i,j)p(j)q(j,i)$

再根据上面的抽样过程，当前状态为$i$，我们要从转移矩阵$Q(x\mid i)$中抽样得到下一个状态，相当于我们要在分布$Q(x\mid i)$中抽样，但该分布是不规则的无法直接抽样，但$q(i,j)$转移概率是任意的，可以选其为合适的容易抽样的概率分布，按照上面拒绝采样的方法就相当于，首先在$q(i,:)$抽样出状态$j$，然后有$\alpha(i,j)$的概率接受该样本，应该如何证明在$j\sim Q(x\mid i)$中抽样等价于在$j\sim q(i,x)$，然后再以$\alpha(i,j)$概率接受该抽样，并且$Q_{i,j} = q(i,j)\alpha(i,j)$，设抽样为$z\sim q(z)$，接受率为$\alpha(z)$，则

$$p(z, Acc=True) = q(z)\alpha(z) \\ p(Acc=True) = \sum_z q(z)\alpha(z)$$

这时如果$q(z)\alpha(z)$确实是一个关于$z$的概率分布的话，那么$p(Acc=True) = \sum_z q(z)\alpha(z) = 1$，这个地方有点问题。。。

---

以下面代码中例子为例，$q = uniform(-2.5, 5)$，则

$$\begin{split} p(i,j,Acc=True) & = p(i)q(i,j)\alpha(i,j) \\ p(Acc=True) & = \sum_{i,j}p(i,j,Acc=True) \\ & = \sum_{i,j}p(i)q(i,j)\alpha(i,j) \\ & = \sum_{i,j}p(i)q(i,j)p(j)q(j,i) \\ & = \sum_{i,j}p(i)\frac{1}{7.5}p(j)\frac{1}{7.5} \\ & = \frac{1}{7.5^2} \sum_ip(i)\sum_jp(j) \\ & = \frac{1}{7.5^2} \end{split}$$

故实际迭代次数大致为所求样本个数的$7.5^2=56.26$倍
同样

$$\begin{split} p(Acc=True, i) & = \sum_{j}p(i,j,Acc=True) \\ & = \sum_{j}p(i)q(i,j)\alpha(i,j) \\ & = \sum_{j}p(i)q(i,j)p(j)q(j,i) \\ & = \sum_{j}p(i)\frac{1}{7.5}p(j)\frac{1}{7.5} \\ & = \frac{1}{7.5^2} \sum_jp(j)p(i) \\ & = \frac{1}{7.5^2}p(i) \\ p(j\mid i, Acc=True) & = \frac{p(j, i, Acc=True)}{p(i, Acc=True)} \\ & = p(j) \end{split}$$

def q(y, x): # q(y|x)
    return 1/(5. - (-2.5))
def sample_q(x):
    return np.random.uniform(low=-2.5, high=5.)

def mcmc(p, q, sample_q, size, base_iter=10**2):
    res = []
    it = 0
    x = 0.
    ti = 0
    while it < size + base_iter:
        y = sample_q(x)
        u = np.random.uniform(low=0, high=1)
        if u <= p(y)*q(x, y):
            x = y
            it += 1
        res.append(x)
        ti += 1
    return np.array(res)[base_iter:], ti

x = np.linspace(-2, 4, 10000) 
y = p(x)

sample, ti = mcmc(p, q, sample_q, 10**4)
count, bins, ignored = plt.hist(sample, bins=300,density=True)
plt.plot(bins, p(bins))

[<matplotlib.lines.Line2D at 0x15bbf406940>]

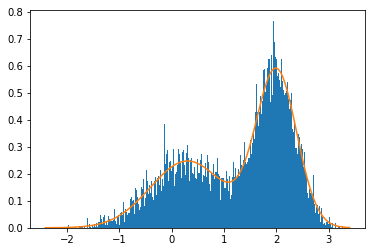
ti

561925

Metropolis Hastings

由细致平稳条件

$$p(i)q(i,j)\alpha(i,j) = p(j)q(j,i)\alpha(j,i)$$ 两边同乘以一个系数不改变平稳条件，但却使得每次抽样的接受率变大，故Metropolis Hastings算法的思想是，在方程两边同乘以一个系数使得两边的接受率的较大值扩展到1，于是
$$\alpha(i,j) = \min\left\{ \frac{p(j)q(j,i)}{p(i)q(i,j)}, 1 \right\}$$

def Metropolis_Hastings(p, q, sample_q, size, base_iter=10**2):
    res = []
    it = 0
    x = 0.
    ti = 0
    while it < size + base_iter:
        y = sample_q(x)
        u = np.random.uniform(low=0., high=1)
        a = min(p(y) / p(x) * q(y, x) / q(x, y), 1)
        if u < a:
            x = y
            it += 1
        res.append(x)
        ti += 1
    return np.array(res)[base_iter:], ti

sample, ti = Metropolis_Hastings(p, q, sample_q, 10**4)
count, bins, ignored = plt.hist(sample, bins=300,density=True)
plt.plot(bins, p(bins))

[<matplotlib.lines.Line2D at 0x15bbf76eb70>]

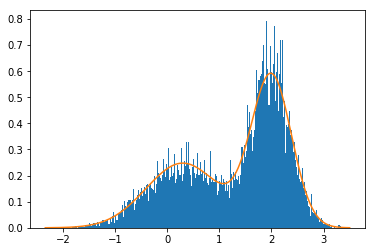
ti

27495

---

这个地方需要注意，原始写的有点问题，每次抽样出来的样本都需要加入到总体样本中，这样的话，其跟拒绝采样的不同点在于MCMC不抛弃样本，只根据当前状态判断是否跳转