@zsh-o
2018-03-22T12:47:33.000000Z
字数 4363
阅读 1604
无模型 最近邻 概率密度估计
机器学习
源自学长的一篇论文
考虑一个分类问题:,样本集:
对一个新样本,我们要计算其类别,考虑贝叶斯规则:
由此只需要计算出和即可
先计算,考虑的分布,单纯的产生是相互独立的并服从多项式分布,,设,也即只有发生事件的那个为,这样分布就可以用乘法表示
并且
在数据集的似然函数为
设,代表了发生的次数,也就是上面的发生的次数
对数似然
对其求极大值,并且要满足上面的约束条件,所以用拉格朗日乘数法
解方程得
也即是,多项式分布的参数是在整个数据集中各个统计值所占的比例
接下来计算,由于为连续的,所以其表示在整个输入空间中的条件密度函数,我们的主要目的就是根据现有的观测值,估计出该密度函数,也就是说要估计出联合概率分布函数,任何一个密度估计函数都可以用到这个地方。因为每个X有多个属性,所以在估计的时候要考虑属性之间的相关关系。现在的问题变成了如何估计样本全部属性的联合概率函数
首先,我们无法直接估计该函数,因为,如果直接根据样本得到该函数每一个点的位置,这个在连续属性中肯定是不可能的(连续属性有无穷多个位置),即使到离散里面,这样简单的估计也是很不准确的,因为这种直接估计的方法的自由度太大,需要得到的值太多,相应的,就需要非常多而且能覆盖几乎所有空间的样本,这样基本上是不现实的。另外一种降低自由度的方法就是参数估计,假设每一个单个属性或者多个属性组符合一个参数化的分布(通常是指数族分布),再根据属性之间的相关性来估计最佳的参数,这种做法的缺点是太依赖先验,每个属性的参数化分布的形式、属性之间的相关关系等。
学长这个地方用了一种“新奇”的估计方法,利用近邻法则,直接根据新样本和已有的观测数据,直接获得该样本在个值中的联合概率,然后利用上面的贝叶斯公式计算出所有的,则的类别就是概率最大的类别。这个方法依据样本与其他所有同类别样本的最短距离来计算,他这里用的是欧式距离
首先定义了一个,代表最短距离大于等于的概率,
学长这里对进行求导,我这里不是太明白这个式子是怎么来的,学长是这样说的
我们知道随着的增加将会减少,的减少量正比于样本两侧的其他间隔的个样本点,关系公式如下所示
接下来就是解这个微分方程,设,得,,再有上面的
首先来看一下,与最近邻距离的概率之间的关系
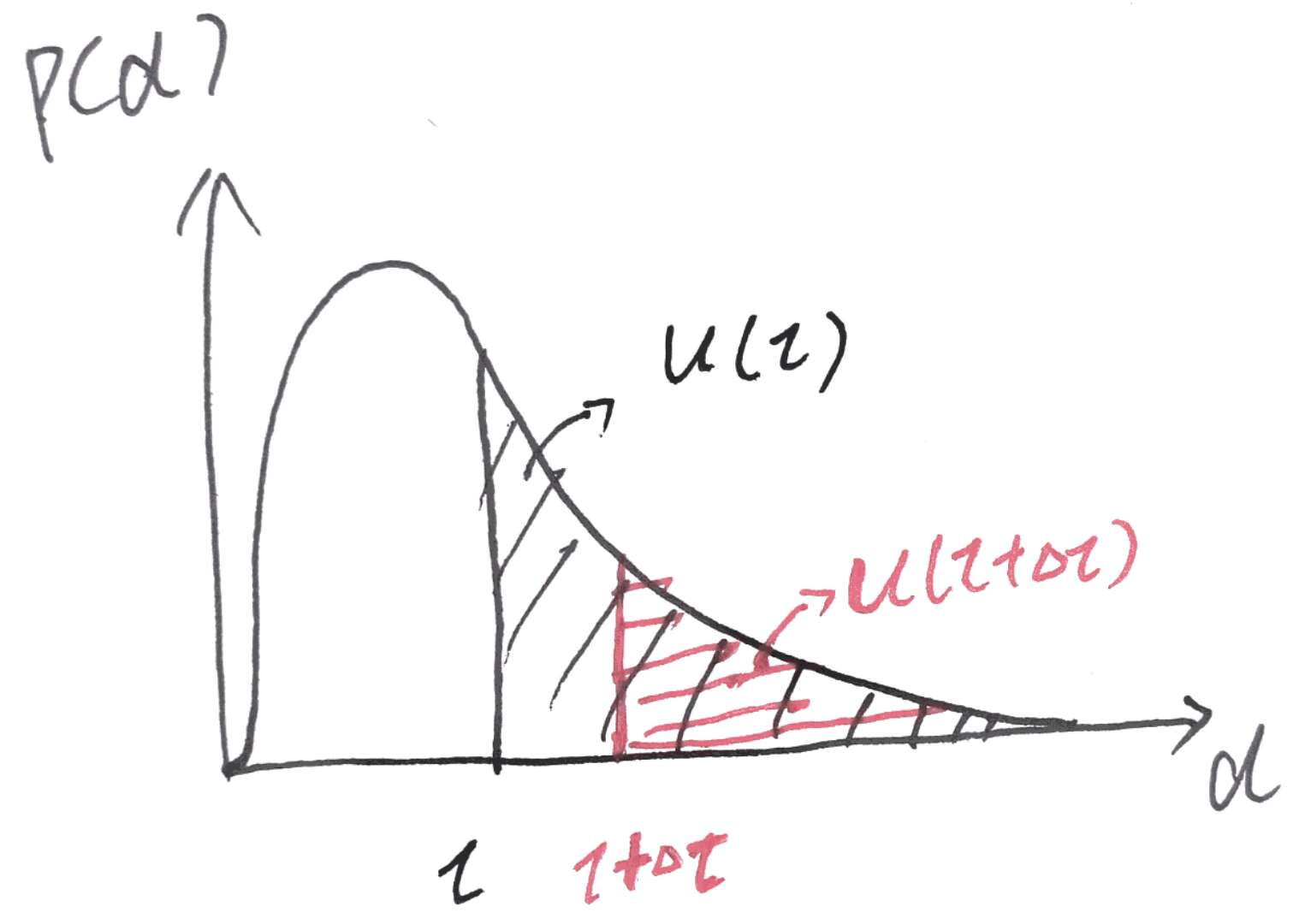
由此
然后学长通过计算的期望来计算的概率,为的最近邻距离
然后在这里,又一处我不是很理解的地方,学长直接让函数的期望等于函数本身
这个等式怎么来的不知道,这里应该有什么高深的数学知识我不知道。根据这个等式很容易求出联合分布
这里算出来的概率是同一类别下的,最近点也是同一类别下的最近点,最终要再除以归一项,在各个类别下计算出的值的和
接下来是扩展到多维的,思路类似,由于有两个地方没弄明白,不急着往后
先整理下现在有的东西
- :最短距离至少为的概率
- :最短距离等于的概率
- :半径为的维球的体积,
- :条件联合概率密度函数
- :函数的期望,这里为样本的最近距离
不明白的两个公式
关于第二条不明白的地方:本身就表示在训练集里面距离样本最近距离,该距离就是一个唯一的值?(啊哈~),那么这个地方的就表示这个函数的预期的结果,是计算出来的,而后面的是实际的结果,因为前面一整套均是一个估计值,而最近距离才是观测值,那么用此处的等式相等来得出想要的联合概率密度函数也就能说的过去
