LDA变分EM 与 指数分布族

机器学习

---

看LDA的变分EM解法中有提到用指数分布族归一化项的一阶导数就是期望值，这里整理一下

指数分布族

指数分布族符合如下形式：

$$p(x\mid \theta) = h(x)\exp\big(\eta(\theta)*T(x) - A(\theta)\big)$$

• $\theta$：自然参数
• $h(x)$：底层观测值
• $T(x)$：充分统计量
• $A(\theta)$：对数规则化，归一化因子

多维情况下（参数和随机变量均为向量）可表示为

$$\begin{split} p(\mathbf{x}\mid \boldsymbol{\theta}) & = h(\mathbf{x})\exp\big(\boldsymbol{\eta(\theta)}\cdot \mathbf{T(x)} - \mathbf{A(\boldsymbol\theta)}\big) \\ & = h(\mathbf{x})\exp\left(\sum_{i=1}^s \eta_i(\boldsymbol{\theta})T_i(\mathbf{x}) - \mathbf{A(\boldsymbol\theta)}\right) \end{split}$$

狄利克雷分布$\vec{p} \sim Dir(\mathbf{\vec{\alpha}})$：

$$\begin{split} P(\vec{p}\mid \vec{\alpha}) & = \frac{\Gamma(\sum_i \alpha_i)}{\prod_i\Gamma(\alpha_i)}\prod_i p_i^{\alpha_i -1} \\ & = \exp\left( \log \prod_i p_i^{\alpha_i-1} - \log\frac{\prod_i \Gamma(\alpha_i)}{\Gamma(\sum_i \alpha_i)} \right) \\ & = \exp\left( \sum_i (\alpha_i-1)\log p_i - \bigg( \Big\{ \sum_i \log \Gamma(\alpha_i)\Big\}-\log\Gamma\big(\sum_i \alpha_i\big) \bigg) \right) \end{split}$$
对应上面的形式

• $h(x) = 1$
• $T_i(x) = \log x_i$
• $\eta_i(\theta) = \alpha_i-1$
• $A(\theta) = \Big\{ \sum_i \log \Gamma(\alpha_i)\Big\}-\log\Gamma\big(\sum_i \alpha_i\big)$

指数分布族 性质

对指数族分布对$x$积分

$$\begin{split} \int_x p(x\mid \theta) \mathrm{d}x = \int_x h(x)\exp\Big( \eta(\theta)\cdot T(x) - A(\theta) \Big) = 1 \end{split}$$
对上式取 $\eta(\theta)$的导数
$$\begin{split} \frac{\mathrm{d}}{\mathrm{d}\eta(\theta)} \int_x p(x\mid \theta) \mathrm{d}x & = \int_x\frac{\mathrm{d}}{\mathrm{d}\eta(\theta)} p(x\mid \theta) \mathrm{d}x \\ & = \int_x h(x)\exp\Big( \eta(\theta)\cdot T(x) - A(\theta) \Big) \cdot \Big( T(x) - \frac{\mathrm{d}}{\mathrm{d}\eta(\theta)}A(\theta)\Big) \mathrm{d}x \\ & = \int_x p(x\mid \theta)\cdot \Big( T(x) - \frac{\mathrm{d}}{\mathrm{d}\eta(\theta)}A(\theta) \Big)\mathrm{d}x \\ & = 0 \end{split}$$
得，
$$\begin{split} & \int_x p(x\mid \theta)\cdot \Big( T(x) - \frac{\mathrm{d}}{\mathrm{d}\eta(\theta)}A(\theta) \Big)\mathrm{d}x = 0 \\ & \int_x p(x\mid \theta)\cdot T(x) \mathrm{d}x = \int_x \frac{\mathrm{d}}{\mathrm{d}\eta(\theta)}A(\theta)\mathrm{d}x = \frac{\mathrm{d}}{\mathrm{d}\eta(\theta)} A(\theta) \\ & E_p[T(x)] = \frac{\mathrm{d}}{\mathrm{d}\eta(\theta)}A(\theta) \end{split}$$

多维情况下形式相同

$$E_p[T_i(x)] = \frac{\mathrm{d}}{\mathrm{d}\eta_i(\theta)}A(\theta)$$

应用于上面的狄利克雷分布

$$\begin{split} E_p[T_i(x)] & = E_p[\log p_i] \\ & = \frac{\mathrm{d}}{\mathrm{d}\eta_i(\theta)}A(\theta) \\ & = \frac{\mathrm{d}}{\mathrm{d}(\alpha_i-1)} \bigg( \Big\{ \sum_i \log \Gamma(\alpha_i)\Big\}-\log\Gamma\big(\sum_j \alpha_j\big) \bigg) \\ & = \frac{\Gamma'(\alpha_i)}{\Gamma(\alpha_i)} - \frac{\Gamma'\big( \sum_j \alpha_j \big)}{\Gamma\big(\sum_j\alpha_j\big)} \\ & = \Psi(\alpha_i) - \Psi(\small\sum_j\normalsize\alpha_j ) \end{split}$$

LDA - 变分EM

回到LDA模型，里面有三个中间隐含变量$(\theta\in\mathcal{R}^{D}, z\in \mathcal{R}^{D\times N}, \beta\in \mathcal{R}^K)$，分别用三个辅助变量来估计$\gamma\rightarrow\theta, \phi\rightarrow z,\lambda\rightarrow\beta$

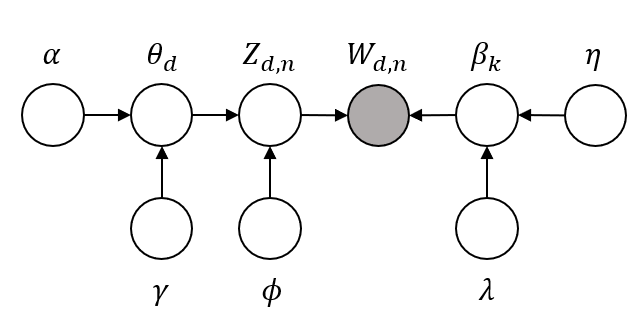
EM的E-step用以确定出$q$分布的形式，这里也就是求出$q(\theta), q(z), q(\beta)$

首先来看看单纯的EM
从两个方向均可推出EM的公式，从对数似然出发和从KL散度出发
从对数似然出发，

$$\begin{split} \mathcal{L}(\mathcal{W}\mid \alpha,\eta) & = \log\prod_w p(w\mid \alpha, \eta)\\ & = \sum_w \log p(w\mid \alpha, \eta)\\ & = \sum_w \log \iiint p(\theta,\beta,z,w \mid \alpha, \eta)\mathrm{d}\theta \mathrm{d}\beta\mathrm{d}z \\ & = \sum_w \log \iiint Q_w(\theta, \beta, z) \frac{p(\theta, \beta, z, w \mid \alpha, \eta)}{Q_w(\theta, \beta, z)}\mathrm{d}\theta\mathrm{d}\beta\mathrm{d}z \\ & = \sum_w \log E_{Q_w}\Big[ \frac{p(\theta, \beta, z, w\mid \alpha, \eta)}{Q_w(\theta, \beta, z)} \Big] \\ & \geq \sum_w E_{Q_w}\Big[ \log \frac{p(\theta, \beta, z, w\mid \alpha, \eta)}{Q_w(\theta, \beta, z)} \Big] \\ \end{split}$$
在EM中需要找到函数$Q_w(\theta, \beta, z)$的形式，使$\mathcal{L}(w\mid \alpha, \eta)$最小，也就是要使上式变为等号，而且当$f$为凸函数时，$E_p[f(x)]\geq f(E_p[x])$，当且仅当$f=\mathcal{C}$为常数时为等号，故
$$\begin{split} \frac{p(\theta, \beta, z, w\mid \alpha, \eta)}{Q_w(\theta, \beta, z)} & = \mathcal{C} \\ p(\theta, \beta, z, w\mid \alpha, \eta) & = \mathcal{C}\cdot Q_w(\theta, \beta, z)\\ \iiint p(\theta, \beta, z, w\mid \alpha, \eta)\mathrm{d}\theta\mathrm{d}\beta\mathrm{d}z & = \mathcal{C}\iiint\cdot Q_w(\theta, \beta, z)\mathrm{d}\theta\mathrm{d}beta\mathrm{d}z \\ p(w\mid \alpha, \eta) & = \mathcal{C} \end{split}$$
由此得出在现有观测值$w$下的$Q$的形式
$$Q_w(\theta, \beta, z) = \frac{p(\theta, \beta, z, w\mid \alpha, \eta)}{p(w\mid \alpha, \eta)}$$

---

遇到了一个问题：为什么EM不能直接求出来而是用变分EM，在E-step的时候用变分的方法求出三个分布的最优估计值，其实求出来的是具体的值

---

Reference

• 文本主题模型之LDA(三) LDA求解之变分推断EM算法