@zsh-o
2018-04-11T00:59:05.000000Z
字数 10700
阅读 5537
最速降线 与 第一次接触泛函
数学
现在看得很多内容都提到了变分和泛函,本科只学了高数,现在也看一下变分的内容
斯涅尔定律
当光穿过不同介质时,由于在不同介质之间的传播速率不同,会发生折射现象,其入射光和折射光在同一平面,而且与法线夹角满足:
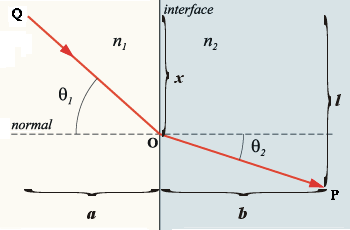
证明折射定律可以使用费马原理
费马原理:
“最短时间原理”:光线传播的路径是需时最少的路径
“平稳时间原理”:光沿着所需时间为平稳的路径传播
光从点传播到点所需要的时间为
根据费马原理,光线传播路径是所需时间为极值的路径,则
最速降线
由上面的折射定律可知,在速度v已知的情况下,要满足所用时间最少,需要保证
根据能量守恒定律
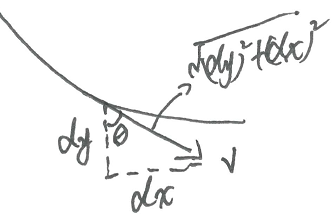
在每一点速度方向与法线夹角,它与该点的微元满足
组合公式得
整理得,
泛函与变分法
函数是数域到数域的映射,,而表示两个数之间的差值,而泛函是定义域是函数值域是实数的映射,是从函数组成的一个向量空间到实数的一个映射,表示两个函数之间的差值,也是一个函数。
设是一个由函数组成的集合,对于中的任意一个元素,数集都有一个元素与之对应,称是的泛函数
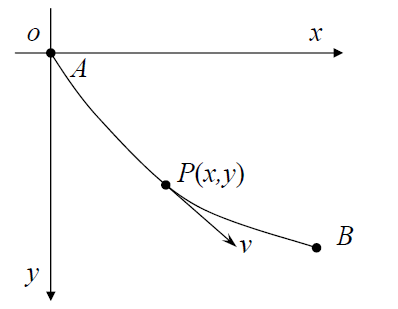
假设我寻找连接两点的一条曲线并且这条曲线能够使泛函取得极值
泛函经常用积分来表示,而我们则要求该积分的极值
而求解该极值的方法就是变分法。为的变分,当变为时,对应的泛函变为,当趋于无穷小时,可以用一个一阶线性来逼近处的曲线
那么泛函的变分为
接下来证明泛函取极值的必要条件是
我们有一函数满足
那么在两端点值函数的改变量为0,所以
这样泛函
我们考虑,这时如果能够使泛函满足极值,也就是说,这时,对求偏导,并且当时偏导为
然后用乘以上式,并依据
接下来需要证明
- A:
- B:
- C:
- D: C->D:
- D: B->D:
两式相等得,
再根据分布积分
带入原式得到泛函的变分
由于可取任意函数形式(也可以用反证法来证),就可以得到欧拉-拉格朗日方程(E-L方程)
接下来证一个引理
若,则欧拉方程可改写成
故,
变分法表达最速降线
现在回到最速降线问题,并用变分法解决
已知
因此可以得到时间的泛函
由于最速下降曲线问题满足上面的引理,直接用该引理(也可以直接求,过程类似)
整理可得
求解最速降线
上面只是用两种方法得到最速降线的表达形式,现在来解出该方程,也就是求解该微分方程
上式的形式是一个三角函数,设是关于的函数,,由于是关于的微分,故不能由直接求出关于的方程,把带入上式得
再有
由此得到方程
由于,所以这个就是切线与法线夹角,所以端点值,得到,并把,就可以得到最速降线的参数方程
由此可知,最速降线是一条摆线,是由一个圆沿一条直线运动时,圆边界上一定点所形成的轨迹
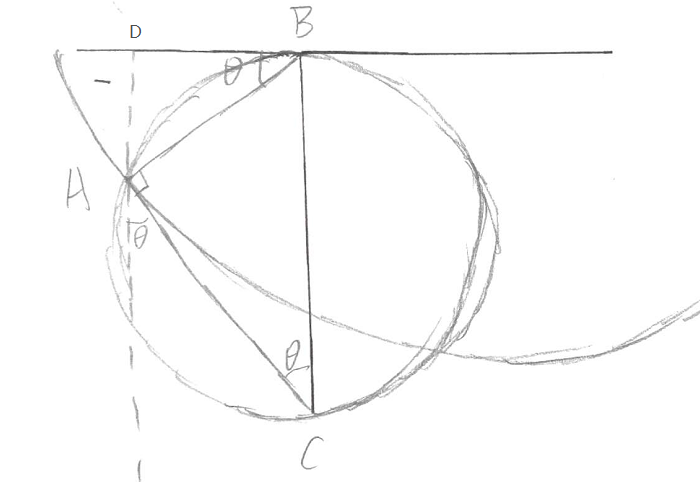
点为该定点,为速度方向也是该摆线在点的切线,由此,为上面的速度与法线的夹角,可以得到,设该圆半径为,则
AD为A点的纵坐标,比较上面两式得到生成摆线圆的半径
最后证明两条最速降线的性质
性质一:生成最速降线轨迹的圆是匀速的
要证明这条性质,我们只需要找到点的横坐标与之间的关系即可
对摆线式子进行求导得
故圆按速度匀速前进
性质二:等时性
最速降线的等时性是说,无论从最速降线的哪一点无速度的开始,到达最底端所用的时间相同
假设小球(啊哈)从高度下降到,根据能量守恒得,
故所用时间与或无关
再说一点
用上面的方法求解出来的最速下降曲线是一种摆线,而只给出了摆线的参数方程,而该参数方程可以表示很多很多条摆线,我们要做的就是把端点值带入求解摆线的参数,但这个参数好像求不出来
