[关闭]
@zsh-o 2018-07-09T08:51:38.000000Z 字数 6670 阅读 1152

5 - 决策树

《统计学习方法》

  1. %matplotlib inline
  2. import numpy as np
  3. from matplotlib import pyplot as plt
  4. epsilon = 1e-5
  5. np.seterr(divide='ignore',invalid='ignore')
{'divide': 'warn', 'over': 'warn', 'under': 'ignore', 'invalid': 'warn'}

  1. import pydot
  2. from IPython.display import Image, display
  4. def viewPydot(pdot):
  5.     plt = Image(pdot.create_png())
  6.     display(plt)
  1. ## 给定离散的概率，求熵，e为底
  2. def H(P):
  3.     P = P + epsilon
  4.     return -(np.sum(P * np.log2(P)))
  1. def information_gain(X, Y):
  2.     N, M = X.shape
  3.     K = np.max(Y) + 1
  4.     SX = np.max(X, axis=0) + 1
  5.     NY = np.zeros(K)
  6.     for i in range(K):
  7.         NY[i] = np.count_nonzero(Y==i)
  8.     NX = []
  9.     for m in range(M):
  10.         NX_i = np.zeros((SX[m],1))
  11.         for i in range(SX[m]):
  12.             NX_i[i,0] = np.count_nonzero(X[:, m]==i)
  13.         NX.append(NX_i)
  14.     HX = H(NY / N)
  15.     NY_A = []
  16.     for i in range(M):
  17.         NY_Ai = np.zeros((SX[i], K))
  18.         for j in range(SX[i]):
  19.             t = Y[X[:, i]==j]
  20.             for k in range(K):
  21.                 NY_Ai[j, k] = np.count_nonzero(t==k)
  22.         NY_A.append(NY_Ai)
  24.     PY_A = []
  25.     PX = []
  26.     for m in range(M):
  27.         PY_A.append(NY_A[m] / NX[m]) ## NY_A[m][i, k] / NX[m][i] ## p(Y = y_k | X^m = i)
  28.         PX.append(NX[m] / N)
  29.     HY_X = []
  30.     for m in range(M):
  31.         HY_Xi = np.zeros(SX[m])
  32.         for i in range(SX[m]):
  33.             HY_Xi[i] = H(PY_A[m][i, :])
  34.         HY_X.append(HY_Xi)
  35.     HY_A = np.zeros(M)
  36.     for m in range(M):
  37.         HY_A[m] = np.sum(HY_X[m] * PX[m].reshape(-1)) ## numpy由于有Broadcasting存在，所以写程序的时候一定要注意维度要匹配 https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html
  38.     HA_X = np.zeros(M)
  39.     for m in range(M):
  40.         HA_X[m] = H(NX[m] / N)
  41.     gain = HX - HY_A
  42.     return gain, gain / HA_X
  1. X = np.array([
  2.     [0, 0, 0, 0, 0],
  3.     [0, 0, 0, 1, 0],
  4.     [0, 1, 0, 1, 1],
  5.     [0, 1, 1, 0, 1],
  6.     [0, 0, 0, 0, 0],
  7.     [1, 0, 0, 0, 0],
  8.     [1, 0, 0, 1, 0],
  9.     [1, 1, 1, 1, 1],
  10.     [1, 0, 1, 2, 1],
  11.     [1, 0, 1, 2, 1],
  12.     [2, 0, 1, 2, 1],
  13.     [2, 0, 1, 1, 1],
  14.     [2, 1, 0, 1, 1],
  15.     [2, 1, 0, 2, 1],
  16.     [2, 0, 0, 1, 0],
  17. ])
  18. Y = X[:, -1]
  19. Y = Y.reshape((-1,1))
  20. X = X[:, :-1]
  1. information_gain(X, Y)
(array([0.08300555, 0.32359689, 0.41990845, 0.29479317]),
 array([0.05237053, 0.35239124, 0.43247518, 0.1926588 ]))

  1. class TreeNode(object):
  2.     def __init__(self, prop=None, Nprop=None, label=None):
  3.         self.children = dict()
  4.         self.prop = prop
  5.         self.Nprop = Nprop
  6.         self.label = label
  7.         self.leaf = False
  1. def ID3(X, Y, threshold):
  2.     N, M = X.shape
  3.     K = np.max(Y) + 1
  4.     SX = np.max(X, axis=0) + 1
  5.     def build_tree(cX, cY):
  6.         NcY = np.zeros(K)
  7.         unique_Y = np.unique(cY)
  8.         if len(unique_Y)==1:  ## 属于同一类
  9.             t = TreeNode()
  10.             t.label = unique_Y[0]
  11.             t.leaf = True
  12.             return t
  13.         for i in range(K):
  14.             NcY[i] = np.count_nonzero(cY==i)
  15.         gain, ratio = information_gain(cX, cY)
  16.         iP = np.argmax(gain)
  17.         max_gain = gain[iP]
  18.         t = TreeNode(prop=iP, Nprop=SX[iP], label = np.argmax(NcY))
  19.         if max_gain < threshold:
  20.             t.leaf = True
  21.             return t
  22.         for i in range(SX[iP]):
  23.             cindex = (cX[:,iP] == i)
  24.             t.children[i] = build_tree(cX[cindex], cY[cindex])
  25.         return t
  26.     return build_tree(X, Y)
  1. root = ID3(X, Y, 0.)
  1. dot = pydot.Dot()
  2. global level
  3. level = 1
  4. def create_dot(p):
  5.     global level
  6.     p_name = "%d # %s, %s, %s" % (level, str(p.prop), str(p.Nprop), str(p.label))
  7.     dot.add_node(pydot.Node(name=p_name))
  8.     if p.prop == None:
  9.         return
  10.     for i in range(p.Nprop):
  11.         level = level + 1
  12.         c = p.children[i]
  13.         c_name = "%d # %s, %s, %s" % (level, str(c.prop), str(c.Nprop), str(c.label))
  14.         dot.add_edge(pydot.Edge(dst=c_name, src=p_name))
  15.         create_dot(c)
  16.         level = level -1
  1. create_dot(root)
  2. viewPydot(dot)

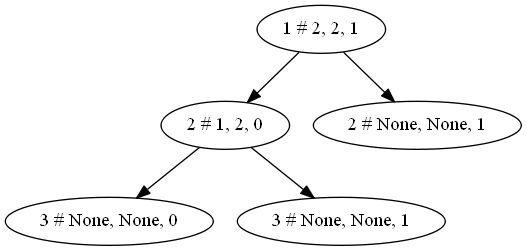
output_11_0.png-21kB

剪枝

前序遍历计算每个节点的H，后续遍历对有叶节点进行剪枝

  1. class TreeNode(object):
  2.     def __init__(self, prop=None, Nprop=None, label=None):
  3.         self.children = dict()
  4.         self.prop = prop
  5.         self.Nprop = Nprop
  6.         self.label = label
  7.         self.leaf = False
  8.         self.H = None
  10. def ID3(X, Y, threshold):
  11.     N, M = X.shape
  12.     K = np.max(Y) + 1
  13.     SX = np.max(X, axis=0) + 1
  14.     global visited
  15.     visited = np.zeros(M, dtype=np.bool)
  16.     def build_tree(cX, cY):
  17.         global visited
  18.         NcY = np.zeros(K)
  19.         unique_Y = np.unique(cY)
  20.         if len(unique_Y)==1:  ## 属于同一类
  21.             t = TreeNode()
  22.             t.label = unique_Y[0]
  23.             t.leaf = True
  24.             t.H = 0.
  25.             return t
  26.         for i in range(K):
  27.             NcY[i] = np.count_nonzero(cY==i)
  28.         gain, ratio = information_gain(cX, cY)
  29.         gain[visited] = - np.inf
  30.         iP = np.argmax(gain)
  31.         if len(np.unique(cX[:,iP]))==1:
  32.             t1 = TreeNode(prop=None, Nprop=None, label=np.argmax(NcY))
  33.             t1.H = H(NcY / len(cY))
  34.             t1.leaf = True
  35.             return t1
  36.         max_gain = gain[iP]
  37.         t = TreeNode(prop=iP, Nprop=SX[iP], label = np.argmax(NcY))
  38.         t.H = H(NcY / len(cY))
  39.         if max_gain < threshold:
  40.             t.leaf = True
  41.             return t
  42.         visited[iP] = True
  43.         for i in range(SX[iP]):
  44.             cindex = (cX[:,iP] == i)
  45.             t.children[i] = build_tree(cX[cindex], cY[cindex])
  46.         visited[iP] = False
  47.         return t
  48.     return build_tree(X, Y)
  1. root = ID3(X, Y, 0.)
  1. dot = pydot.Dot()
  2. global level
  3. level = 1
  4. def create_dot(p):
  5.     global level
  6.     p_name = "%d # %s, %s, %s, %.3f" % (level, str(p.prop), str(p.Nprop), str(p.label), p.H)
  7.     dot.add_node(pydot.Node(name=p_name))
  8.     if p.leaf is True:
  9.         return
  10.     for i in range(p.Nprop):
  11.         level = level + 1
  12.         c = p.children[i]
  13.         c_name = "%d # %s, %s, %s, %.3f" % (level, str(c.prop), str(c.Nprop), str(c.label), c.H)
  14.         dot.add_edge(pydot.Edge(dst=c_name, src=p_name))
  15.         create_dot(c)
  16.         level = level -1
  18. create_dot(root)
  19. viewPydot(dot)

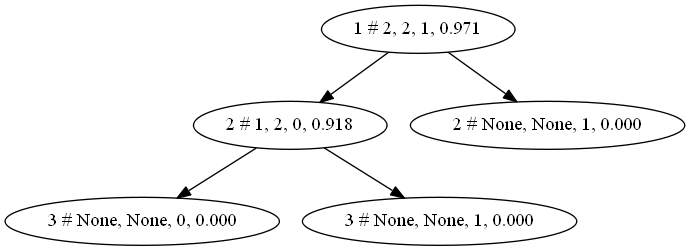
output_15_0.png-26.6kB

  1. Watermelon = np.array([
  2.     [0, 0, 0, 0, 0, 0, 0],
  3.     [1, 0, 1, 0, 0, 0, 0],
  4.     [1, 0, 0, 0, 0, 0, 0],
  5.     [0, 0, 1, 0, 0, 0, 0],
  6.     [2, 0, 0, 0, 0, 0, 0],
  7.     [0, 1, 0, 0, 1, 1, 0],
  8.     [1, 1, 0, 1, 1, 1, 0],
  9.     [1, 1, 0, 0, 1, 0, 0],
  10.     [1, 1, 1, 1, 1, 0, 1],
  11.     [0, 2, 2, 0, 2, 1, 1],
  12.     [2, 2, 2, 2, 2, 0, 1],
  13.     [2, 0, 0, 2, 2, 1, 1],
  14.     [0, 1, 0, 1, 0, 0, 1],
  15.     [2, 1, 1, 1, 0, 0, 1],
  16.     [1, 1, 0, 0, 1, 1, 1],
  17.     [2, 0, 0, 2, 2, 0, 1],
  18.     [0, 0, 1, 1, 1, 0, 1],
  19. ])
  20. Y = Watermelon[:, -1]
  21. Y = Y.reshape((-1,1))
  22. X = Watermelon[:, :-1]
  1. root = ID3(X, Y, 0.)
  1. dot = pydot.Dot()
  2. create_dot(root)
  3. viewPydot(dot)

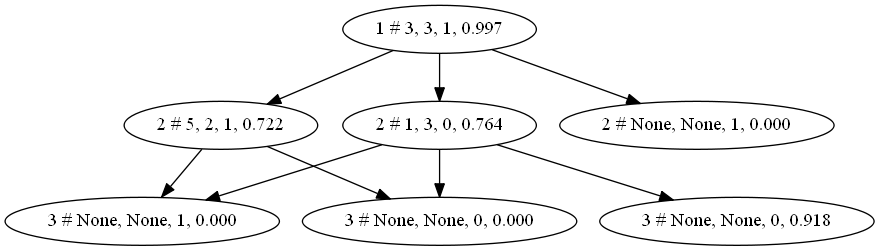
output_18_0.png-38.5kB

不是leaf并且子节点的leaf==true

  1. def pruning(root, threshold):
  2.     if root.leaf is True:
  3.         return;
  4.     print(root.H, root.leaf)
  5.     for p in root.children.values():
  6.         pruning(p, threshold)
  7.     if root.children[0].leaf is True:
  8.         t = 0.
  9.         l = len(root.children)
  10.         for p in root.children.values():
  11.             t = t + p.H
  12.         if t - root.H < (l-1) * threshold:
  13.             for i in range(l):
  14.                 root.children[i] = None
  15.                 root.leaf = True
  1. pruning(root, .0)
0.9974937421855691 False
0.764200977141265 False
0.7219256790976065 False

  1. dot = pydot.Dot()
  2. create_dot(root)
  3. viewPydot(dot)

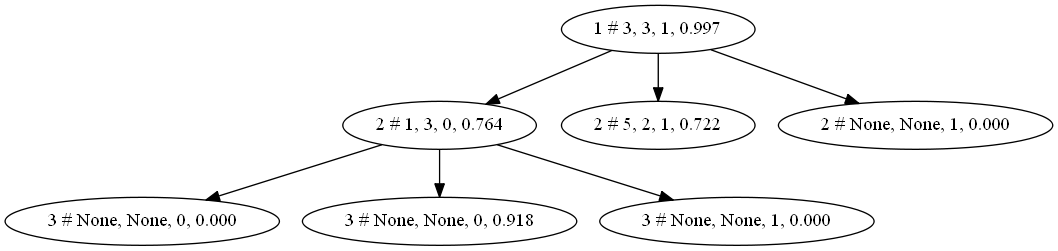
output_22_0.png-37kB

CART

需要在当前节点对应的数据集下计算所有属性和属性值对应的Gini指数，对最大Gini指数的进行划分，小于阈值跳出

  1. class TreeNode(object):
  2.     def __init__(self, prop, value, label):
  3.         self.prop = prop
  4.         self.value = value
  5.         self.label = label
  6.         self.lc = None
  7.         self.rc = None
  8.         self.leaf = False
  9.         self.N_leaf = 0
  10.         self.H = 0.
  11.         self.g = 0.
  1. def CART_C(X, Y, threshold, purning_thre):
  2.     N, M = X.shape
  3.     SX = np.max(X, axis=0) + 1
  4.     K = np.max(Y) + 1
  5.     global visited
  6.     visited = []
  7.     for m in range(M):
  8.         visited.append(np.zeros(SX[m], dtype=np.bool))
  9.     def build_tree(cX, cY):
  10.         global visited
  11.         PX_Y = []
  12.         for m in range(M):
  13.             PXi = np.zeros((SX[m], K))
  14.             for i in range(SX[m]):
  15.                 index = (cX[:, m] == i)
  16.                 iY = cY[index]
  17.                 l = len(iY)
  18.                 for k in range(K):
  19.                     PXi[i, k] = len(np.where(iY==k)[0]) / (l+epsilon)
  20.                     if l == 0:
  21.                         PXi[i, k] = 1
  22.             PX_Y.append(PXi)
  23.         ginis = []
  24.         mginis = np.zeros(M)
  25.         mindex = np.zeros(M, dtype=np.int)
  26.         for m in range(M):
  27.             PXi = PX_Y[m]
  28.             gs = 1 - np.sum(np.power(PXi, 2), axis=1)
  29.             gs[visited[m]] = -np.inf
  30.             mm = np.argmax(gs)
  31.             mindex[m] = mm
  32.             mginis[m] = gs[mm]
  33.         mpi = np.argmax(mginis)
  34.         mpii = mindex[mpi]
  35.         mmg = mginis[mpi]
  36.         t = TreeNode(prop=mpi, value=mpii, label=np.argmax(PX_Y[mpi][mpii,:]))
  37.         t.H = H(PX_Y[mpi][mpii,:])
  38.         if mmg <= (threshold+epsilon):
  39.             t.leaf = True
  40.             t.N_leaf = 1
  41.             t.g = 0.
  42.             return t
  43.         t.leaf = False
  44.         visited[mpi][mpii] = True
  45.         index = (cX[:, mpi] == mpii)
  46.         t.lc = build_tree(cX[index], cY[index])
  47.         t.rc = build_tree(cX[np.logical_not(index)], cY[np.logical_not(index)])
  48.         t.N_leaf = t.lc.N_leaf + t.rc.N_leaf
  49.         visited[mpi][mpii] = False
  50.         return t
  51.     root = build_tree(X, Y)
  52.     return root
  1. root = CART_C(X, Y, 0.45, 0.1)
  1. dot = pydot.Dot()
  2. global level
  3. level = 1
  4. def create_dot(p):
  5.     global level
  6.     p_name = "%s # %s, %s, %s, %.3f" % (p.__str__(), str(p.prop), str(p.value), str(p.label), p.H)
  7.     dot.add_node(pydot.Node(name=p_name))
  8.     if p.leaf is True:
  9.         return
  10.     for c in [p.lc, p.rc]:
  11.         level = level + 1
  12.         c_name = "%s # %s, %s, %s, %.3f" % (c.__str__(), str(c.prop), str(c.value), str(c.label), c.H)
  13.         dot.add_edge(pydot.Edge(dst=c_name, src=p_name))
  14.         create_dot(c)
  15.         level = level -1
  17. create_dot(root)
  18. viewPydot(dot)

output_28_0.png-301kB

添加新批注
在作者公开此批注前，只有你和作者可见。
回复批注