旅行商问题 与 状态压缩

算法

---

问题描述

上周末遇到的某笔试题，就是经典的旅行商问题，以前没写过，现在写下来记录一下

问题大意是，毕业了要进行毕业旅行，打算从北京出发，途径几个城市，最后回到北京。要求每个沿途城市只去一次，并且最终花费最小。

输入：

• 城市个数$n$（$1 < n \le 20$，包括北京）
• 每个城市间的路费，$n$行$n$列的矩阵$S[n][n]$

4
0 2 6 5
2 0 4 4
6 4 0 2
5 4 2 0

输出：

• 最小花费$s$

13

思路

由于我没有接触过旅行商问题的解法，所以第一时间是想到会的维特比算法，同样是在状态间跳转求极值，但与维特比算法不同的是，维特比算法在每一个时间点$t$可以取所有状态，而旅行商问题有一个每一个城市只去一次的约束，也就是每个在整个过程中每一个状态只能出现一次。他们两个都可以看成是一条条不同的路径，维特比算法的总路径数为$|c|^T$（|c|个状态，时间长度为$T$），旅行商问题总路径数为$|c|!$，$|c|$为中间城市数，对所有中间城市全排列。旅行商问题相当于维特比算法加了一个每个状态只能出现一次的约束。对于维特比算法的详细阐述和应用详见HMM部分。现尝试能否从维特比算法扩展得到旅行商问题的解法，维特比算法可表示为

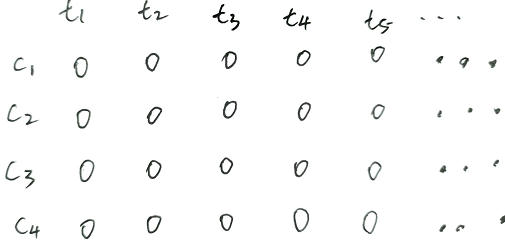
需要维护一个二维数组$F[t][c]$表示为$t$时刻状态为$c$的最小代价，其同样表示了从$[0, t]$时间段的一条最小路径，该路径$t$时刻的状态为$c$，并且其使代价最小，其更新公式为

$$F[t][c] = \underset{k}{\min}{\Large\{} F[t-1][k] + S[k][c] {\Large\}}$$ 其中$S[k][c]$表示状态$k$跳转到状态$c$的代价。
这里需要特别提一句的是$F[t][c]$不止代表了一个最小$\text{scalar}$，其还表征了一条从时刻$0$到时刻$t$的最小路径$[C^0, C^1, C^2, \cdots, C^{t-1}, C^t]$，并且$C^t = c$

到这里，旅行商问题开始出现不一样的地方，其要求每个状态只能出现一次$C^0 \neq C^1 \neq C^2 \neq \cdots \neq C^t$，现在需要做的是如何在更新状态的过程中保证该约束。

更新公式附加上该约束以数学形式写出来为

$$F[t][c] = \underset{k}{\min}{\Large \{} F[t-1][k]+ S[k][c] {\Large\}}, \quad c\notin L[t-1][k]$$ ，$L[t-1][k]$表示对应的最短路径状态序列，只需要保证当前$t$时刻的要更新的状态$c$不在更新公式的$t-1$时刻的最短路径状态序列中。当然$c\notin L[t][c], k\notin L[t-1][k]$

从公式可以看到，不需要关注整个全排列组成的状态路径，而只需要知道状态的集合即可，更新公式不直接与路径顺序有关，相当于用每个时间点的所有集合状态去更新去更新下一个时刻的状态。由此，根据全排列得到的路径求及值时可以用$DP$把庞大数量的全排列数转换成集合

那么状态更新可以表示成集合的形式，$F[S][c]$表示经过集合$S$状态到达$c$状态的最小代价，则其可以表征成终点是$c$把集合$S$全排列的所有路径中代价最小的路径。其实这一个转换是整个过程中最最最最重要的部分，其他的包括后面的状态压缩都可以看成是$\text{trick}$，而这一个转换是最难想的，前人能够想到真是优秀

现在看旅行商问题，$F[S][c]$表示从北京出发，经过城市集合$S$到城市$c$的最小代价，其更新公式为

$$F[S][c] = \underset{k}{\min{\Large\{}} F[S\setminus\{k\}][k] + S[k][c] {\Large\}}, \quad c\notin S, k \in S$$ 其中，$S\setminus\{k\}$表示从集合$S$中删掉$k$，更新中间城市为集合$S$目标城市为$c$的最小代价，只需要保证$F[S\setminus \{k\}][k]$是最小的就可以保证整个式子是对的，那么只需要保证更新顺序从小到大（城市数）依次更新即可，并且每次更新完当前集合的所有状态，例如更新完一个城市的再更新2个城市的再是三个城市的，，，，这样假设有$n$个中间城市，则总共的集合数为
$$\binom{n}{1} + \binom{n}{2} + \binom{n}{3} + \cdots + \binom{n}{n} = 2^n - 1$$

然后大佬们发现，可以用二进制表示每个城市在不在集合里面，这样一个集合就可以用一个二进制表示，并且该二进制表示的从小到大的顺序也符合上面状态更新要求的顺序，例如有$5$个城市的二进制集合状态为$01011$，更新时抽取的中间城市$k$需要在集合里面，故筛掉$k$的所有集合为$00011, 01001, 01010$，其肯定满足$01011$比其他的都要大，因为相当于用1个0替换掉$01011$中的一个1，得到的值肯定比$01011$小，更新$01011$的状态需要让$00011, 01001, 01010$的状态已经是最优的，由于在二进制顺序中他们都要比$01011$小已经被更新过，所以成立，这就是状态压缩

判断$c$不在状态集合$S$里面：!(S & (1<<c))
判断$k$在状态集合$S$里面：S & (1<<k)
$S\setminus\{k\}$：S ^ (1<<k)

代码

#include <stdio.h>
#include <string.h>
const int MAXN = 20 + 1;
const int MAXS = 1000 + 1;
int F[1 << (MAXN - 1)][MAXN];
int S[MAXN][MAXN];
int _min(int a, int b);
int main() {
    memset(F, 0x00, sizeof(F));
    memset(S, 0x00, sizeof(S));
    int n, s;
    scanf("%d", &n);
    for(int i=0; i<n; i++) {
        for(int j=0; j<n; j++) {
            scanf("%d", &s);
            S[i][j] = s;
        }
    }
    int maxn = (1 << n) - 1;
    for(int i=1; i<=maxn; i++) {
        for(int c=0; c<n; c++) {
            F[i][c] = MAXS;
        }
    }
    for(int c=0; c<n; c++) {
        F[0][c] = S[0][c];
    }
    int iters = 0;
    for(int state=1; state<=maxn; state++) {
        for(int c=0; c<n; c++) {
            // c must not in state
            if(!(state & (1<<c))) {
                for(int k=1; k<n; k++) {
                    // k must in state
                    if((state & (1<<k))){
                        // delete k in state with xor
                        int current = state ^ (1<<k);
                        F[state][c] = _min(F[state][c], F[current][k] + S[k][c]);
                        iters += 1;
                    }
                }
            }
        }
    }
    // print for debug
    printf("<< F >>\n");
    for(int state=0; state<=maxn; state++){
        for(int c=0; c<n; c++){
            printf("%d \t", F[state][c]);
        }
        printf("\n");
    }
    printf("<< F - End >>\n");
    //
    printf("%d\n", F[maxn-1][0]);
    //
    printf("Iters: %d", iters);
}
int _min(int a, int b){
    return a < b ? a : b;
}
/*
4
0 2 6 5
2 0 4 4
6 4 0 2
5 4 2 0
*/

输出

4
0 2 6 5
2 0 4 4
6 4 0 2
5 4 2 0
<< F >>
0       2       6       5
1001    1001    1001    1001
4       1001    1001    1001
1001    1001    1001    1001
12      1001    1001    1001
1001    1001    1001    1001
1001    1001    1001    1001
1001    1001    1001    1001
10      1001    1001    1001
1001    1001    1001    1001
1001    1001    1001    1001
1001    1001    1001    1001
1001    1001    1001    1001
1001    1001    1001    1001
1001    1001    1001    1001
1001    1001    1001    1001
<< F - End >>
1001
Iters: 36

优化

上面状态$S$包含了北京，而$S$只需要是中间城市即可

#include <stdio.h>
#include <string.h>
const int MAXN = 20 + 1;
const int MAXS = 1000 + 1;
int F[1 << (MAXN - 1)][MAXN];
int S[MAXN][MAXN];
int _min(int a, int b);
int main(){
    memset(F, 0x00, sizeof(F));
    memset(S, 0x00, sizeof(S));
    int n, s;
    scanf("%d", &n);
    for(int i=0; i<n; i++){
        for(int j=0; j<n; j++){
            scanf("%d", &s);
            S[i][j] = s;
        }
    }
    int maxn = (1 << (n - 1)) - 1;
    for(int i=1; i<maxn; i++){
        for(int c=0; c<n-1; c++){
            F[i][c] = MAXS;
        }
    }
    for(int c=0; c<n-1; c++){
        F[0][c] = S[0][c + 1];
    }
    int iters = 0;
    for(int state=1; state<maxn; state++){
        for(int c=0; c<n-1; c++){
            // c must not in state
            if(!(state & (1<<c))){
               for(int k=0; k<n-1; k++){
                    // k must in state
                    if(state & (1<<k)){
                        // delete k in state with xor
                        int current = state ^ (1<<k);
                        F[state][c] = _min(F[state][c], F[current][k] + S[k+1][c+1]);
                        iters += 1;
                    }
                }
            }
        }
    }
    int res = MAXS;
    for(int k=0; k<n-1; k++){
        int c = maxn ^ (1<<k);
        res = _min(res, F[c][k] + S[k+1][0]);
        iters += 1;
    }
    // print for debug
    printf("<< F >>\n");
    for(int state=0; state<maxn; state++){
        for(int c=0; c<n-1; c++){
            printf("%d \t", F[state][c]);
        }
        printf("\n");
    }
    printf("<< F - End >>\n");
    //
    printf("%d\n", res);
    //
    printf("Iters: %d\n", iters);
}
int _min(int a, int b){
    return a < b ? a : b;
}
/*
4
0 2 6 5
2 0 4 4
6 4 0 2
5 4 2 0
*/

输出

4
0 2 6 5
2 0 4 4
6 4 0 2
5 4 2 0
<< F >>
2       6       5
1001    6       6
10      1001    8
1001    1001    8
9       7       1001
1001    8       1001
11      1001    1001
<< F - End >>
13
Iters: 15