Number of Islands

LintCode LeetCode

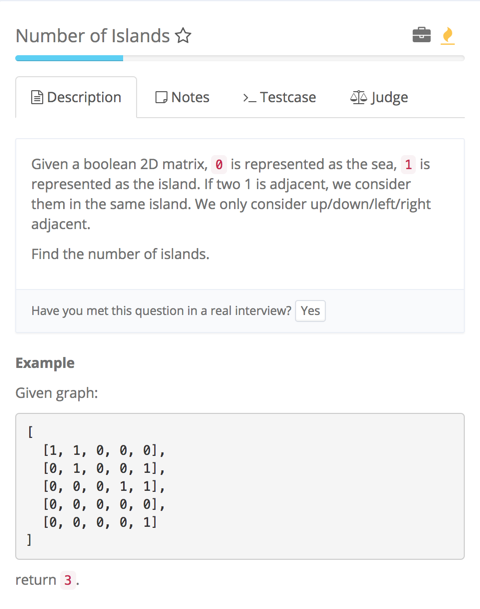
这道题是BFS in matrix这一类问题，用到了Flood fill的方法。所有标记为1的点为岛屿，岛屿于上下左右的岛屿相通。
我们用两个for循环遍历整个矩阵，找到是岛屿的点，对其进行markByBFS,也就是对它周围上下左右的点进行检测标记。同时岛屿数加一，最后统计进行了markByBFS的次数，也就得到岛屿数目。

BFS部分跟在graph上基本一样，区别在于检测某个岛屿它上下左右的方块时，由于没有neighbors这个属性，需要通过坐标变换数组进行操作。坐标变换数组不唯一，只需要满足能遍历上下左右四个点就可以。在这个过程中，用一个inBound方法来限制我们遍历的范围不会越界。

自己画一下queue的offer和poll就很好理解Flood fill在这道题的运用。当我们发现第一个1时，立马将其标记为0，加入队列；当我们poll出刚才找到的那个点时，我们在它的上下左右找也是1的点，找到之后也标记为0，并加入队列。这种将原来是1的点Mark为0，并且像灌水一样将连着的都是1的点都mark为0的过程就是灌水法，很具体形象。

class Coordinate{
    public int x;
    public int y;
    public Coordinate(int x, int y){
        this.x = x;
        this.y = y;
    }
}
public class Solution {
    /**
     * @param grid a boolean 2D matrix
     * @return an integer
     */
    public int numIslands(boolean[][] grid) {
        // Write your code here
        if (grid == null || grid.length == 0 || grid[0].length == 0){
            return 0;
        }
        int m = grid.length;
        int n = grid[0].length;
        int numOfIslands = 0;
        for (int i = 0; i < m; i ++){
            for (int j = 0 ; j < n; j++){
                if (grid[i][j] == true){
                    markByBFS(grid,i, j);
                    numOfIslands += 1;
                }
            }
        }
        return numOfIslands;
    }
    private void markByBFS(boolean[][] grid,int x, int y){
        int [] deltaX = {1,0,0,-1};
        int [] deltaY = {0,1,-1,0};
        Queue<Coordinate> queue = new LinkedList<Coordinate>();
        grid[x][y] = false;
        queue.offer(new Coordinate(x,y));
        while (!queue.isEmpty()){
            Coordinate coor = queue.poll();
            for (int i = 0; i < 4; i ++){
                Coordinate adj = new Coordinate(coor.x + deltaX[i], coor.y + deltaY[i]);
                if (!inBound(grid,adj.x,adj.y)){
                    continue;
                }
                if (grid[adj.x][adj.y] == true){
                    grid[adj.x][adj.y] = false;
                    queue.offer(adj);
                }
            }
        }
    }
    private boolean inBound(boolean[][] grid, int x, int y){
      if ( x >= 0 && x < grid.length && y >= 0 && y < grid[0].length){
          return true;
      }  
      return false;
    }    
}