Disjoint Sets Study Guide

CS61B

Review

Dynamic Connectivity Problem

这一届主要讲动态连接问题，目的是要得到一种data type，它可以使得固定数量N个对象支持下列操作：

• connect
• isConnected

Quick Find

connect的runtime是Θ（N），因为connect(p,q)的时候，不只是要把p的id变成q的id,而是要把任何id跟p的id相等的所有元素的id变为q的id，以为这需要iterate over the entire array：

Quick Union

Quick Union改变了id[]的含义，现在id[i]代表i的parent，find会找到某个对象最上端的根；现在要connect两个对象，只需要将前一个对象的根连接到后一个对象的根下，就只需one change to id[]：

虽然现在connect只require one change to id[]，但是root finding却可能需要爬整个tree，所以connect的worst case是是Θ（N）：

WeightedQuickUnion

WeightedQuickUnion相比QuickUnion,connect(p,q)时 不是把前一个元素的根连接到后一个元素的根下方，而是把smaller tree的root连接到bigger tree的root下方（这里的small指的是该tree的元素少，而不是深度少）；
这样的情况下，树高为lgN, 所以root finding的时候worst case需要O(lgN)：

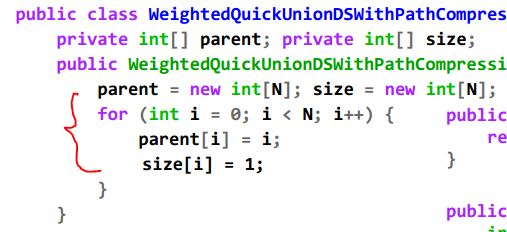
WeightedQuickUnionWithPathCompression:

Path Compression即在find()被call时，每一个along the way的node都会指向root：

log*(N) 即Log star N, 最多为5，所以相对来说runtime减小了不少

比较：

Recommended Problems

B level
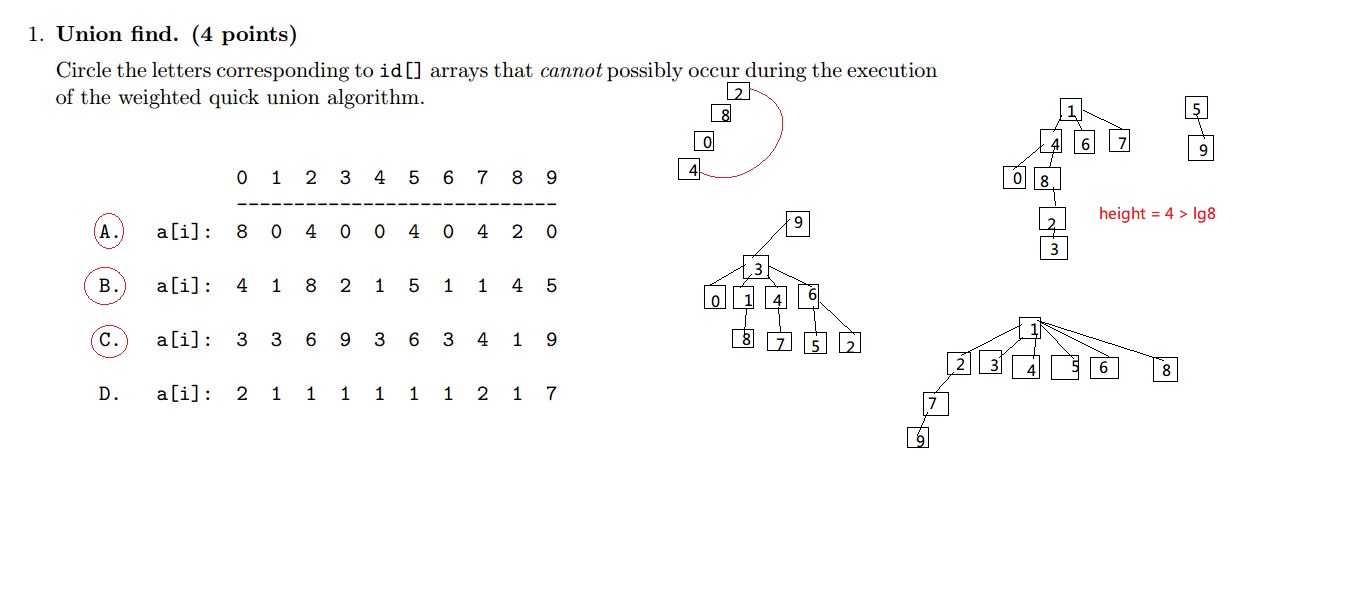
Problem 1 from the Princeton Fall 2011 midterm.

注意要满足height < lgN, height是从顶端到末段元素数量-1；
B项也重要，注意到0位parent的一分支比9为parent的另一分支size大（元素多），那0作parent的分支是不可能连接到9之下的；同时也可以根据0的Parent 9所在树的size应该至少double0作parent所在树的size来判断这里不满足条件

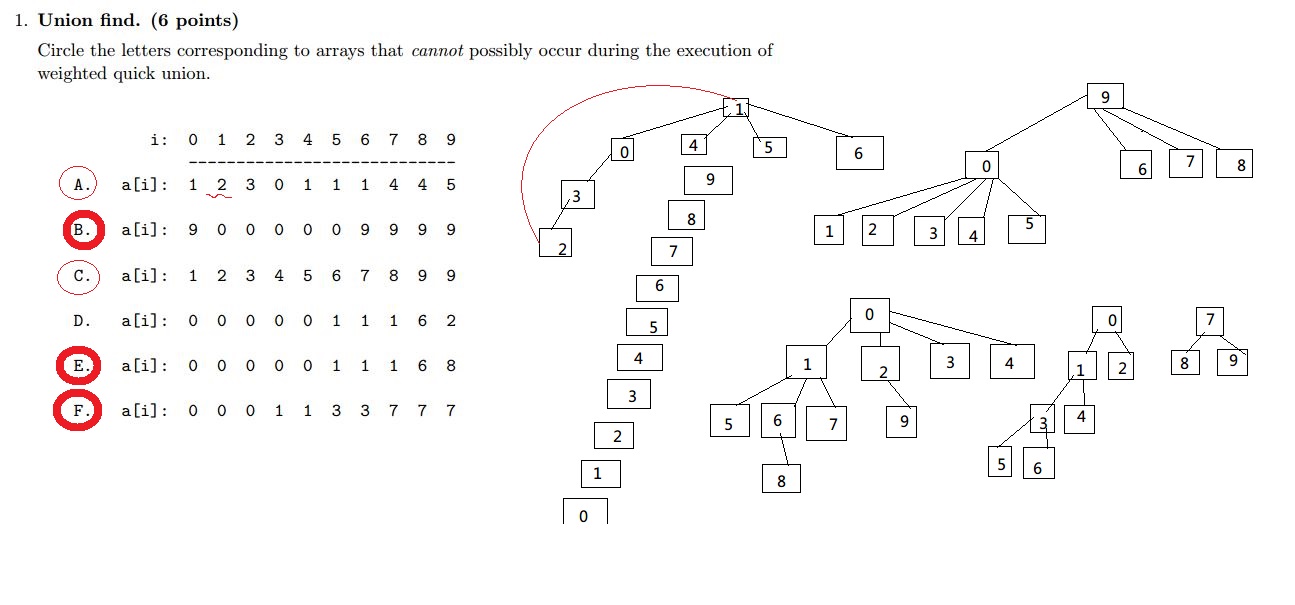
Problem 1 from the Princeton Fall 2012 midterm.

C项比较重要，wighted quick union有一条标准：
The size of the tree at least doubles since weight(T2) ≥ weight(T1)
但这里3的parent9所拥有的元素数目只比3多1，没有3的两倍：

答案：

3.

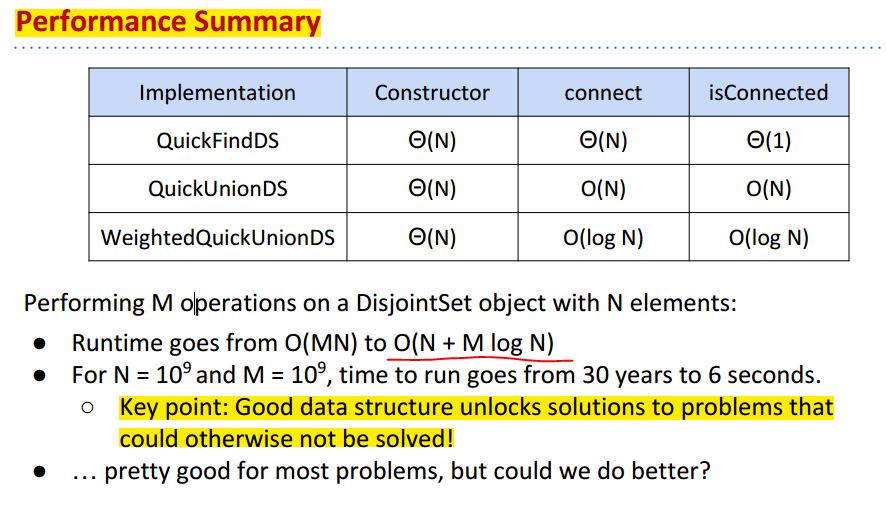
课上的slide讲到weighted quick union的runtime：

runtime包括了Union和isConnected操作，但不要忘了还有array creation需要的runtime：

array creation:

5.

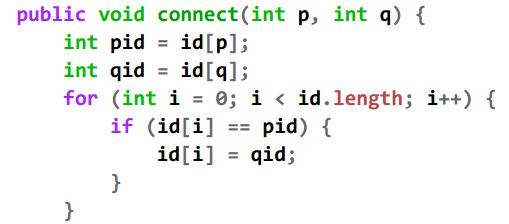
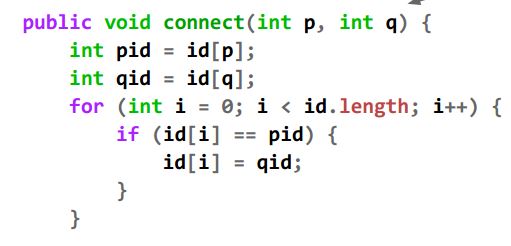
这道题乍看上去没毛病，但我们看一看Quick Find在课程slides里的实施：

正确实施多了两行code：

int pid = id[p];
int qid = id[q];

而在上面的直觉实施里，面临着一个问题：即id[p]在for loop里被变为id[q],当存在r>p的id[r] = id[p]时，它就不会被改变成id[q]了

A LEVEL 3

public class weightedQUwithPC{
    int [] parent;
    int [] size;
    public weightedQUwithPC(int N) {
        parent = new int[N];
        size = new int[N];
        for(int i = 0; i< parent.length; i++){
            parent[i] = i;
            size[i] = 1;
        }
    } 
    public void union(int p, int q) {
        int i = find[p];
        int j = find[q];
        if(i == j){
          return;
        }
        if(size[i] > size[j]){
            parent[j] = i;
            size[i] += size[j];
        }else {
            parent[i] = j;
            size[j] += size[i];
        }
    }
    public int find(int p) {
        if ( parent[p] == p) {
            return p;
        }
        while(! parent[p] == p){
            p = parent[p]
        }
        return p;
    }
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }
}

find()写的有问题，参考slide: