Lecture 20: Disjoint Sets

CS61B

Quick Find

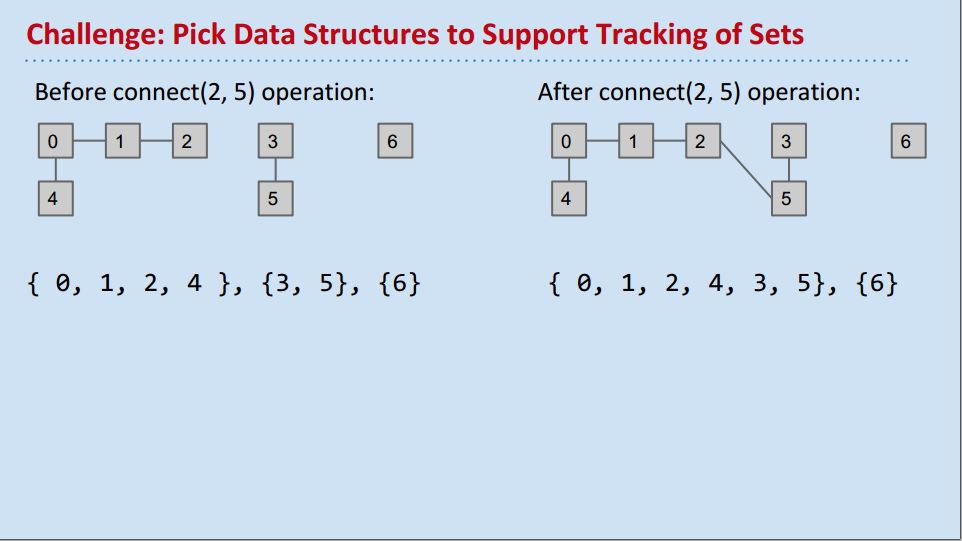
选择一种data structure来表达Sets：

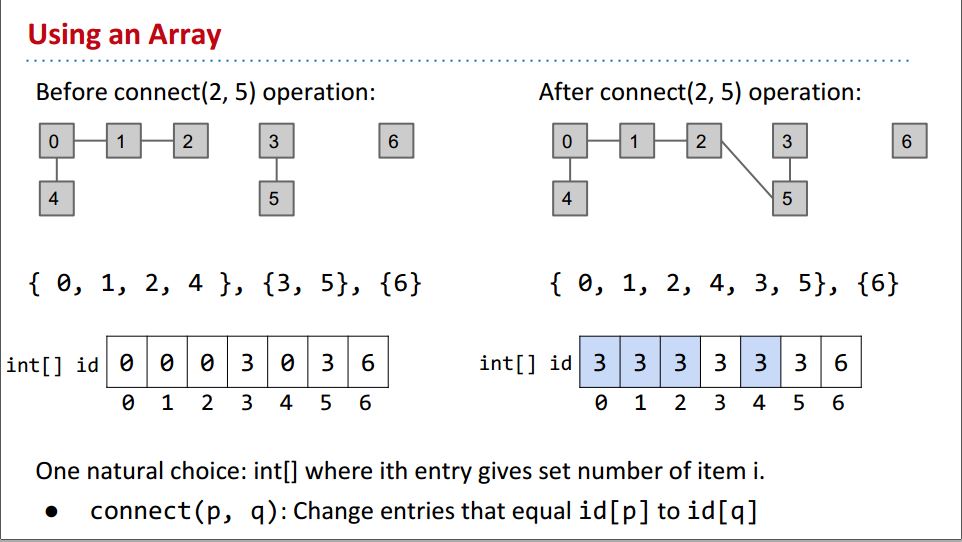
我们用Array:

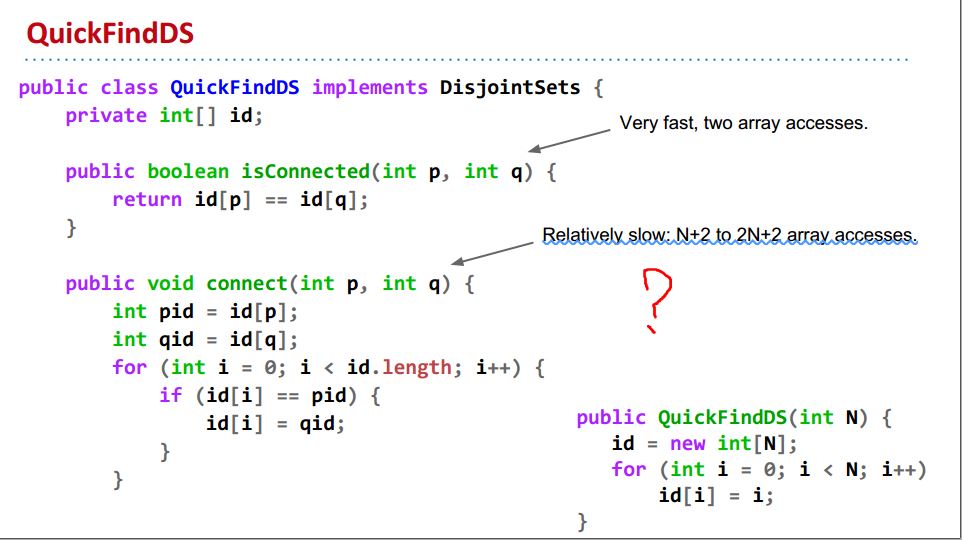
具体的实施：为什么这儿是N+2到2N+2次array access呢？这里注意一下array access指的是什么

最坏情况是if语句都判断为真，那么if语句算一次access,另一句赋值算一次access;而最好情况是if语句都判断为false,那么就只有if语句这一次access，再加上上面的2次access，所以一共有N+2 ~ 2N+2次array access:

Runtime:

Quick Union

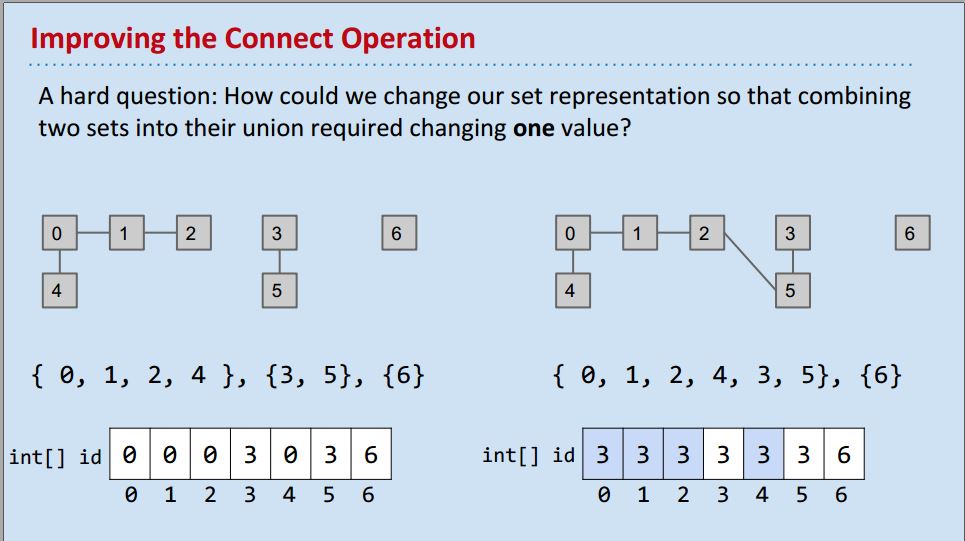
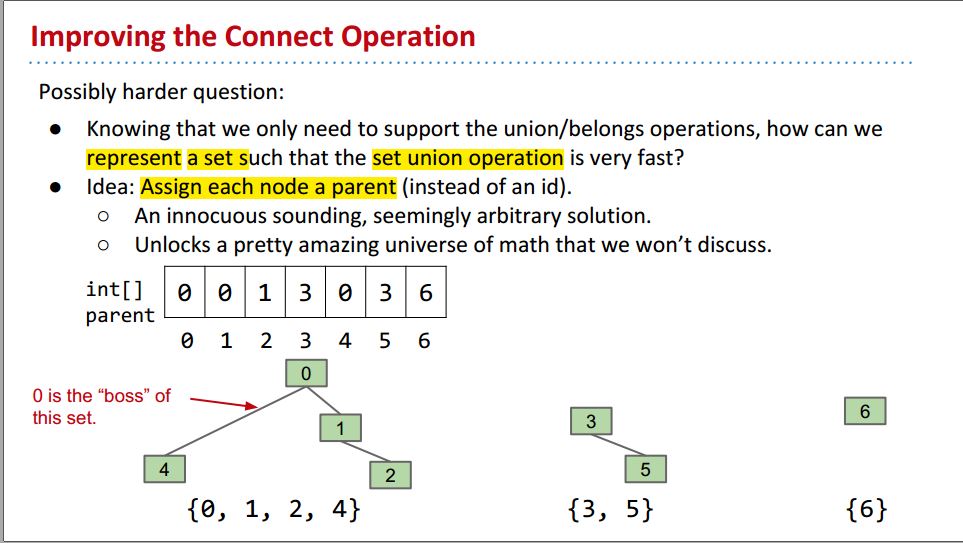
现在我们想提高Connect操作的效率，那么我们该如何调整set的表示方法，能够使得connect两个sets只需要改变一个值？

现在我们不用id[],而是给每个node一个parent:

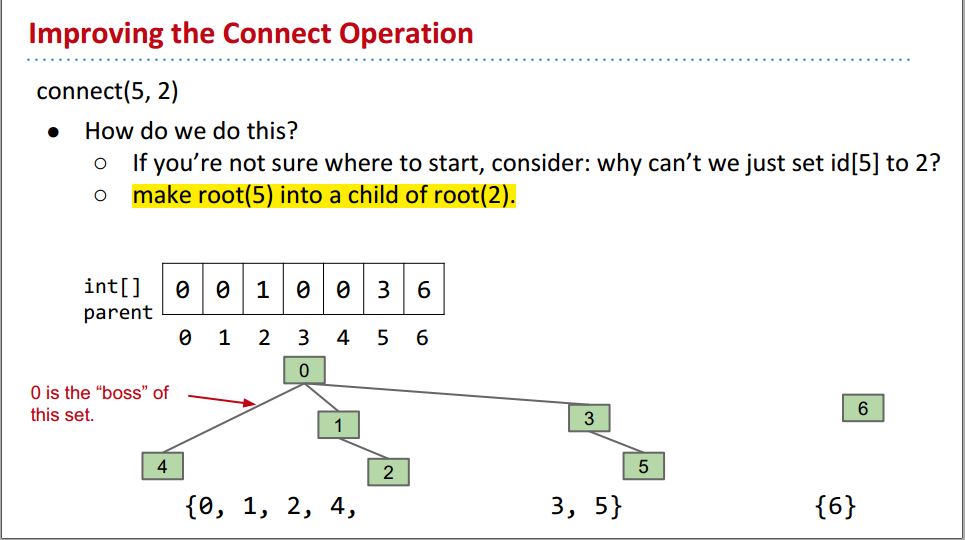
比如现在我们要connect（5，2），我们就前一个数字的根变为后一个数字的根的子分枝：

这种方法存在一种问题，树可能变得很长很长：

具体实施：

Performance:
因为这里的find（）的worst case其实是O（N），（worst case下的big theta又是Θ（N）），所以相应的connect(里面有find（））是O（N），isConnected()也是O（N）；

Weighted Quick Union

改进一下Quick Union来避免tall trees：

最少需要改变：

• 还是用之前的parent[]数组，但是要新增加一个size[]；
• isConnected没变化
• connect（）需要两处变化：
  
  • 把较小树的根连接到较大树的根
  • 更新size[]数组

Weighted Quick Union Performance:

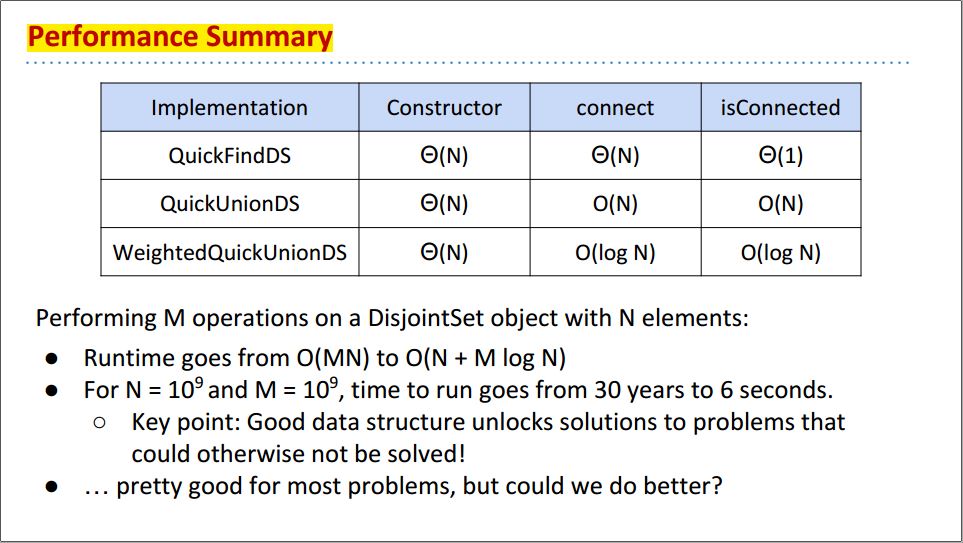
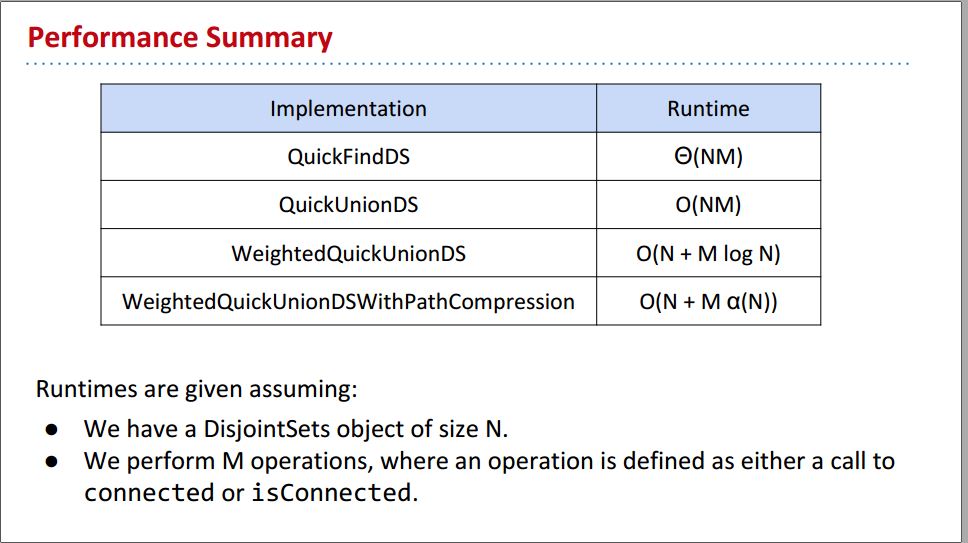
Performance Summary:

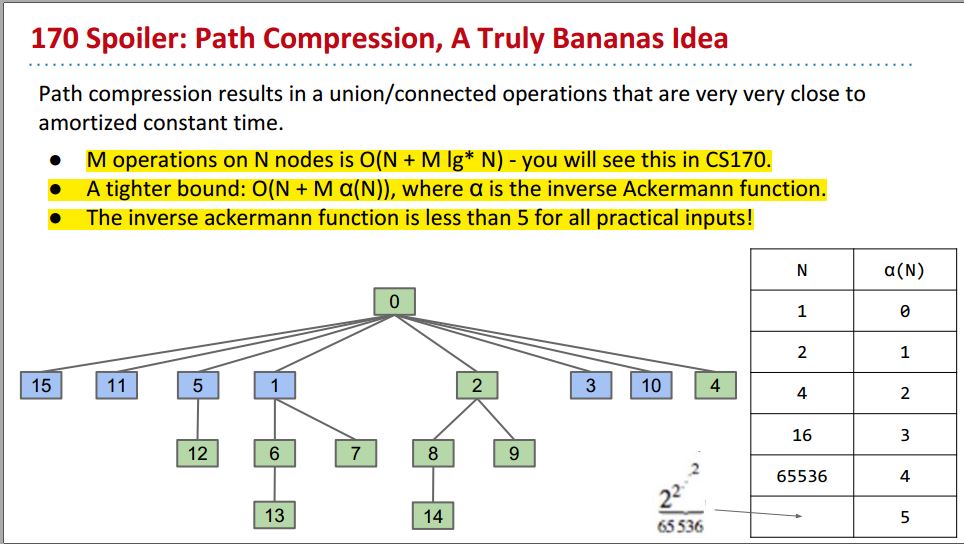
Path Compression

要判断isConnected()的时候，将两个Node所在的分支中每一个Node都改为直接跟root相连:

这样的话，N个Nodes上M次操作需要 O（N + Mlg*N)； lg*N最多不会超过5，这个值约等于O（N+M)；
α（N）：Ackermann function

改变后的find（）：

代码：

Performance分析：