Topological Sorting

LintCode

该视频帮助理解 ：
Topological Sort

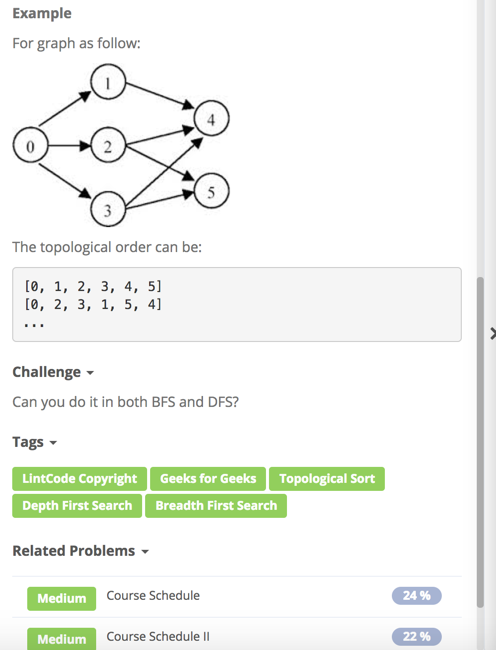
Topological sorting被老师称为“非常重要”，据说每家公司面试都会考到。Topological order的定义是：
1、图上u->v则排序后u点一定在v点前面
2、排序后的开头的点必须是没有指向该点的edge.(indegree == 0)

In this problem, we use a HashMap to map all nodes to their indegree. By traversing each node's neighbors and put them in the map, those nodes with indegree 0 have been left. We offer these nodes with 0 indegree to the queue and add them to the result.Then we start with these nodes to sort in topological order. We poll one node each time, meaning we traversed it and delete it from the graph. Meanwhile we minus the indegree of its neighbors by one, meaning we delete the edges between this node to its neighbors. We'll then check if any of its neighbors have an indegree of 0, if so we add it to the result and poll it to the queue. We'll later poll it out from the queue and check its neighbors.

This is BFS method, the only difference is that we'll need to check the indegree when we offer a node to the queue.

/**
 * Definition for Directed graph.
 * class DirectedGraphNode {
 *     int label;
 *     ArrayList<DirectedGraphNode> neighbors;
 *     DirectedGraphNode(int x) { label = x; neighbors = new ArrayList<DirectedGraphNode>(); }
 * };
 */
public class Solution {
    /**
     * @param graph: A list of Directed graph node
     * @return: Any topological order for the given graph.
     */    
    public ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
        // write your code here
        ArrayList<DirectedGraphNode> result = new ArrayList<>();
        if (graph == null || graph.size() == 0) {
            return result;
        }
        Map<DirectedGraphNode, Integer> indegree = new HashMap<DirectedGraphNode, Integer>();
        Queue<DirectedGraphNode> queue = new LinkedList<DirectedGraphNode>();
        //mapping node to its indegree to the HashMap, however these nodes
        //have to be directed to by one other node, nodes whose indegree == 0
        //would not be mapped.
        for (DirectedGraphNode DAGNode : graph){
            for (DirectedGraphNode nei : DAGNode.neighbors){
                if(indegree.containsKey(nei)){
                    indegree.put(nei, indegree.get(nei) + 1);
                } else {
                    indegree.put(nei, 1);
                }
            }
        }
        //find all nodes with indegree == 0. They should be at starting positon in the result
        for (DirectedGraphNode GraphNode : graph) {
            if (!indegree.containsKey(GraphNode)){
                queue.offer(GraphNode);
                result.add(GraphNode);
            }
        }
        //everytime we poll out a node from the queue, it means we delete it from the 
        //graph, we will minus its neighbors indegree by one, this is the same meaning 
        //as we delete the edge from the node to its neighbors.
        while (!queue.isEmpty()) {
            DirectedGraphNode temp = queue.poll();
            for (DirectedGraphNode neighbor : temp.neighbors){
                indegree.put(neighbor, indegree.get(neighbor) - 1);
                if (indegree.get(neighbor) == 0){
                    result.add(neighbor);
                    queue.offer(neighbor);
                }
            }
        }
        return result;
    }
}