Lecture 23: Hashing

CS61B

Set Implementations, DataIndexedIntegerSet

先讲Techniques for Storing Data，这里讲了三种方式：
- LinkedList
- Bushy BST
- Unordered Array

他们都有一些Limitations, 比如Bushy BST:
● Items must be comparable.
● Maintaining bushiness is non-trivial.
● Θ(log N), can we do better?

而Ordered Array也没有好到哪里去，于是就引出了the third type of Array :
Using data as an Index

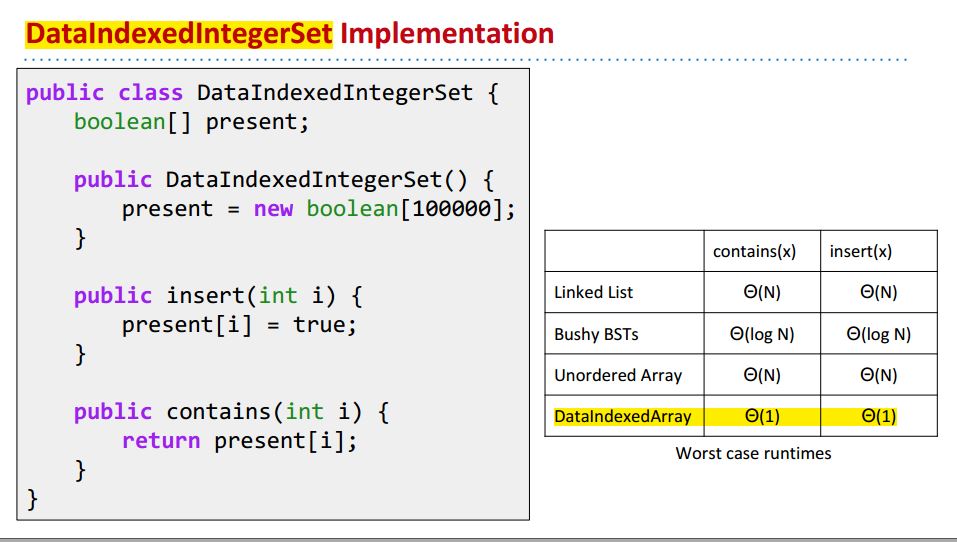
● Use data itself as an array index.
● Store true and false in the array.

DataIndexedIntegerSet Implementation:

Binary Representations, DataIndexedSet

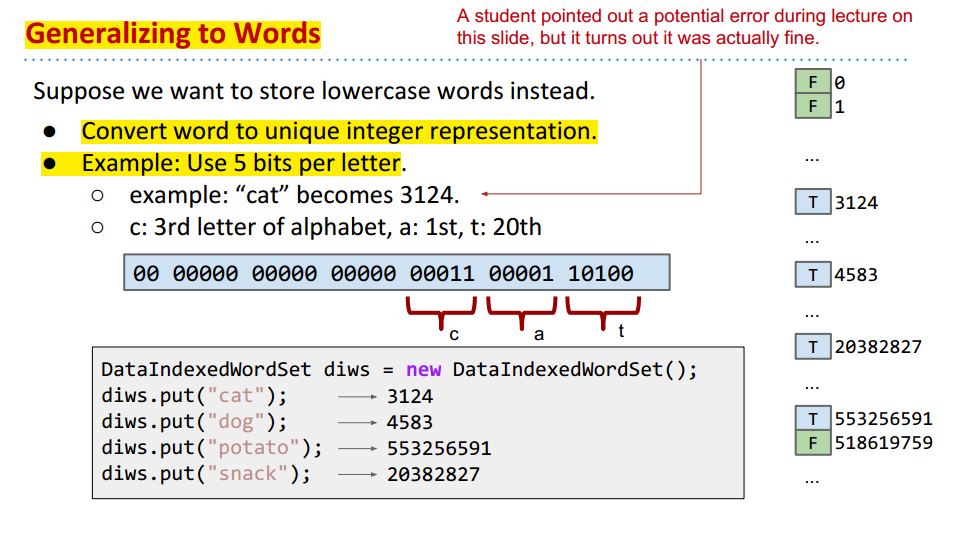
接下来讲二进制表示法来表示DataIndexedSet, 这里我们的data不再是Integer, 而是其他的比如lowercase words：

这里我们按照每个字母在字母表里的顺序来表示单词，比如cat, 我们用3124表示。为什么用32bits表示呢？因为Java里面Integer是32bits，所以用32位。

但这种表示方法存在局限性，当string过长，就没办法表示了；还可能出现不同的单词被表示成相同的整数，因为他们的高位有相同的部分，而最高位因为超过了32位直接被忽略了。

先不管这个Ambiguity问题，我们要记住DataIndexedWordSet Implementation里面有一个很重要的convertToInt方法， 用来将String表示成int. 它的具体实施方法并不重要。

总的来说，DataIndexedArray有两个挑战：

• 怎么处理Ambiguity，即collision handling.
• 到底怎么把String转换成int来表示，即computing a hashcode。

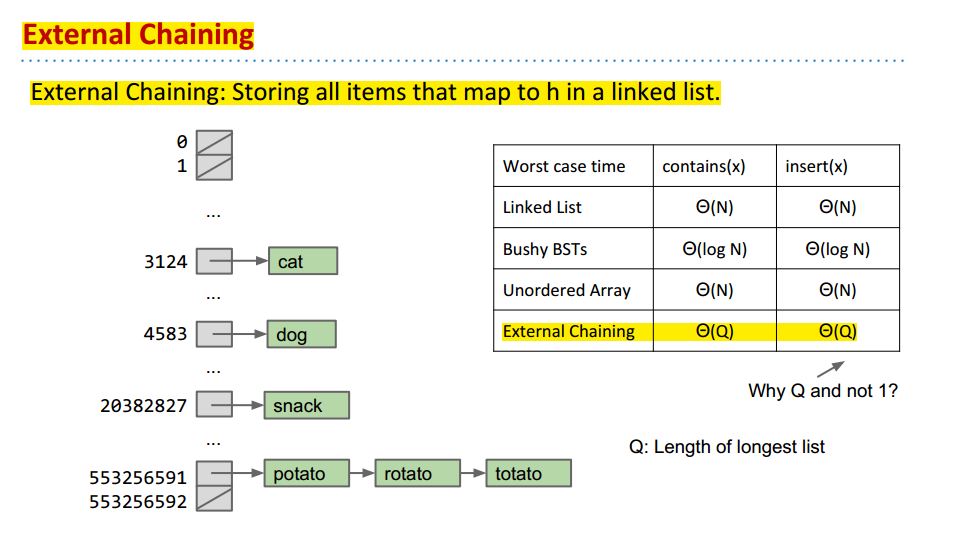
Handling Collisions

为了解决不同的N个items可能有相同的hashcode h的问题，我们不再在h处储存true, 取而代之我们储存包含N个items的List在h处。最简单的方法是LinkedList:

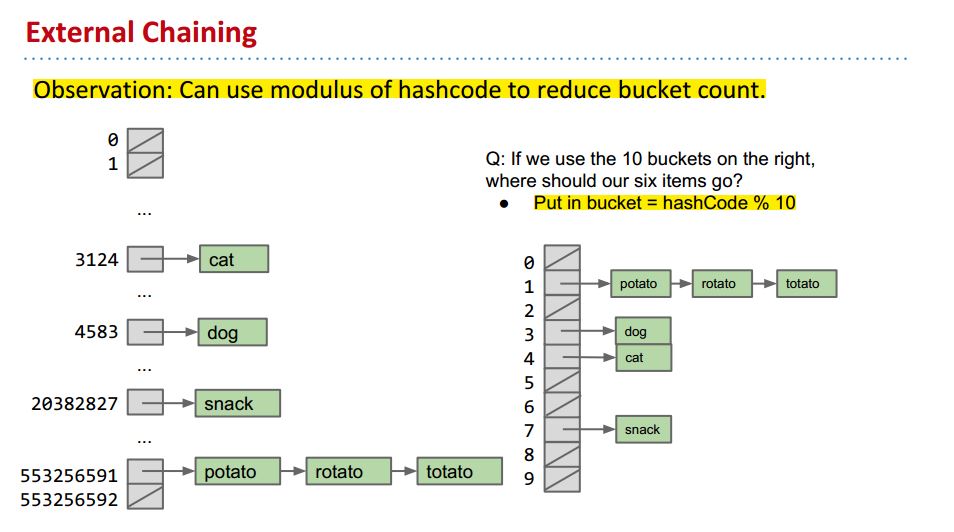
为了减少bucket的数目，我们可以取hashcode对bucket数目的模来储存items:

这种External Chaining的表现取决于load factor：
If N items are distributed across M buckets, average time grows with
N/M = L, also known as the load factor.

• Average runtime is Θ(L).

当load factor L很小的时候，可以看出这种数据结构很快。但当Items的数目N逐渐增长时，如何确保L保持较小呢？

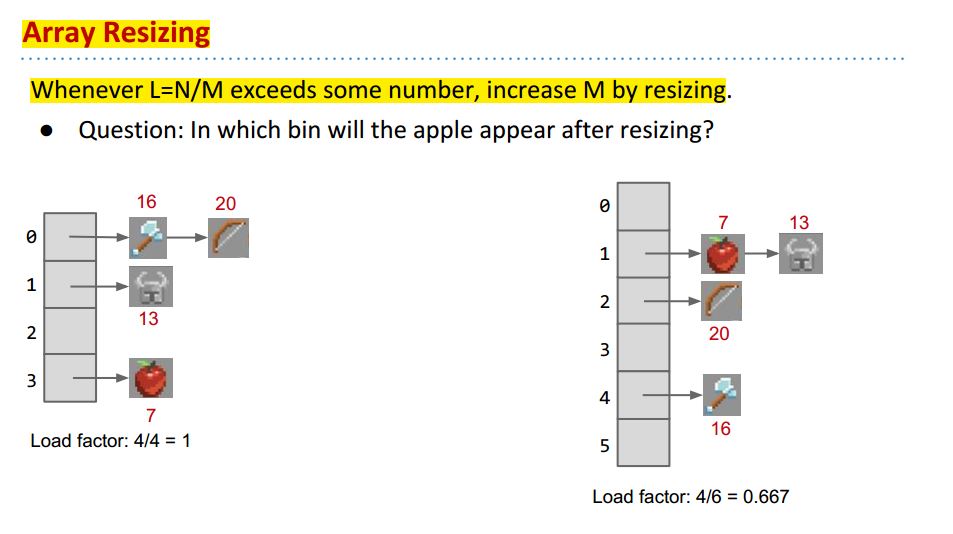
答案是Array Resizeing, 当N增大时，我们要增大M来确保L = N/M保持较小：

当hashcode是负数的时候要注意，直接取模可能会得到负数的Index，会报错ArrayIndexOutOfBoundsException,所以它的算法要特别处理。

比如这里hashcode是-1，但我们把它放在bucket 3. 而如果我们直接用 -1%4 来计算，我们会得到-1， 会报出异常，要留意这种特殊情况。

这种数据结构就是HashTable:

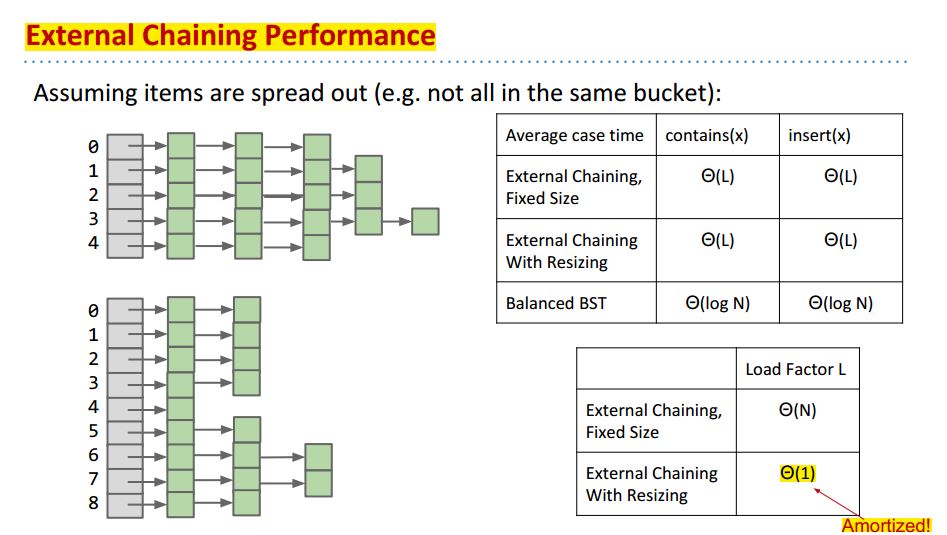
不同的External Chaining的Performance比较：

fixed size和 resizing array的runtime都是Θ（L），但fixed size里面L 是由Items数目决定的，表示为Θ（N）；而在resizing array里L是constant的，即我们可以令L = N/M为常数，当N增长时，resizing使得M增长，表示为Θ（1）.

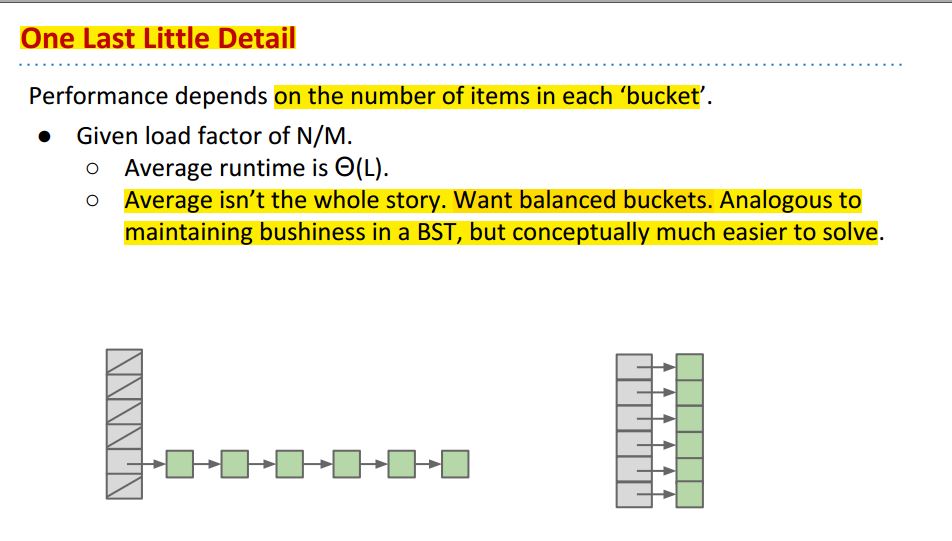
还要注意，类比于Bushy BST，我们也想要balanced buckets：

Hash Functions

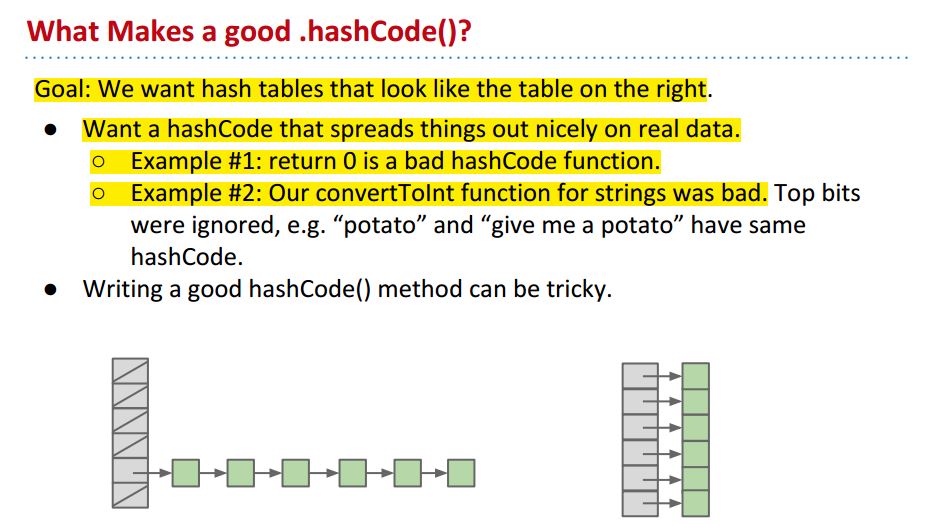
我们想要图中右边的hash table, 想要避免两种情况：

• 所有的hashcode都返回0，这将导致左边的情况，全部的items挤在一个bucket里；
• convertToInt方法完全忽略掉高位的bits.

改进后的hashCode（） funciton 可以解决只能表示Lowercase words的局限，通过乘以31的次幂来解决高位被忽略（这里不是很懂为啥）

这是一个hashCode()的例子：

hash这个词的意思是：
n.剁碎的食物；混杂，拼凑；重新表述
vt. 搞糟，把…弄乱；切细；推敲

来一个形象的感性认识：

Example: Hashing a Collection：

Example: Hashing a Recursive Data Structure

上面这两个例子看不大懂

Default hashCode（）返回的是地址，但很多时候你需要重写：

总结，当hashcode很好（就是之前一幅图右边那种）以及可以resizing的情况下，runtime是Θ（1）：

with resizing array, load factor是constant, 所以最多需要遍历L=N/M个items就可以得到contains()，以及insert().所以是constant time. big theta 1.