Lecture 30: Graphs IV: Minimum Spanning Trees

CS61B

MST, Cut Property, Generic MST Algorithm

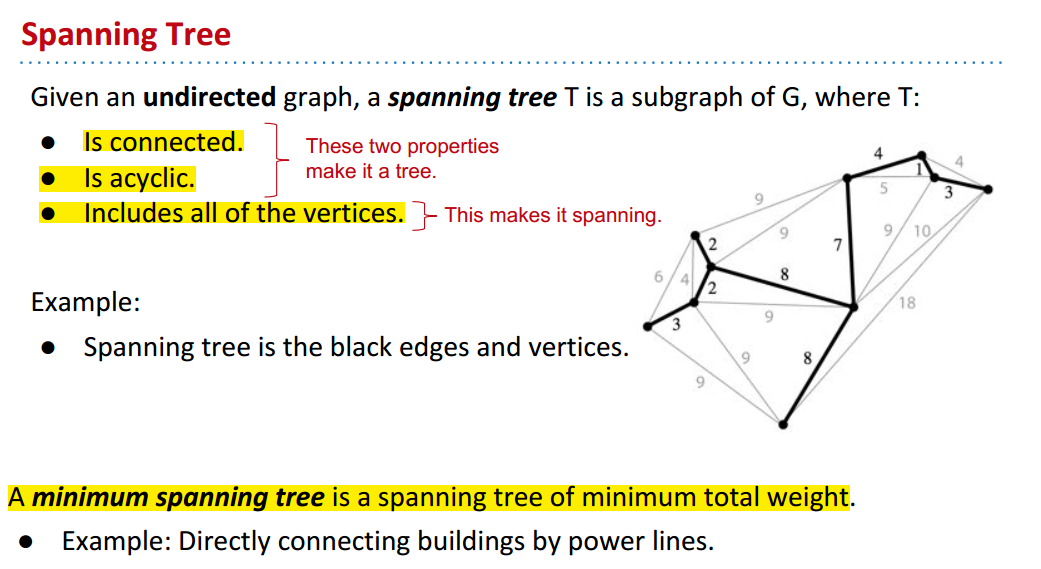
MST:

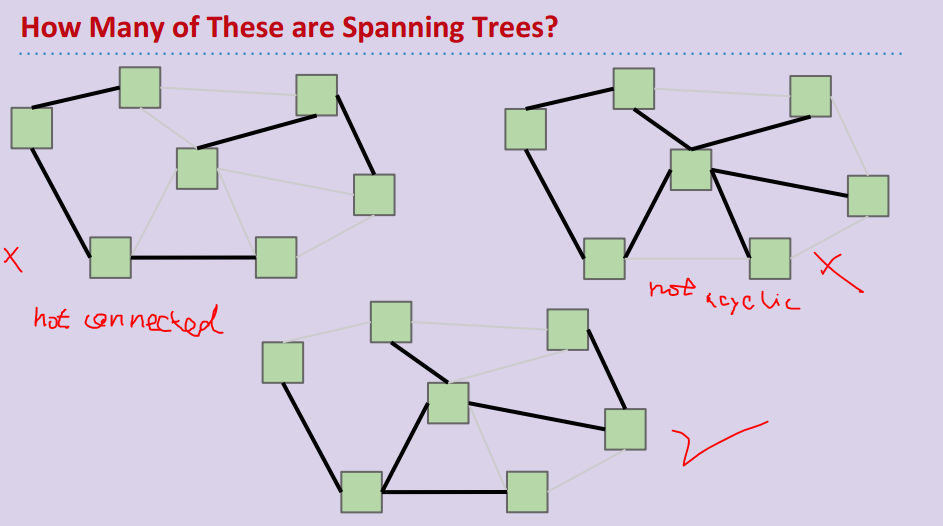
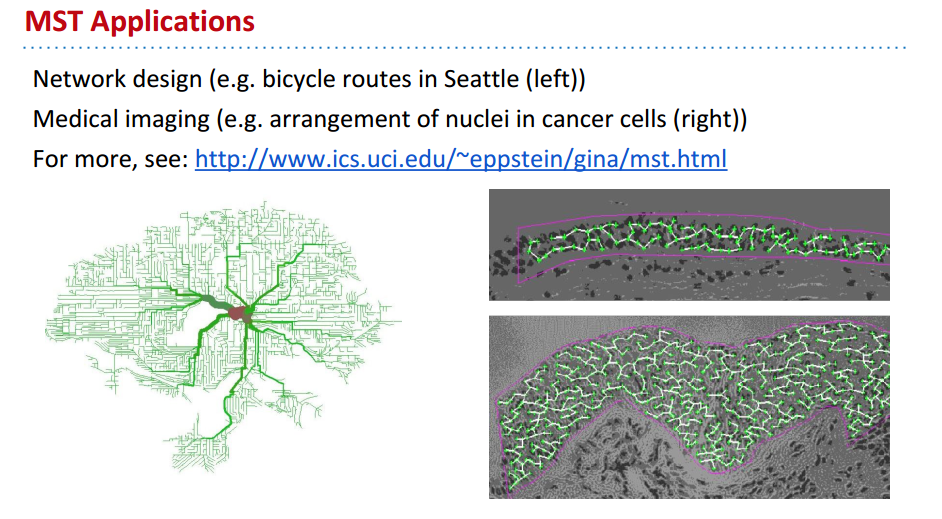
MST applications:

MST VS SPT

Cut property:

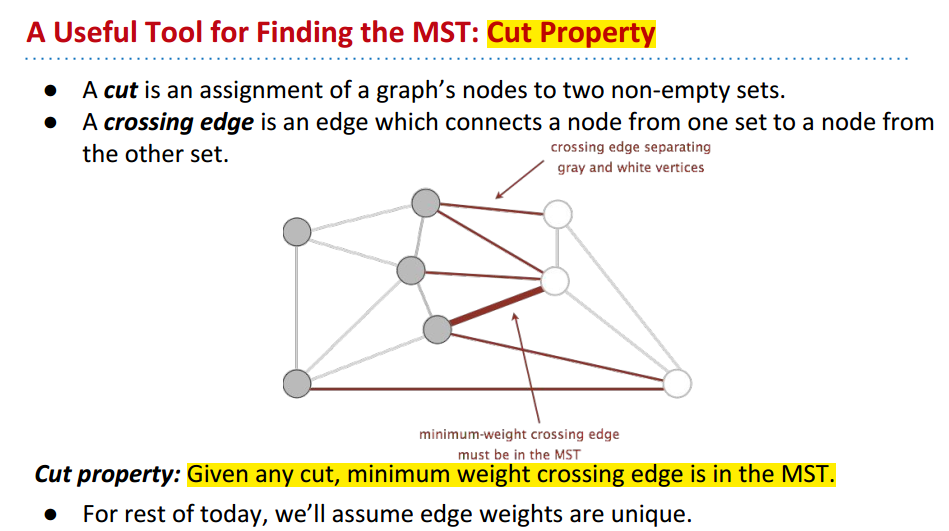
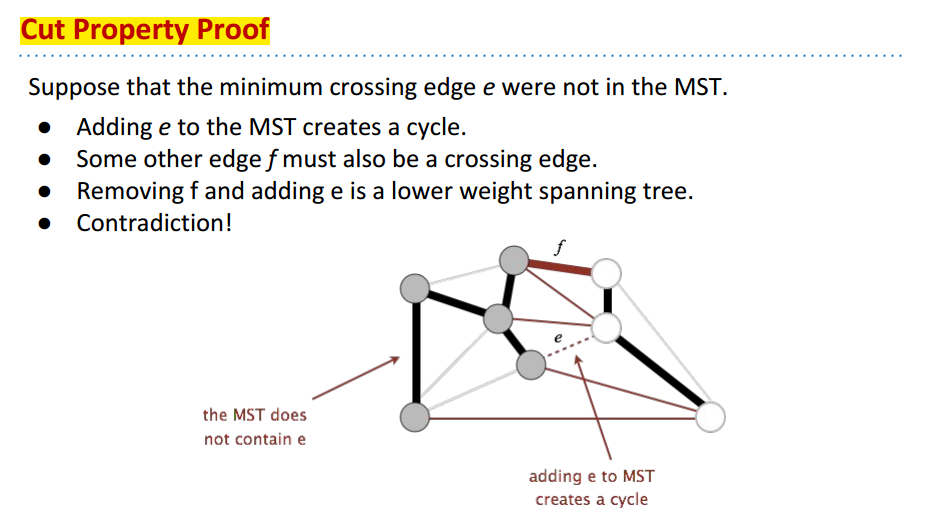
Cut property proof:

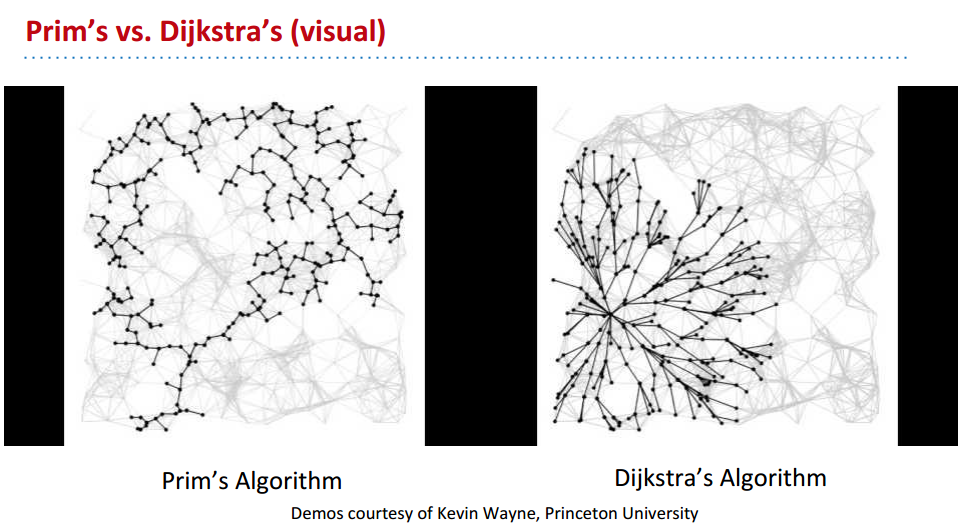
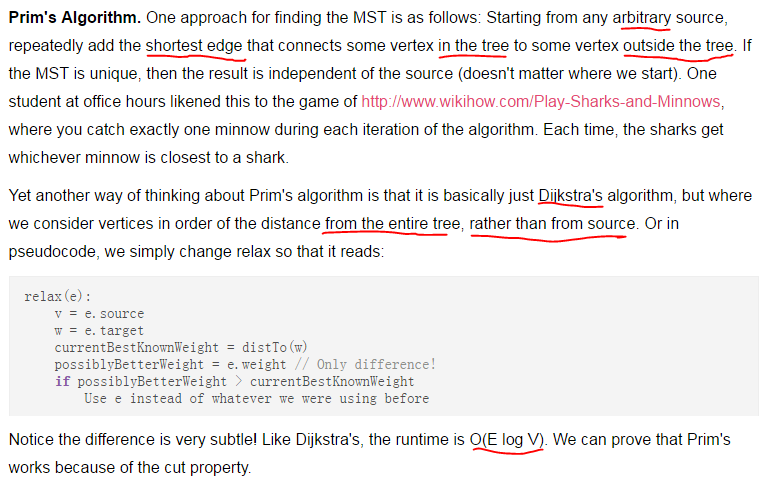
Prim’s Algorithm

Demo

Pseudocode:

Runtime:

Kruskal’s Algorithm

Demo

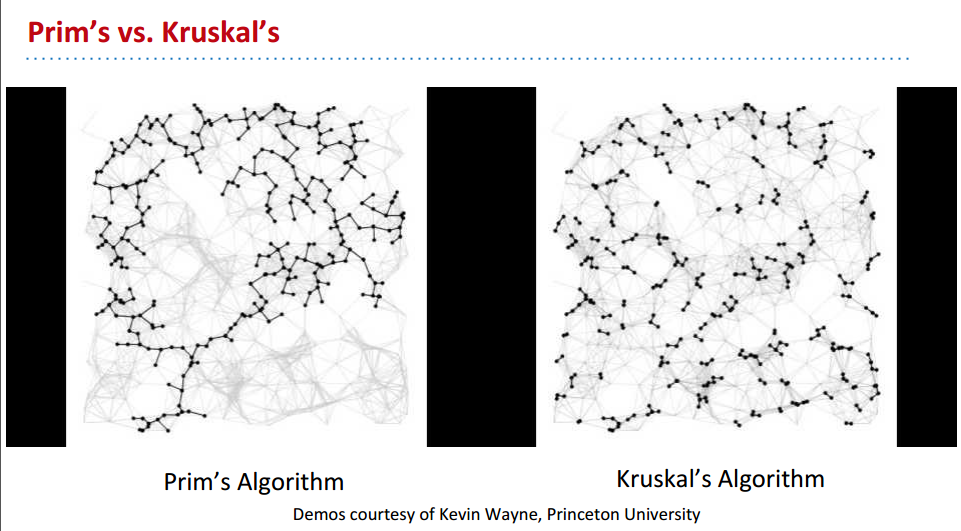
Prim's VS Kruskal's

Kruskal's pseudocode

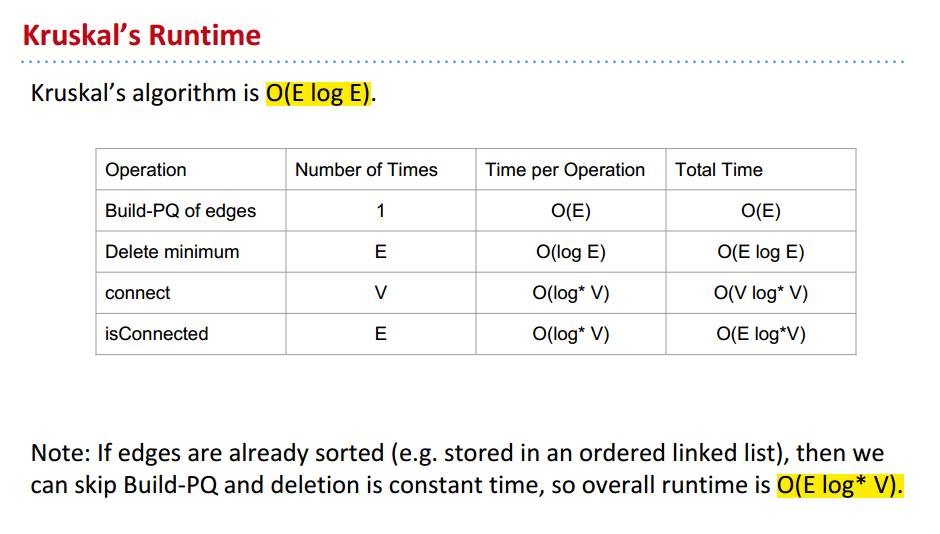
Runtime

Shortest Path and MST algorithm Summury

Minimum Spanning Trees, Kruskal's, Prim's

Overview

C LEVEL

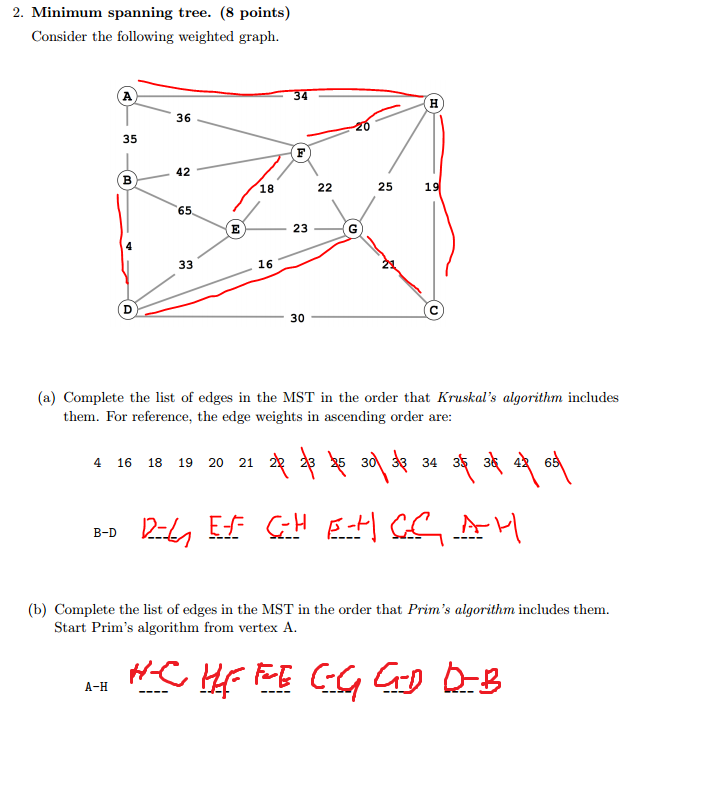
2.Problem 2 from Princeton's Spring 2008 final

Normally in alphabetic oder.

3.Would Kruskal or Prim's algorithm work on a directed graph?
No.

4.True or false: Adding a constant to every edge weight does not change the solution to the MST problem.
TRUE

B level

1.Adapted from Algorithms 4.3.8. Prove the following, known as the cycle property: Given any cycle in an edgew eighted graph (all edge weights distinct), the edge of maximum weight in the cycle does not belong to the MST of the graph.

这题用反证法，首先MST的定义要清楚：

假设the edge of maximum weight in the cycle在MST T1里，为edge e. 我们删掉C，那T1就会分成两部分，e的两个端点分别在两不同部分。cycle里其他的edge重新连接这两部分，比如edge f重新连接，形成新的MST T2. 这样的话，T1的总weights大于T2了，与T1是graph的MST矛盾。所以原假设不成立，圆里maximum weight的edge不可能属于图的MST.

Minimum spanning tree

2.Problem 3 from Princeton's Fall 2009 final (part d is pretty hard).

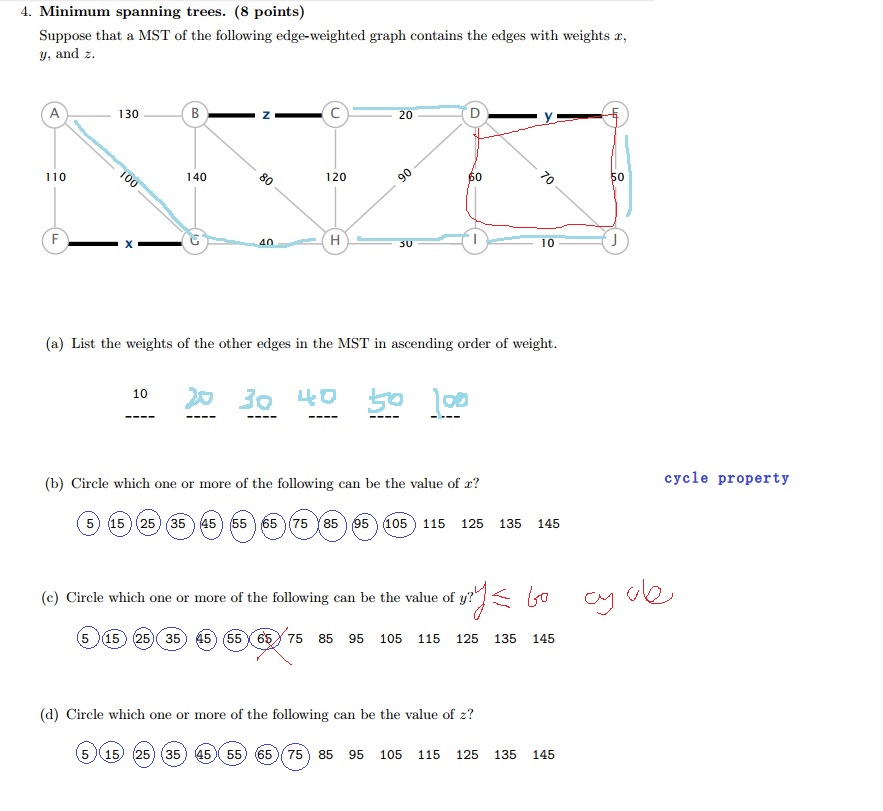
3.Problem 4 from Princeton's Fall 2012 final.

4.Adapted from Algorithms 4.3.12. Suppose that a graph has distinct edge weights. Does its shortest edge have to belong to the MST? Can its longest edge belong to the MST? Does a min-weight edge on every cycle have to belong to the MST? Prove your answer to each question or give a counterexample.

Minimum-cost edge

Cycle property