Chapter 3 Binary Tree Divide Conquer

Jiuzhang

Outline

Time Complexity Tranning

T(n) = T(n/2) + O(n)的情况 >>>> o(nlogn)

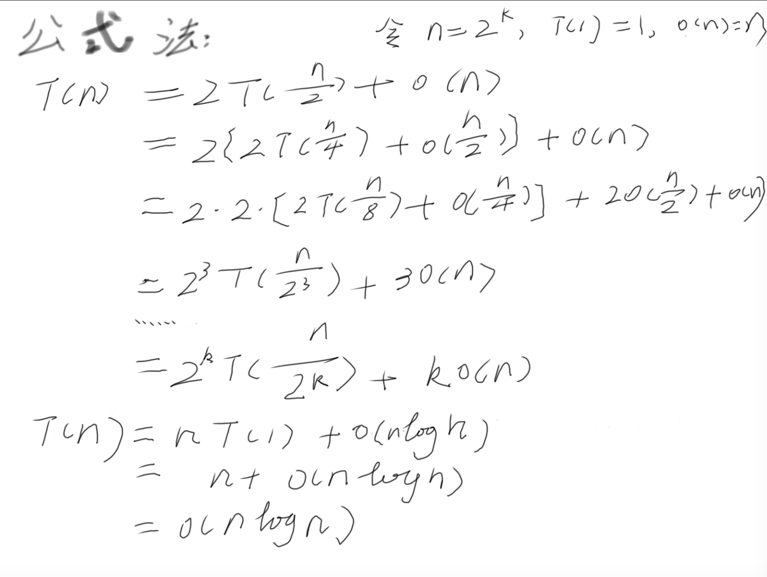
T(n) = T(n/2) + O(1)的情况 >>>> o(n)

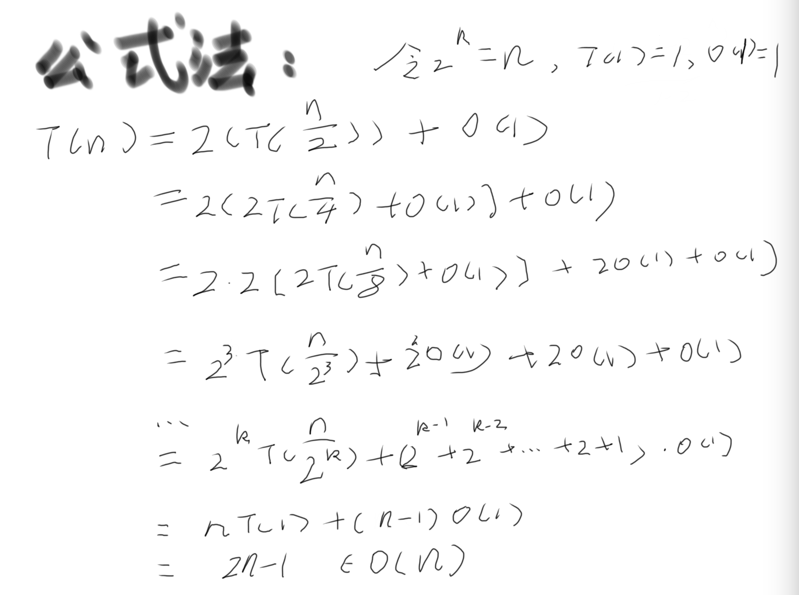
Preorder, Inorder, Postorder

会不会写这个是鉴别你会不会写程序的指标。
Non-recursion(or iterative)的preorder, inorder要求背下来, traversal和divide and conquer要求三个都会自己写。

这个视频很详细地讲解了non recursion方法的实施过程：
Preorder Traversal Without Recursion using stack

preoder traversal的non-recursive方法会用stack,老师提到，几乎所有本来用recursion很好做的题要用non recursion做的话，都会用到Stack。

注意在 while 循坏里边，是先看 temp的right child是否为空，若否则push到stack里面；再看left child。 原因是Stack是先进后出filo的数据结构。preorder是root,left,right的顺序，所以我们要在pop掉root之后，先往 stack里边push进去right,再是push进去left.

// preorder traversal non-recursive way
public class Solution {
    public ArrayList<Integer> preordertraversal(TreeNode root){
        ArrayList<Integer> preorder = new ArrayList<>();
        if (root == null) {
            return preorder;
        }
        Stack<TreeNode> stack = new Stack<TreeNode>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode temp = stack.pop();
            preorder.add(temp.val);
            if (temp.right != null) {
                stack.push(temp.right);
            }
            if (temp.left != null) {
                stack.push(temp.left);
            }
        }
        return preorder;
    }
}

preorder的traversal方法：

public class Solution{
    public ArrayList<Integer> preorderTraversal(TreeNode root){
        ArrayList<Integer> result = new ArrayList<>();
        preorder(root,result);
        return result;
    }
    private void preorder(TreeNode root, ArrayList<Integer> result){
        if (root == null){
            return;
        }
        result.add(root.val);
        preorder(root.left,result);
        preorder(root.right,result);
    }
}

preorder的divide conquer方法：

public class Solution {
    public ArrayList<Integer> preorderTraversal(TreeNode root){
        ArrayList<Integer> result = new ArrayList<>();
        if (root == null){
            return result;
        }
        //divide
        ArrayList<Integer> left = preorderTraversal(root.left);
        ArrayList<Integer> right = preorderTraversal(root.right);
        //conquer
        result.add(root.val);
        result.addAll(left);
        result.addAll(right);
        return result;
    }
}

inorder traversal non-recursive using stack:

对于具体步骤印度老师的讲解：
Inorder Tree Traversal without Recursion | GeeksforGeeks

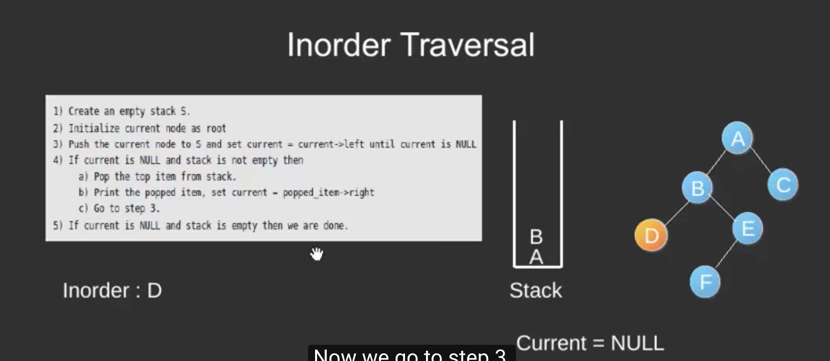
这道题我看着视频是可以理解的，但是要我自己写还是挺难写的，每一次current node的变化不好想，老师提示要背下来preorder和inorder的
non recursive方法，现在记住就好。

public class Solution {
    /**
     * @param root: The root of binary tree.
     * @return: Inorder in ArrayList which contains node values.
     */
    public ArrayList<Integer> inorderTraversal(TreeNode root) {
        // write your code here
        ArrayList<Integer> inorder = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<TreeNode>();
        TreeNode current = root;
        while (current!= null || !stack.isEmpty()){
            while (current != null){
                stack.push(current);
                current = current.left;
            }
            current = stack.pop();
            inorder.add(current.val);
            current = current.right;
        }
        return inorder;
    }
}

postorder的recursion方法

public class Solution{
    public ArrayList<Integer> postorderTraversal(TreeNode root){
        ArrayList<Integer> result = new ArrayList<>();
        if (root == null) {
            return result;
        }
        //divide
        TreeNode left = postorderTraversal(root.left);
        TreeNode right = postorderTraversal(root.right);
        //conquer
        result.addAll(left);
        result.addAll(right);
        result.add(root.val(;
        return result;
    }
}

traverse和divide conquer的主要联系和区别：
- 他们都是递归方法
- traverse的result会被当作参数传到方法体内；divide conquer的result会直接返回

Quicksort Mergesort