Search a 2D Matrix

LeetCode LintCode

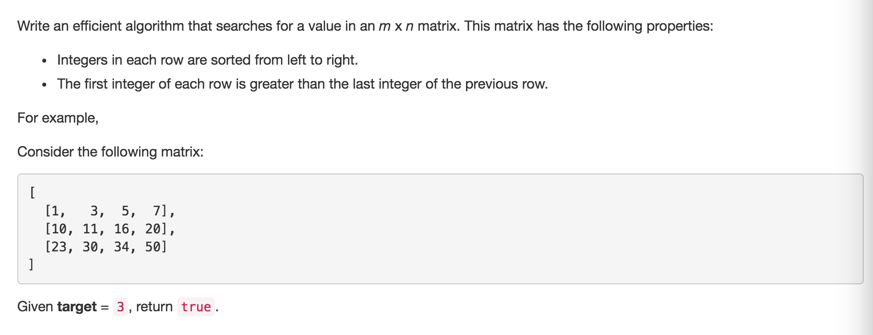
我想出来的方法比较straightforward, 就是先确定行，再确定列。两次使用binary search. 其中实施起来有不少细节容易错，值得细细推敲。值得留意的是，这道题可以看出来LeetCode的通过检测比LintCode要严格，以后都要到LeetCode上测试。

public class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if ( matrix == null || matrix.length == 0){
            return false;
        }
        if (matrix[0] == null || matrix[0].length == 0) {
            return false;
        }
        int row = matrix.length;
        int column = matrix[0].length;
        int start = 0;
        int end = matrix.length - 1;
        while (start + 1 < end){
            int mid = start + (end - start) / 2;
            if ( target == matrix[mid][0]){
                return true;
            } else if (target > matrix[mid][0]){
                start = mid ;
            } else {
                end = mid;
            }
        }
        if (target >= matrix[end][0]){
            row = end;
        } else if (target >= matrix[start][0]) {
            row = start;
        } else{
            return false;
        }
        start = 0;
        end = column - 1;
        while (start + 1 < end){
            int mid = start + ( end - start ) / 2;
            if ( target == matrix[row][mid]){
                return true;
            } else if (target < matrix[row][mid]) {
                end = mid;
            } else{
                start = mid;
            }
        }
        if (matrix[row][start] == target) {
            return true;
        }
        if (matrix[row][end] == target){
            return true;
        }
        return false;
    }
}

这个首先要套用老师讲的二分法的模版：

首先要注意几种特殊情况，这里特别提一下以下情况：

        if (matrix[0] == null || matrix[0].length == 0) {
            return false;
        }

matrix[0] == null

表示的是有一个[ ]，但它里面的2D array还没有初始化；而

matrix[0].length == 0

则是代表 [ [ ] ] 这样子的情况。

我们第一步先确定target所在的行，以mid行的第一列为标准作为判断来变化start, end. 退出循环后，只剩下start, endl两行，再检查target与这两行第一列的关系。首先检查第二行第一列跟target的关系，最终确定行数。

第二步，继续二分法确定列数。循环条件按照模版很类似，循环内容也是模版的A[mid] ==, <, > target 这几种情况。循环结束只需要再多检查该行的start, end两列是否为target。

几乎都是按照这个模版：

start + 1 < end
start + (end - start) / 2
A[mid] ==, <, >
A[start] A[end] ? target

第二种方法是用一次二分法。

public class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if ( matrix == null || matrix.length == 0){
            return false;
        }
        if (matrix[0] == null || matrix[0].length == 0) {
            return false;
        }
        int row = matrix.length;
        int column = matrix[0].length;
        int start = 0;
        int end = row * column - 1;
        while (start + 1 < end) {
            int mid = start + (end - start) / 2;
            if (target == matrix[mid / column][mid % column]){
                return true;
            } else if (target < matrix[mid / column][mid % column]){
                end = mid;
            } else {
              start = mid;  
            }
        }
        if (target == matrix[start / column][start % column]){
            return true;
        }
        if (target == matrix[end / column][end % column]){
            return true;
        }
        return false;
    }
}

感觉这个方法胜在抽象思维，将2d array整体抽象成 col * row 个元素。这里的end定义为最后一个元素的index, 所找到的mid是所有元素最中间的那个，而跟行列无关。 循环结束后，我们的start, end直接是相邻的两个元素的index, 所以再检查这两个元素即可。