Lecture 22: Balanced Search Trees

CS61B

2-3-4 and 2-3 Trees (a.k.a. B-Trees)

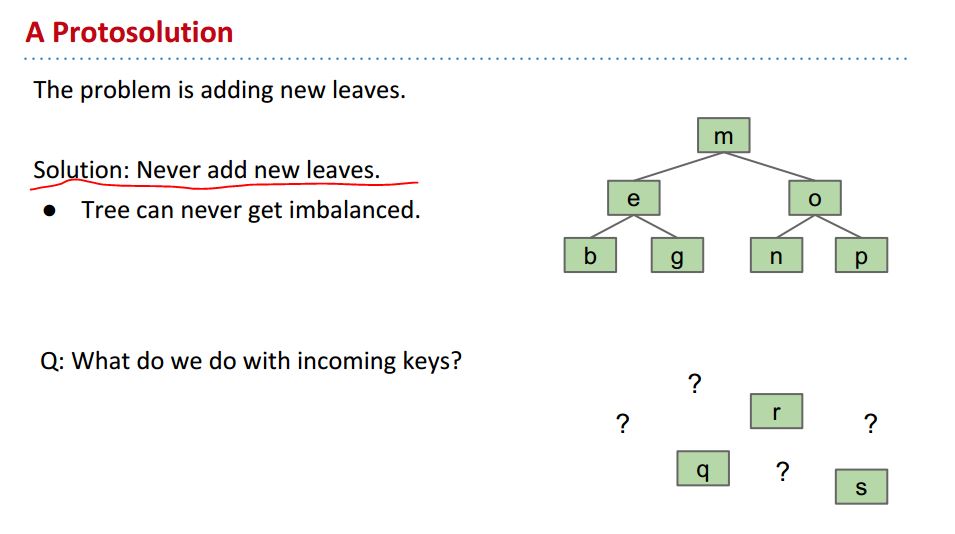
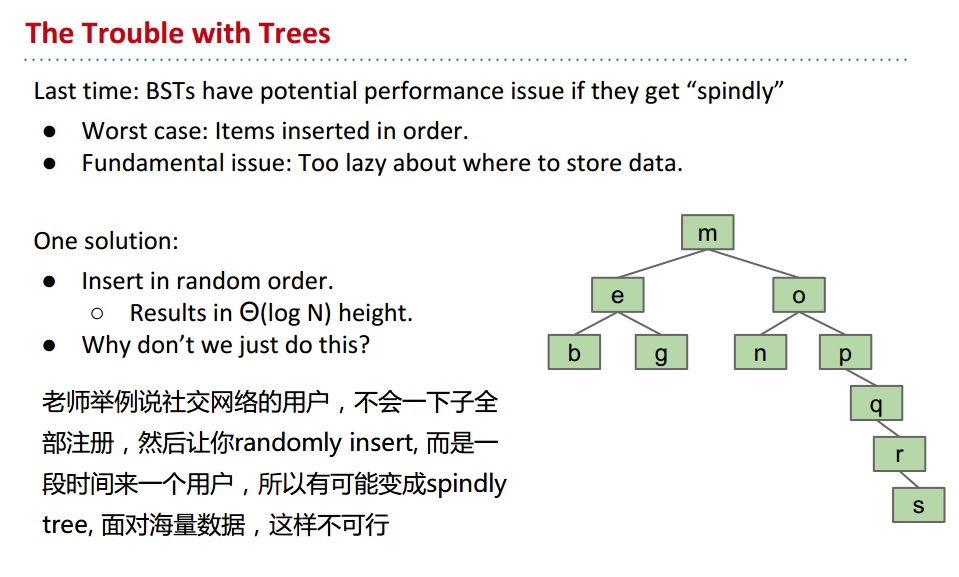
先是指出现有树的不足：

为了解决这个问题，solution是永远不要增加新的树叶：

但也带来了新的问题，怎么添加新元素呢？

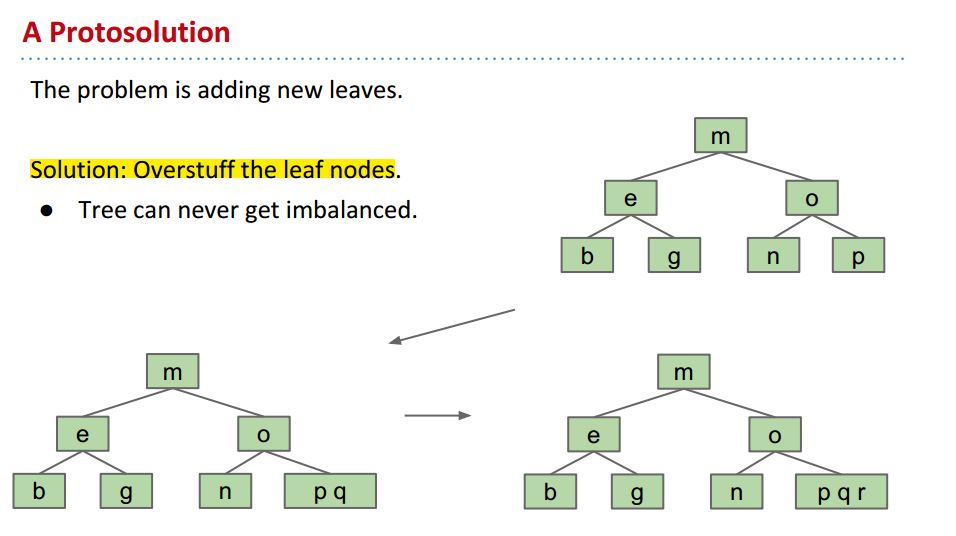
这个问题的solution是硬塞：

但这样又带来新的问题，树叶变得too juicy， 也就是每个Node里有太多元素，满得要溢出来，并且有的结点意义不明：

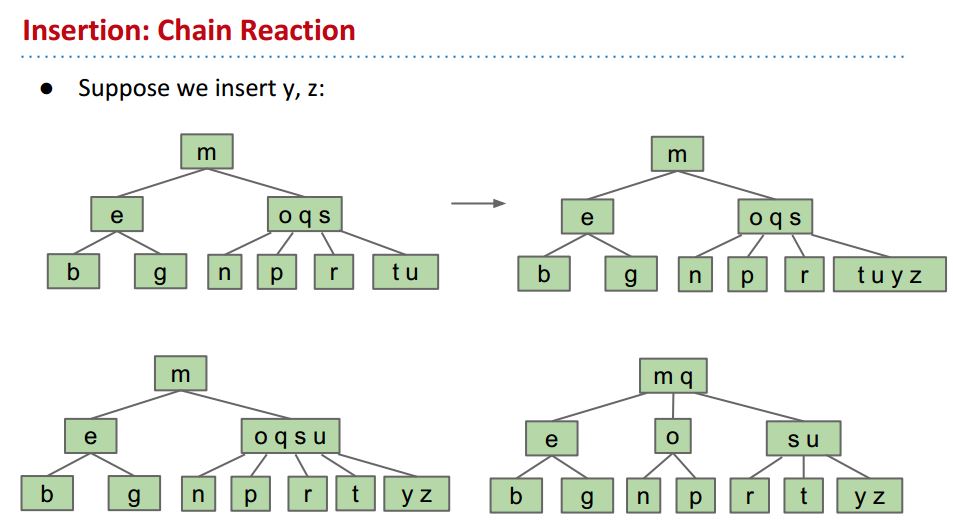
这个问题的solution是，为每个结点所能容纳的元素数设置上限，比如3；多出来的就移给它的父树枝，然后把子树枝里面含有较多元素的split开来：

下面是例子，可以做看看自己是否理解insert该怎么split：

下面又有一个问题，如果根树枝的元素数量达到上限了，该怎么办？

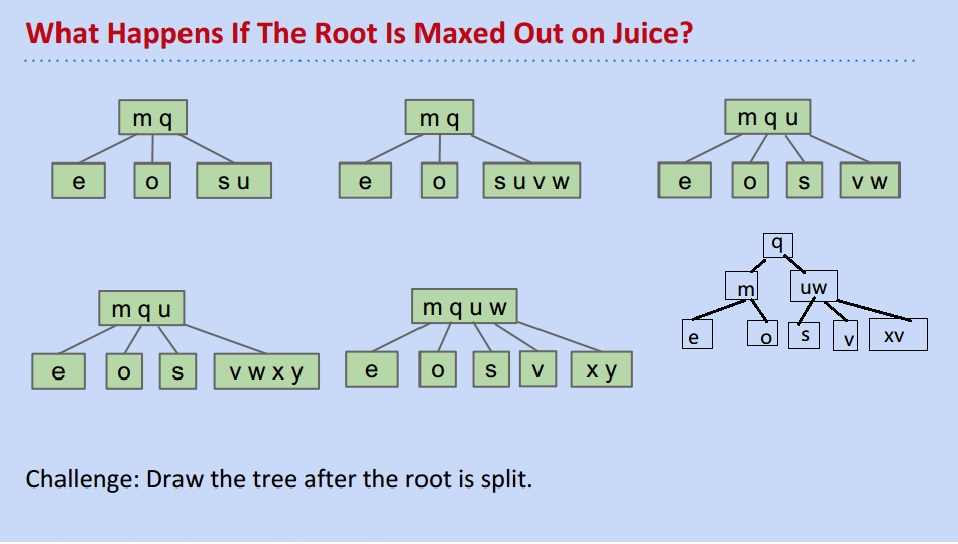
答案没问题：

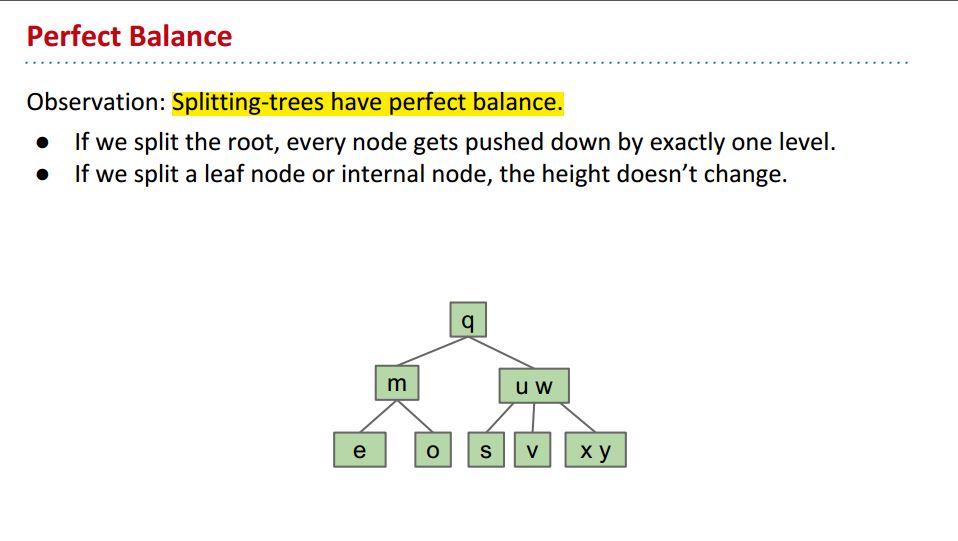
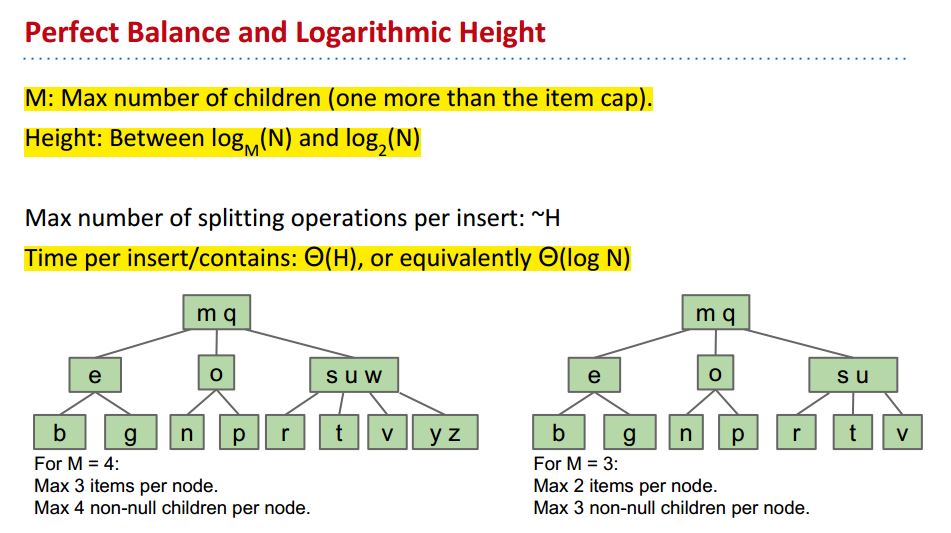
这里有一个结论：splitting trees have perfect balance.
就是通过这种分割方式得到的树都是perfect balanced

Perfect Balanced tree的定义是从任何一个分支端点走到根结点，都是一样的长度：

按照定义，这也是perfectly balanced tree:

Spiltting tree的高度介于Logm（N） 跟log₂（N）之间，
每个Node至少2个children,最多Height = log₂（N）很好理解，

splitting tree很形象，但是它们的名字是叫B-trees, a B-tree of order M = 4也叫做2-3-4 tree或者2-4tree,这个名字代表每一个Node能有的元素上线数：

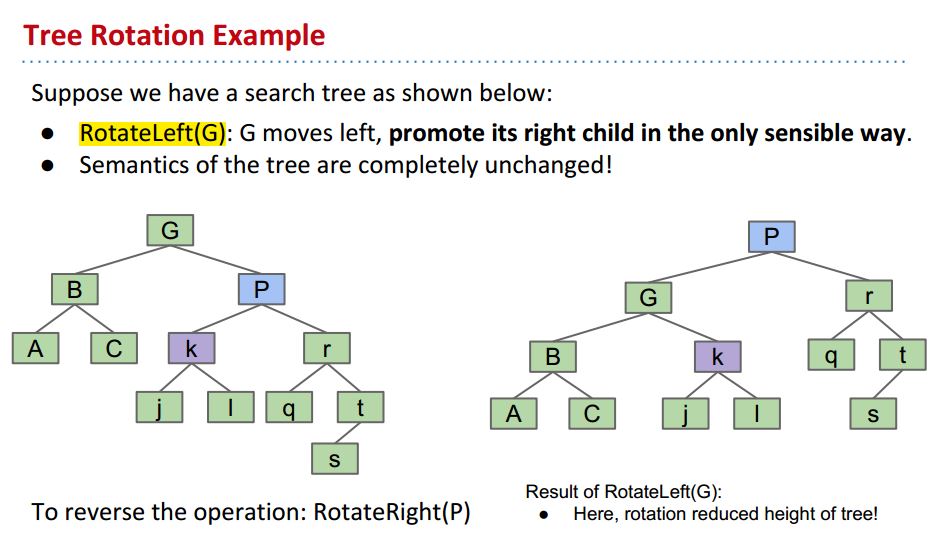
Tree Rotation

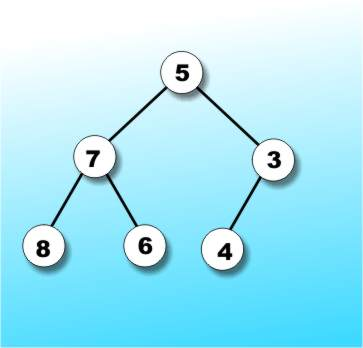
先看下rotate的例子：

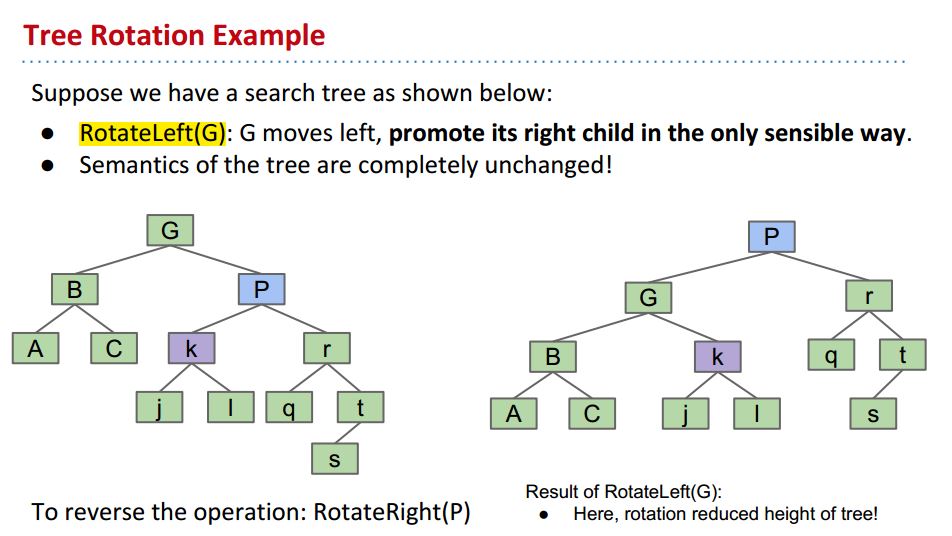
自己试着rotate一个：

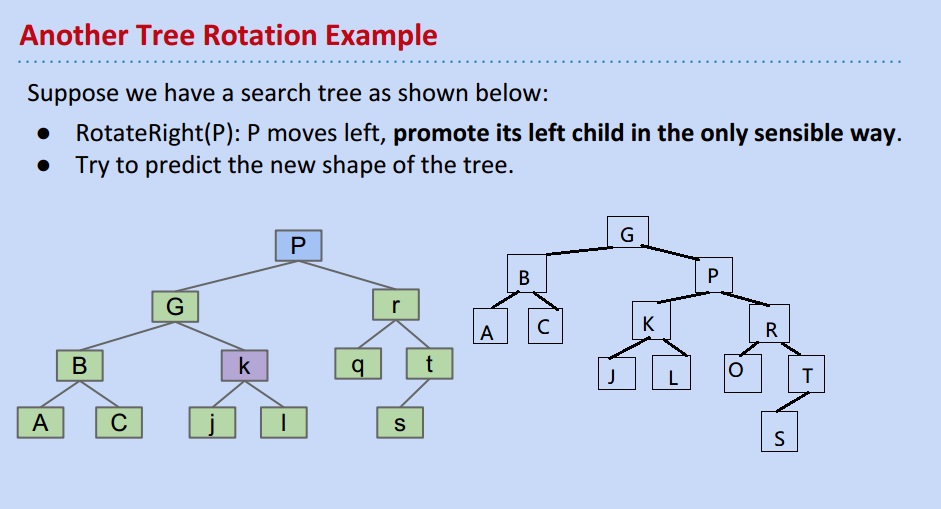
答案没毛病：

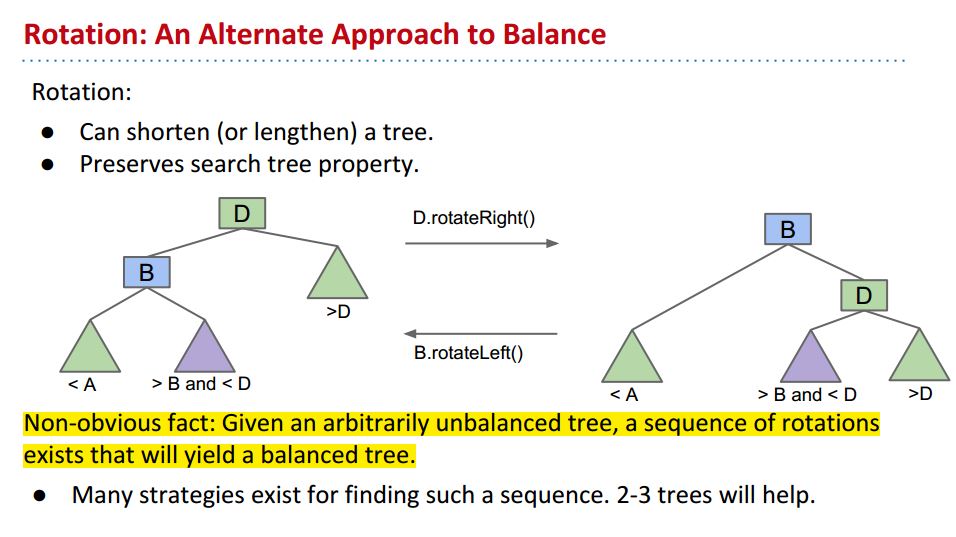
下面有一个结论，现在还没有给出证明：任何一个不平衡的数，通过一系列的rotate,都可以得到一个平衡的树

Red-Black Trees

我们想用一个Binary Tree来代表一个2-3 Tree,因为2-3 Tree有一些令人恼火的特性：代码很tricky, 每个Node的children数量是变量……

于是，我们用一个glue-link来代表一个3结点：

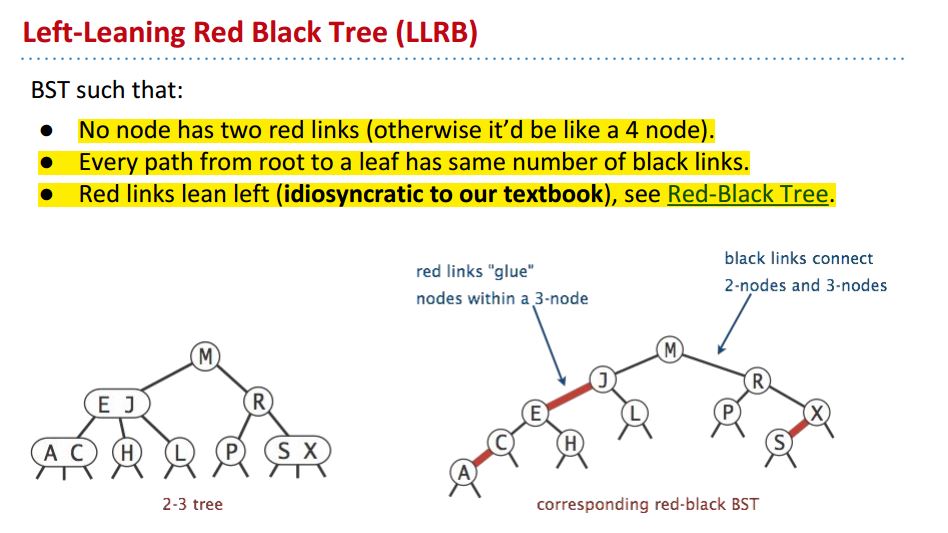
Left-leaning Red Black Tree(LLRB)的定义：

• 没有结点有两条红色的连结线
• 从根节点到叶结点的路径都有相同的黑色连结线数量
• 红色的连结线向左倾斜

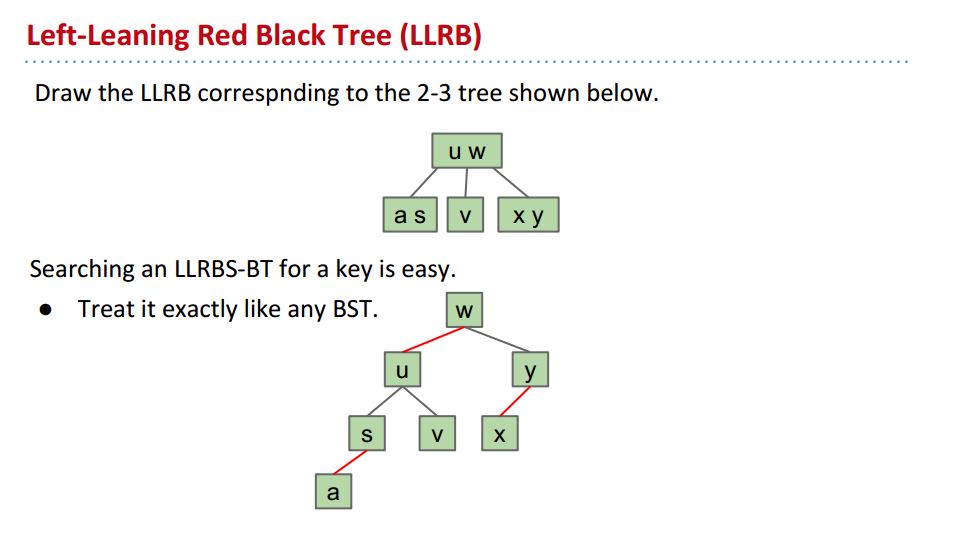
试着自己画一个LLRB：

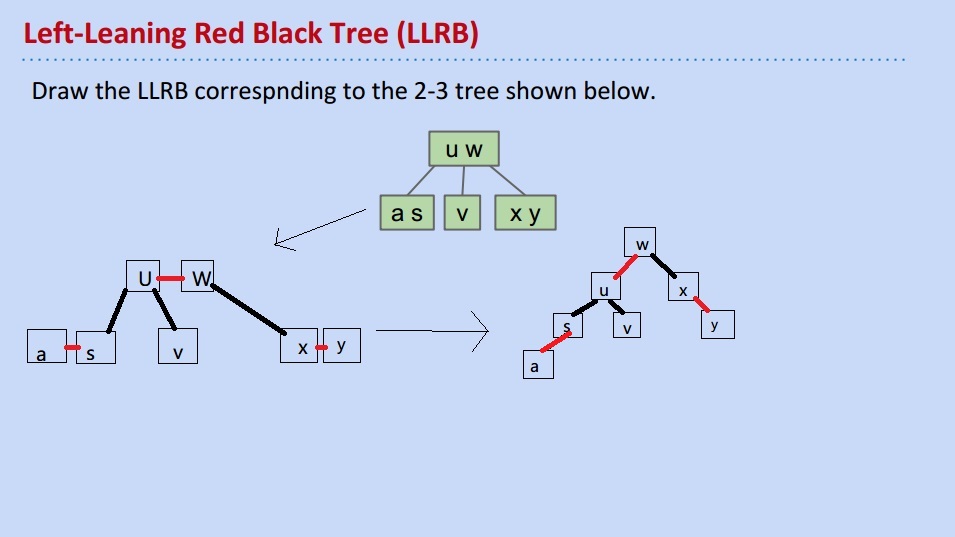
跟答案稍有出入，

at first I thought they are both correct,仔细一看，我的LLRB没有满足LLRB的第三个条件：Red links lean left,所以还是不正确，修改：

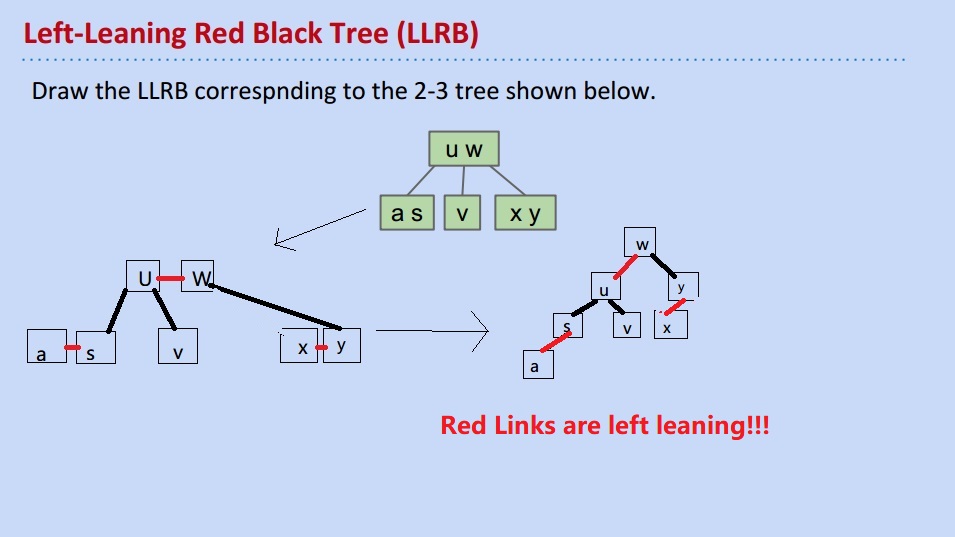
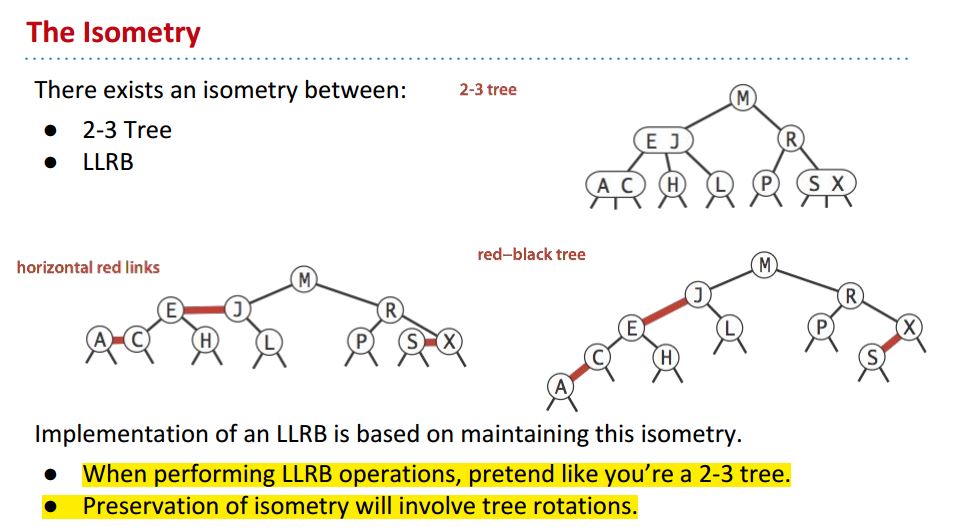
slides说2-3 tree和LLRB之间有Isometry, 这个单词是等距的意思，我理解为2-3 Tree和LLRB tree可以相互转换：

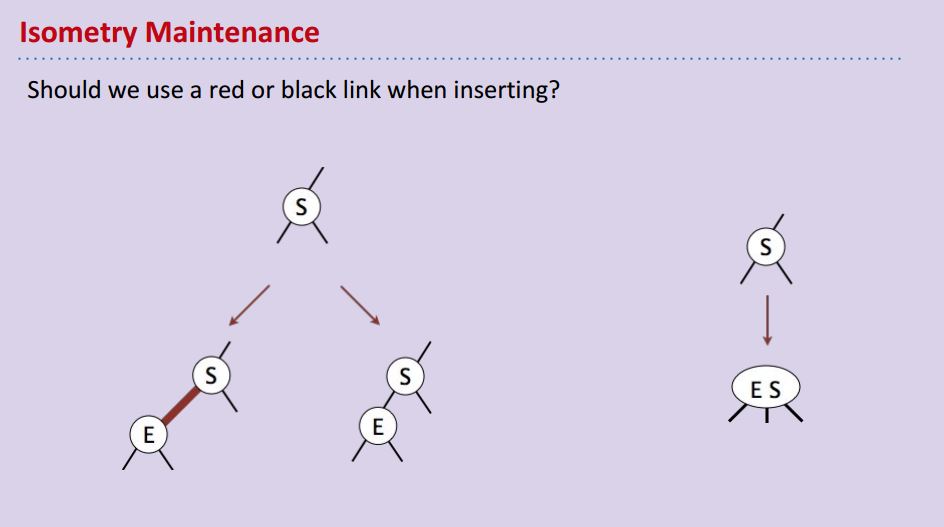
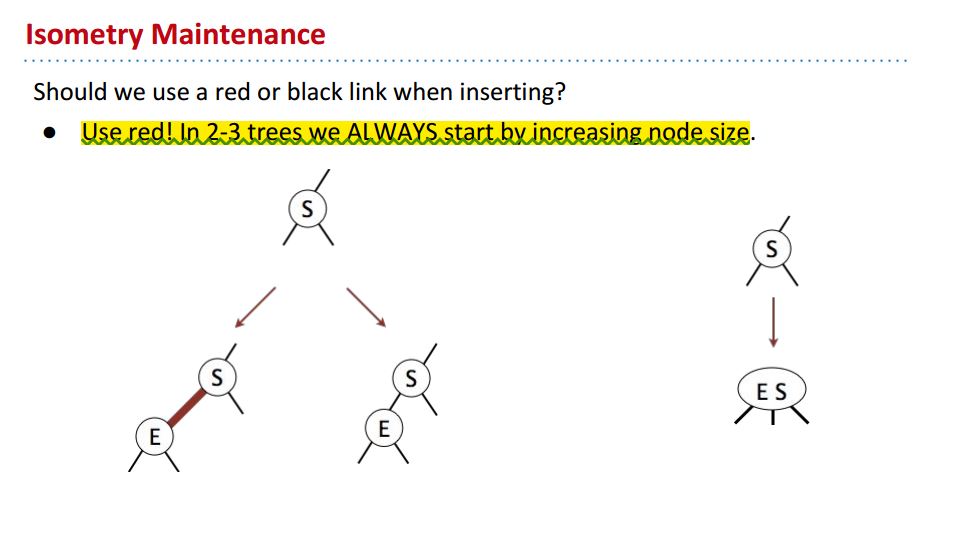
那么为了保持这种2-3 tree跟LLRB tree之间的对应关系，类比于2-3 tree, 在LLRB tree中Insert新元素的时候，是应该用red link 还是black link呢？

答案很简单，在2-3 tree里我们insert时，首先肯定是塞满一个node, 也就是让新元素glue link to 那里本来就有的元素（黏在一起），在红黑树里就要用red link：

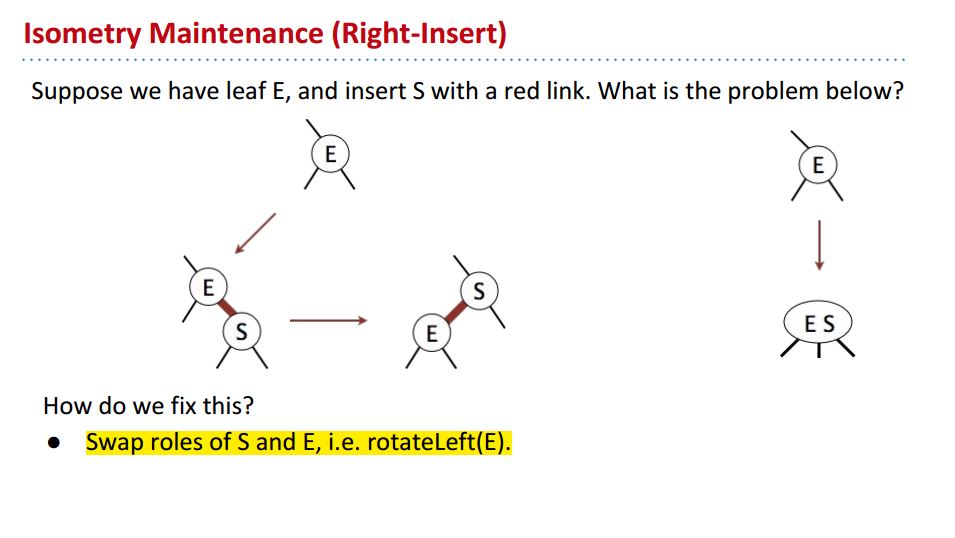
转换成红黑树的时候还会遇到一个问题，也是我自己刚刚遇到的，就是我们的red link有可能是右倾而不是左倾的：

solution很简单，rotate即可。

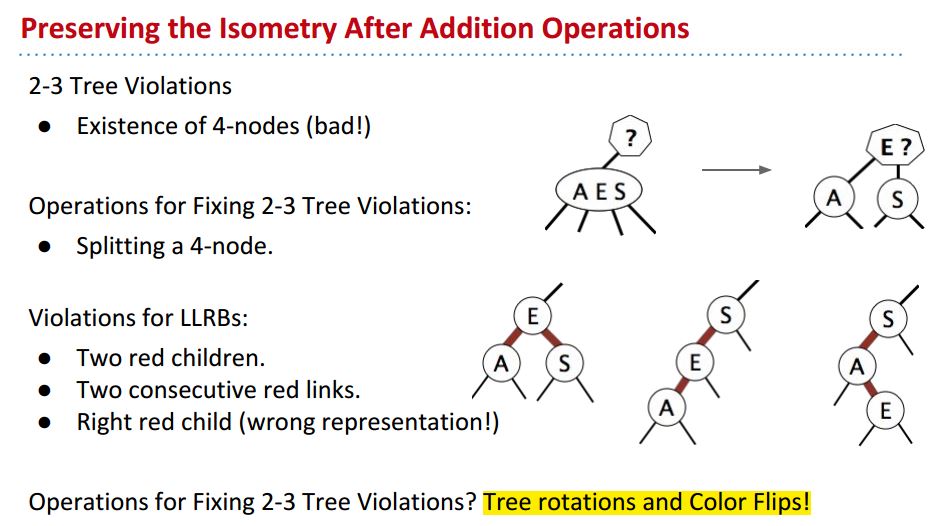
保持isometry的三种重要情况：

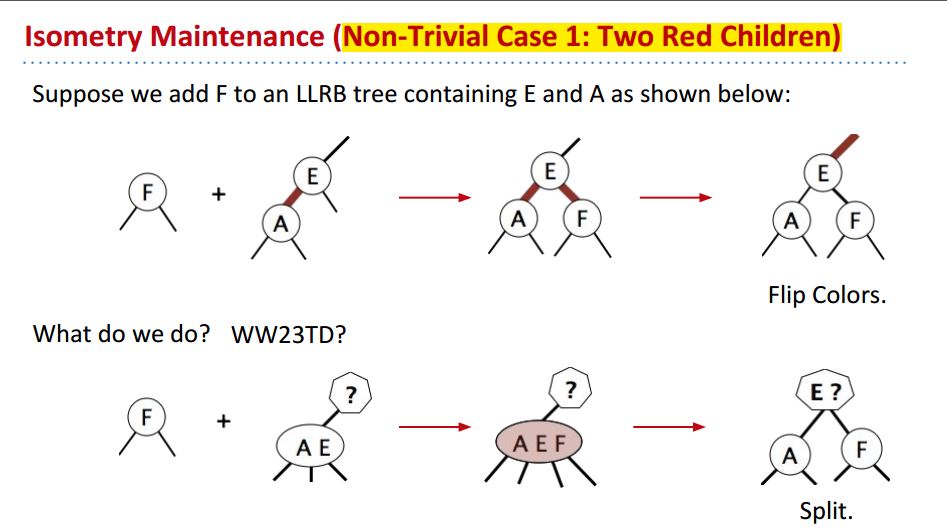
第一种情况：two red children:
在2-3 tree里我们会遇到一种情况，向一个Node中Insert元素的时候，达到元素数量的cap，这时候我们会split the node,然后 send up其中一个元素to parent node,红黑树中也有相对应的情况，就是一个Node周围有两条red links,这时候怎么办呢？

solution是Flip colors, 这里有一些magic, 但只要调换颜色就可以。

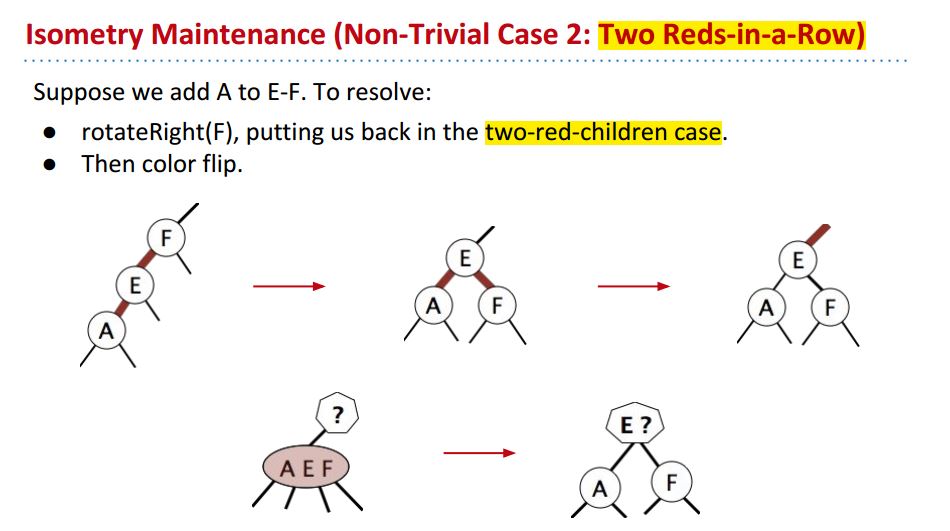
第二种情况：two reds-in-a-row
这种情况先rotate一下变成two red children的第一种case，接下来相同方法处理：

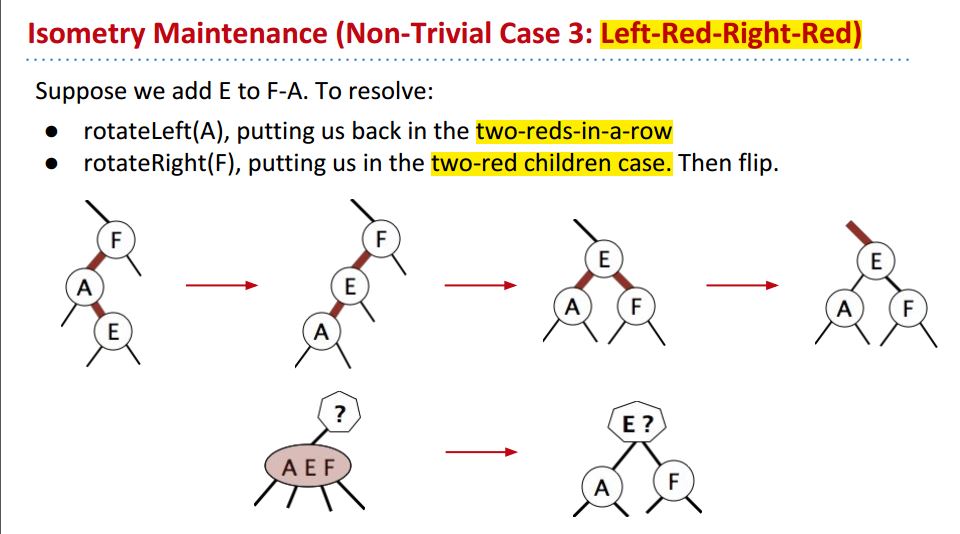
第三种情况是red left red right:
这种情况的solution是先rotate成case two: two reds-in-a-row;再rotate成case one: two red children来处理：

一言以蔽之，类比于2-3 tree, 我们的LLRB tree 保持isometry的方法就是Tree rotations and Color Flips!

Summary: