五、动态最优（III）动态规划方法

樊潇彦 复旦大学经济学院 数量经济学

0. 准备工作

setwd("D:\\...")   # 设定工作目录
rm(list=ls())      # 清内存
# "Ctrl"+"L" 清除命令窗口
install.packages("parallel")

1. 模型设置

discount <- 0.95                                       # 贴现因子 beta^t
gamma <- 1                                            
if (gamma==1){u.fmla <- expression(log(c))
}else{
  u.fmla <- expression(c^(1-gamma)/(1-gamma))}         # 效用函数表达式
u <- deriv(u.fmla, "c", function(c) {})                # u(c)
alpha <- 0.5    
f.fmla <- expression(z*k^alpha)                        # 生产函数表达式
f <- deriv(f.fmla, c("k","z"), function(k,z) {})       # y=f(k,z)
delta <- 1                                             # 折旧率
kprime.fmla =expression(z*k^alpha + k*(1-delta) - c)   # k_t+1表达式
kprime <- deriv(kprime.fmla, c("k","z","c"),           # k_t+1(k,z,c)
                function(k,z,c) {})
z=zss=1
kss <- ((1/discount+delta-1)/alpha)^(1/(alpha-1))      # 稳态
css <- f(kss,zss) - delta*kss  
NK=100
k.grid <- seq(0.01,3*kss,length.out=NK)                # 设置k的格点                  

2. 价值函数迭代

library(parallel)
v.change <- 100; tol <- 1e-4                                 # 迭代设置
iterations <- 0; maxiter=100
c_min=kprime_min=0.01
# 在每个格点上给出初始猜测,v0(k_i)，比较好的初始猜测将大大提高迭代效率
#v.grid <- rep(0,NK) 
v.grid <- rep(u(css)/(1-discount),NK)    
v0 <- approxfun(k.grid, v.grid, rule=2, method="linear")     # 在格点之间用内插方法得到连续的v0(k) 
v.app <- list()                                              # 用list存放v的迭代数据
v.app[[1]] <- v0
while(v.change > tol || iterations<maxiter) {
  bellman <- mcmapply(function(k) {                          # v(k_i)
    c_max=f(k,zss) + (1-delta)*k - 0.01
    optimize(function(c) {                                   # = max_c (u + beta*v(kprime))
      u(c) + discount*v0(kprime(k,zss,c)) },
      interval=c(c_min, c_max),                              
      maximum=TRUE
    )
  }, k.grid)
  v.g.new <- unlist(bellman["objective",])                   # v1(k_i)  
  v.change <- max(abs(v.g.new-v.grid))                       # 判断是否收敛
  iterations <- iterations+1
  v.grid <- v.g.new                                          # 更新v0(k_i)=v1(k_i)
  v0 <- approxfun(k.grid,v.grid,rule=2,method="linear")      # 拟合v0(k)
  v.app[[iterations+1]] <- v0                                # 存放
  print(sprintf("After %d iterations v.change=%.2g\n",iterations,v.change))
}
c.grid=unlist(bellman["maximum",])                           # 最优策略c(k_i)
data<- data.frame(k=k.grid, c=c.grid,  k.new=kprime(k.grid,zss,c.grid), f=f(k.grid,zss),
                  v1=v.app[[1]](k.grid), v2=v.app[[2]](k.grid),
                  v11=v.app[[11]](k.grid), v51=v.app[[51]](k.grid), 
                  v=v0(k.grid))

3. 作图

library(ggplot2)
value=ggplot(data,aes(x=k)) +                                # 价值函数
  geom_line(aes(y=v1,colour="V(0)：Initial guess")) +
  geom_line(aes(y=v2,colour="V(1)"))+
  geom_line(aes(y=v11,colour="V(10)")) +
  geom_line(aes(y=v51,colour="V(50)")) +  
  geom_line(aes(y=v,colour="V_converged")) +
  theme_minimal() +
  scale_colour_discrete(name="") +
  scale_y_continuous("v(k)") +
  scale_x_continuous("k") 
if (gamma==1 & delta==1){                                    # 特殊设定，用理论值检验V(k) 
  theta0=1/(1-discount)*(alpha*discount*log(alpha*discount)/(1-alpha*discount)+log(1-alpha*discount))
  theta1=alpha/(1-alpha*discount)
  vcheck.grid=theta0+theta1*log(k.grid)
  data=data.frame(data,vcheck=vcheck.grid)
  head(data.frame(v.grid, vcheck.grid))
  tail(data.frame(v.grid, vcheck.grid))
  value <- value + geom_line(aes(y=data$vcheck,colour="V_theory")) 
}
value

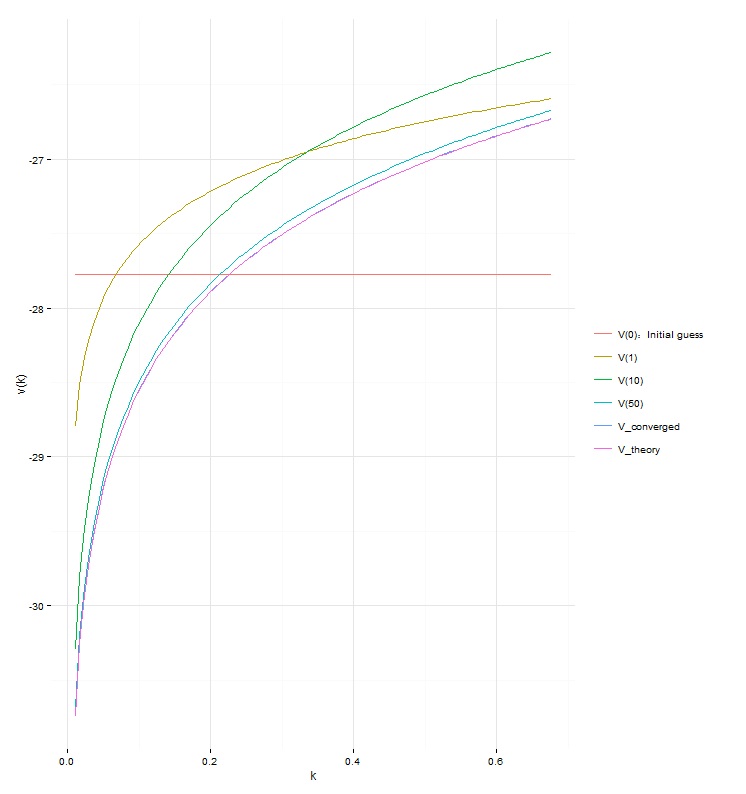
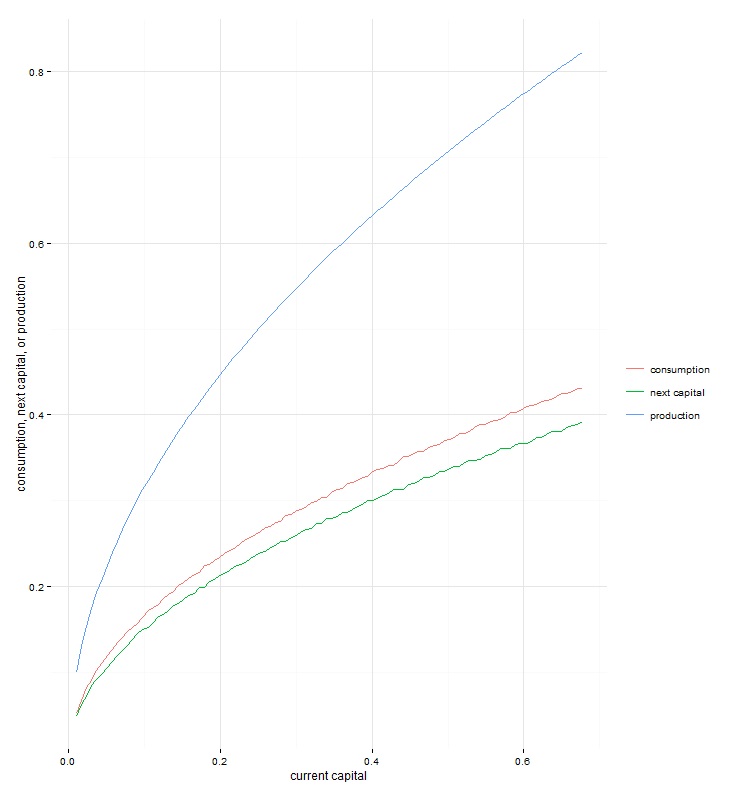
4. 策略函数

policy <- ggplot(data,aes(x=k))+                             # 策略函数
  geom_line(aes(y=c,colour="consumption"))  +
  geom_line(aes(y=k.new,colour="next capital")) +
  geom_line(aes(y=f,colour="production")) + 
  theme_minimal() +
  scale_colour_discrete(name="") +
  scale_y_continuous("consumption, next capital, or production") +
  scale_x_continuous("current capital")
policy

在线课程资料

1. Thomas J. Sargent and John Stachurski: Quantitative Economics
2. Paul Schrimpf: Mathematics for economics