第十三讲 极值理论、分位数估计与VaR

樊潇彦 复旦大学经济学院 金融数据

---

Ch13_data_code.rar54.9kB

setwd("D:\\..\\Ch13")
install.packages("sm","quantreg","evir")
## 调用
library(sm)
library(quantreg)
library(evir)
library(stats)
library(fPortfolio)
library(RQuantLib)
library(qcc)
library(rugarch)
library(fGarch)
library(zoo)
library(tseries)
library(forecast)
library(timeSeries)
library(tidyverse)
library(readxl)
library(ggplot2)

1. 风险测度

根据巴塞尔协议，金融风险被分为三类：市场风险、信用风险和操作风险。一个与基本金融理论一致的市场风险测度 $\eta$ 应满足下面四个条件（$X,Y$ 为随机变量，$c\ge 0$）：

1. 次可加性： $\eta(X+Y)\le\eta(X)+\eta(Y)$

2. 单调性： $X\le Y \Rightarrow \eta(X)\le \eta(Y)$

3. 正齐性： $\eta(cX)=c\eta(X)$

4. 变换不变性：$\eta(X+c)=\eta(X)+c$

1.1 风险值（Value at Risk, VaR）

一个金融头寸在时刻 $t$ 的价值记为 $V_t$，在接下来的 $l$ 期的损失

$$L_t(l) = V_{t+l} -V_t$$
假定随机变量 $L_t(l)$ 的累积分布函数为 $F_l$，我们把 $VaR_{1-p}$ 定义为一个可能面临的巨大损失：
$$VaR_{1-p} = \text{inf} \left\{x|F_l(x)\ge 1-p\right\}\Leftrightarrow\int_{ - \infty }^{VaR} {f\left( x \right)dx} = 1 - p$$
对于一元函数，VaR 就是损失分布的 $q=1-p$ 分位数。相应地有：
$$Pr[L_t(l)>VaR_{1-p}] \le p \Leftrightarrow \int_{VaR}^\infty {f\left( x \right)} dx = p$$

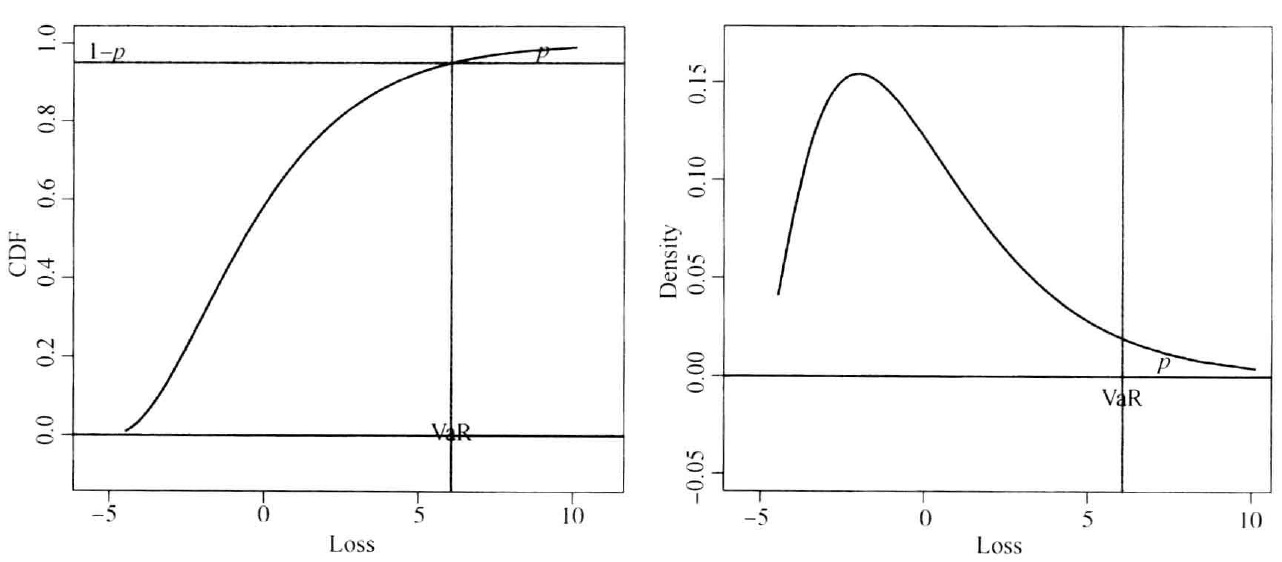
• 对于正态分布、学生分布等常用分布，VaR的计算非常方便。
  
  • 损失变量服从正态分布 $X \sim N\left( {{\mu _t},\sigma _t^2} \right)$：
    $$Va{R_{1 - p}} = {\mu _t} + {z_{1 - p}}{\sigma _t}$$
  • 标准化损失变量 $Y$ 服从自由度为 $\nu$ 的学生分布 $Y=\frac{{X - {\mu _t}}}{{{\sigma _t}}} \sim {t_v}$：
    $$Va{R_{1 - p}} = {\mu _t} + {t_{1 - p,\nu}}{\sigma _t}$$

mn=0.01; sd=2; p=0.05; q=1-p; nu=5            # 参数设定 
set.seed(1)
rn=rnorm(1000)                                # 模拟数据             
rt=rt(1000,nu)                                # 可以用 plot(density(rn)) 命令画密度线
y = c(rn,rt)
g = factor(rep(c("r_n","r_t"), each=1000))    # 用因子变量标记两组
library(sm)
sm.density.compare(y, g)                      # 合并做图，进行比较
legend("topright", levels(g), fill=2+(0:nlevels(g)))
title(main="正态分布和学生分布密度曲线")
z=qnorm(q); t=qt(q,nu)
VaR_n=mn+z*sd                                 # （7-2）正态分布VaR
VaR_t=mn+t*sd                                 # （7-3）学生分布VaR
data.frame(VaR_n, VaR_t)

• 当损失服从正态分布时，VaR是一致风险度量；但一般而言，VaR并不满足一致性条件。
• VaR 只是右尾概率的p分位数，并没有描述实际尾部行为。

1.2 期望损失（Expected Shortfall, ES）

定义 ES 为损失 $X>VaR$ 时的期望值，也称为条件或尾部风险值（CVaR，TVaR）。

$$E{S_{1 - p}} = E\left( {X|X > VaR} \right) = \frac{{\int_{VaR}^\infty {xf\left( x \right)dx} }}{{\Pr \left( {X > VaR} \right)}} = \frac{{\int_{1 - p}^1 {Va{R_u}du} }}{p}$$

• 损失变量服从正态分布 $X \sim N\left( {{\mu _t},\sigma _t^2} \right)$：
  $$E{S_{1 - p}} = {\mu _t} + \frac{{f\left( {{z_{1 - p}}} \right)}}{p}{\sigma _t}$$
• 标准化损失变量 $Y$ 服从自由度为 $\nu$ 的学生分布 $Y=\frac{{X - {\mu _t}}}{{{\sigma _t}}} \sim {t_v}$：
  $$E{S_{1 - p}} = {\mu _t} + \frac{{{f_v}\left( {{t_{1 - p,v}}} \right)}}{p}{\sigma _t}\left( {\frac{{\nu + t_{1 - p,\nu }^2}}{{\nu - 1}}} \right)$$

fz=dnorm(z); ft=dt(t,nu)
ES_n=mn+fz/p*sd                               # （7-6）正态分布ES
ES_t=mn+ft/p*sd*(nu+t^2)/(nu-1)               # （7-7）学生分布ES
data.frame(ES_n,ES_t)

1.3 风险度量制（$\text{RiskMetrics}^{\text{TM}}$）方法

定义第 $t$ 期的损失率：

$${x_t} = \left\{ {\begin{array}{*{20}{c}} {{r_t},~~~~\text{空头}}\\ { - {r_t},~~\text{多头}} \end{array}} \right.$$
第 $t$ 期建仓并持有 $l$ 期的损失率和相应的风险值为：
$$\begin{array}{l} {x_t}(l) = {x_t} + {x_{t + 1}} + ...{x_{t + l}}\\ Va{R_t}(l) = {V_t} \times {x_t}(l) \end{array}$$
如果 $x_t$ 服从无漂移的 IGARCH(1,1) 过程：
$$x_t=\sigma_tz_t\\ \sigma^2_t = \alpha \sigma^2_{t-1} + (1-\alpha)x^2_{t-1},~~0<\alpha<1$$
则基于信息 $F_t$ 的条件期望：
$$E(\sigma^2_{t+l}|F_t)=E(\sigma^2_{t+l-1}|F_t)=...E(\sigma^2_{t+1}|F_t)$$
从而有：
$$Var(x_{t+l}|F_t)=l\times \sigma^2_{t+1}$$
因此损失率服从正态分布 $x_t\text{~}N(0,l\sigma^2_{t+1})$，相应有 VaR 计算的时间平方根准则（squqre root of time rule）：
$$VaR_t(l)=\sqrt{l} \times VaR_{1-p}$$
需要注意的是，当损失率不满足均值为零、方差均值为零的特殊IGARCH(1,1)的假设，上述准则就失效了。

# P266：IBM股票
da=read.table("d-ibm-0110.txt",header=T)
head(da)
ibm=log(da[,2]+1)
source("RMfit.R")
mm=RMfit(ibm)
# 用rugarch包复制结果
library(rugarch)
igarch=ugarchspec(variance.model = list(model="iGARCH"), 
        mean.model = list(armaOrder=c(0,0),include.mean=F),    # 均值方程截距为0
        fixed.pars=list(omega=0))                              # 方差方程截距为0
igarch.fit=ugarchfit(spec=igarch, data=ibm)
igarch.fcst = ugarchforecast(igarch.fit, n.ahead=1)
ibm_sd=as.numeric(igarch.fcst@forecast$sigmaFor)               # 预测sigma_T(1)
names(igarch.fit@fit)
c(alpha=1-as.numeric(igarch.fit@fit$coef[2]),
  sd=as.numeric(igarch.fit@fit$se.coef), 
  ibm_sd=ibm_sd)                                               # 回归结果
ibm_mn=0; p=c(0.05,0.01,0.001); q=1-p
z=qnorm(q)
ibm_VaR_n=ibm_mn+z*ibm_sd                                      # VaR
fz=dnorm(z)
ibm_ES_n=ibm_mn+fz/p*ibm_sd                                    # ES
data.frame(p, ibm_VaR_n, ibm_ES_n)            
# P267：汇率
da1=read.table("d-useu0111.txt",header=T)
head(da1)
rt=diff(log(da1[,4]))
m2=RMfit(rt)

2. VaR计算的计量经济学方法

2.1 基于ARIMA-GARCH模型参数估计

为损失率 $x_t$ 建立ARIMA(p,q)-GARCH(m,n)模型：

$$\begin{array}{l} x_t=\phi_0+\sum_{i=1}^{p}{\phi_ix_{t-i}}+\varepsilon_t-\sum_{j=1}^{q}{\theta_j\varepsilon_{t-j}}\\ \varepsilon_t=\sigma_tz_t\\ \sigma^2_t=\alpha_0+\sum_{i=1}^{m}{\alpha_i\varepsilon^2_{t-i}}+\sum_{j=1}^{n}{\beta_j\sigma^2_{t-j}} \end{array}$$

• 单期：
  在模型估计的基础上，可以在最后一期预测下一期的收益率和波动率 $\hat x_T(1)，~\hat \sigma^2_T(1)$。进而在假定 $z_t$ 的分布的基础上，计算 $VaR_T(1)$ 和 $ES_T(1)$。

# P271：IBM股票
xt=-ibm                                                       # 计算多头损失率
library(fGarch)
m1=garchFit(~garch(1,1),data=xt,trace=F)
m1                                                            # P270估计结果
m1pre1=as.numeric(predict(m1,1))                              # 提前一步预测
source("RMeasure.R")
m11=RMeasure(mu=m1pre1[1],sigma=m1pre1[2])                             
m2=garchFit(~garch(1,1),data=xt,trace=F,cond.dist="std")      # 学生分布
m2                                                            # P271估计结果
m2pre1=as.numeric(predict(m2,1))  
m22=RMeasure(mu=m2pre1[1],sigma=m2pre1[2],cond.dist="std",
             df=as.numeric(m2@fit$coef[5]))                   # 与P271结果不符
# 用rugarch包复制结果
sgarch_n=ugarchspec(variance.model = list(model="sGARCH"), 
        mean.model = list(armaOrder=c(0,0),include.mean=T),
        distribution.model = "norm")                          # 正态分布
sgarch_n.fit=ugarchfit(spec=sgarch_n, data=xt)
sgarch_n.fcst = ugarchforecast(sgarch_n.fit, n.ahead=1)
xt_nsd=as.numeric(sgarch_n.fcst@forecast$sigmaFor) 
xt_nmn=as.numeric(sgarch_n.fit@fit$coef[1])
p=c(0.05,0.01); q=1-p
z=qnorm(q)
xt_VaR_n=xt_nmn+z*xt_nsd                                      
fz=dnorm(z)
xt_ES_n=xt_nmn+fz/p*xt_nsd                                    
data.frame(p, xt_VaR_n, xt_ES_n)                              # P270结果
sgarch_t=ugarchspec(variance.model = list(model="sGARCH"), 
        mean.model = list(armaOrder=c(0,0),include.mean=T),
        distribution.model = "std")                           # 学生分布
sgarch_t.fit=ugarchfit(spec=sgarch_t, data=xt)
sgarch_t.fcst = ugarchforecast(sgarch_t.fit, n.ahead=1)
xt_tsd=as.numeric(sgarch_t.fcst@forecast$sigmaFor) 
xt_tmn=as.numeric(sgarch_t.fit@fit$coef[1])
nu=as.numeric(sgarch_t.fit@fit$coef[5])
t=qt(q,nu)
xt_VaR_t=xt_tmn+ t*xt_tsd    
fz=dnorm(z); ft=dt(t,nu)
xt_ES_t=xt_tmn+ft/p*xt_tsd*(nu+t^2)/(nu-1)               
data.frame(p, xt_VaR_t, xt_ES_t)                              # P271结果

• 多期
  当 $z_t$ 服从正态分布时，在第 $t$ 的提前 $l$ 步预测的损失率服从正态分布，均值和方差为：
  $${\hat x_t}\left[ l \right] = \sum\limits_{i = 1}^l {{{\hat x}_t}\left( i \right)},~~Var\left( {{{\hat x}_t}\left[ l \right]} \right) = \sum\limits_{i = 1}^l {{\hat \sigma^2_t}\left( l \right)}$$
  但是当 $z_t$ 服从学生分布等非正态分布时，$x_t[l]$ 不服从学生分布，此时需要通过数值模拟计算 $VaR_t[l]$ 和 $ES_t[l]$。

# P274
M1=predict(m1,15)                                            # 正态分布
pmean=sum(M1$meanForecast)
pvar=sum((M1$meanError)^2)
pstd=sqrt(pvar)
M11=RMeasure(pmean,pstd)
# P275
vol=volatility(m2)                                           # 学生分布
a1=c(1.922*10^(-6),0.06448); b1=0.9286; mu=-4.113*10^(-4)
ini=c(ibm[2515],vol[2515])
set.seed(1)                     # 如果设不同的随机种子，结果与教材差别很大
source("SimGarcht.R")                                        # 模拟数据
mm=SimGarcht(h=15,mu=mu,alpha=a1,b1=b1,df=5.751,ini=ini,nter=30000)
rr=mm$rtn
mean(rr)
q=quantile(rr,c(0.95,0.99))                                  # VaR
idx=c(1:30000)[rr>q[1]] 
mean(rr[idx])                                                # ES_0.95
idx=c(1:30000)[rr>q[2]] 
mean(rr[idx])                                                # ES_0.99

2.2 基于分位数回归

• 样本分位数
  将损失率的样本数据从小到大排列：
  $$x_{(1)}\le x_{(2)}...\le x_{(T)}$$
  对于分位数 $0<q<1$，记 $L\le Tq \le H$（$H$ 和 $L$ 分别为满足这一条件的最小和最大整数），$q_H=H/T,~q_L=L/T$。$q$ 分位的样本估计值（即VaR）和ES分别为：
  $$\hat x_q = \widehat {VaR}_{1-p} = \frac{q_H-q}{q_H-q_L}x_L+\frac{q-q_L}{q_H-q_L}x_H\\ \widehat {ES}_{1-p}=\frac{{\sum\limits_{i = L + 1}^T {{x_{\left( i \right)}}} }}{{T - L}}$$

# P277：样本分位数
quantile(xt,0.95)
sxt=sort(xt) 
0.95*2515
es=sum(sxt[2390:2515])/(2515-2389)
es

• 分位数回归
  与一般的线性回归 $x=Z\beta + \varepsilon$ 不同，分位数回归的系数与解释变量 $Z$ 所处的分位数有关：
  $$\beta (q) = \text{argmin}~{\sum_{i}{w_q(x_i - Z_i \beta)}}\\ {w_q}\left( \varepsilon_i \right) = \left\{ {\begin{array}{*{20}{c}} {q\varepsilon_i ,~~~~~~~~~~~~~~~\varepsilon_i \ge 0}\\ {-\left( {1 - q} \right)\varepsilon_i ,~~\varepsilon_i < 0} \end{array}} \right.$$
  如果解释变量 $Z=1$，$\beta(q)$ 就是 $x$ 的分位数。否则 $\beta(q)$ 表示不同水平 的 $Z$ 对 $x$ 的影响不同，如收入对食品支出的分位数回归：
  

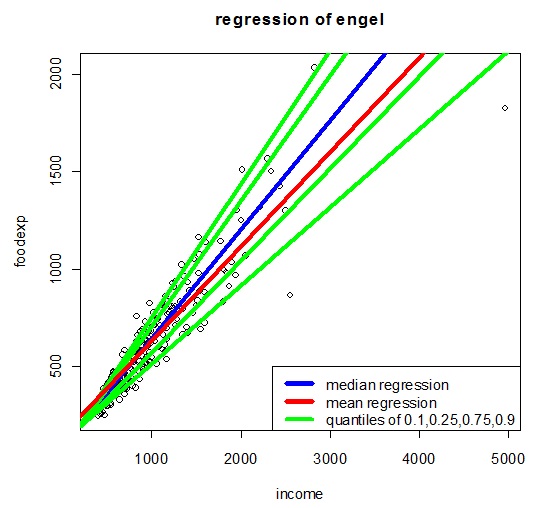
# P279：分位数回归 
dd=read.table("d-ibm-rq.txt",header=T) 
head(dd)
dd[,3]=dd[,3]/100
library(quantreg)
mm=rq(nibm~vol+vix,tau=0.95,data=dd)                       # q=0.95
summary(mm)
names(mm)
fit=mm$fitted.values
tdx=c(2:2515)/252+2001
plot(tdx,dd$nibm,type='l',xlab='year',ylab='neg-log-rtn')  # 图7-7
lines(tdx,fit,col='red')
mm=rq(xt~vol+vix,tau=0.99,data=dd)                         # q=0.99，与P280结果不同
summary(mm)

3. 极值理论

3.1 基本概念

极值理论（Extreme Value Theory, EVT）讨论 $T \to \infty$ 时服从独立同分布的随机变量的极大值 $x_{(T)}= \mathop {\max }\limits_{t = 1,2...T} \{ {x_t}\}$ 的统计性质。
根据 Fisher–Tippett–Gnedenko 定理，当 $T\to \infty$ 时，如果存在均值和标准差数列 $\left\{\mu_T\right\}\in \mathbb {R}$ 和 $\left\{\sigma_T\right\}>0$，使正规化的极大值随机变量 $X = \frac{{{x_T} - {\mu _T}}}{{{\sigma _T}}}$ 有渐进分布：$\mathop {\lim }\limits_{T \to \infty } {\rm{P}}\left( {X \le x} \right) = F(x)$
则称 $X$ 服从广义极值分布（Generalized Extreme Value, GEV），相应的累积分布函数为：

$$F\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {\exp \left[ { - {{(1 + \xi x)}^{ -1/\xi }}} \right],~~\xi \ne 0}\\ {\exp \left[ - \exp ( - x)\right],~~~~~~~~~\xi = 0} \end{array}} \right.$$
其中 $\mu = \lim_{T \to \infty}{\mu_T}$ 为位置参数(location parameter)；$\sigma = \lim_{T \to \infty}{\sigma_T}$ 为尺度参数 (scale parameter)；$\xi$ 为形状参数（shape parameter），控制极限分布的尾部行为，称 $1/\xi$ 为尾部指数（tail index）。相应的概率密度函数为：
$$f\left( x \right)= \left\{ {\begin{array}{*{20}{c}} {{{(1 + \xi x)}^{ - 1/\xi - 1}}\exp \left[ { - {{(1 + \xi x)}^{ - 1/\xi }}} \right],~\xi \ne 0}\\ {\exp [ - x - \exp ( - x)],~~~~~~~~~~~~~~~~~~~~~~~~~~\xi = 0} \end{array}} \right.$$
按照形状参数的取值范围，GEV又可分为三种类型：
1. 类型I：Gumbel 族，$\xi =0$
$$F\left( x \right)= \exp \left[ - \exp ( - x)\right],~~-\infty < x < \infty$$
2. 类型II：Frechet 族，$\xi >0$
$$F\left( x \right)= \left\{ {\begin{array}{*{20}{c}} {\exp \left[ { - {{(1 + \xi x)}^{ - 1/\xi }}} \right],~~x > - 1/\xi }\\ {0,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~x \le - 1/\xi } \end{array}} \right.{\rm{ }}$$
3. 类型III：Weibull 族，$\xi<0$
$$F\left( x \right)= \left\{ {\begin{array}{*{20}{c}} {\exp \left[ { - {{(1 + \xi x)}^{ - 1/\xi }}} \right],~~x < - 1/\xi }\\ {1,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~x \ge - 1/\xi } \end{array}} \right.{\rm{ }}$$

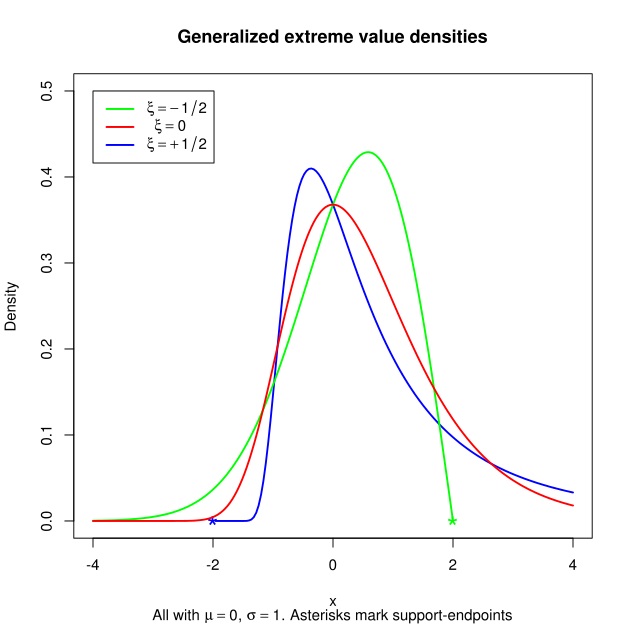
3.2 估计

极值分布的三个重要参数：形状参数 $\xi$（shape），位置参数 $\mu$（location） 和尺度参数 $\sigma$（scale）。

1. 分块经验估计
   将样本至少分为三块（$g>3$，每块平均有 $n$ 个样本，$T=ng$），分别估计三个参数。evir包中的gev命令就用这一方法。
2. 最大似然法
   根据密度函数构造似然函数，进而估计参数。这一估计是无偏、渐近正态的，并在适当假设下是渐近有效的。
3. 非参估计
   Hill(1975)和Pickands(1975)提出以下估计量（Q为正整数）：
   $$\xi_h(Q)=\frac{1}{Q}\sum_{i=1}^{Q}{[\text{ln}x_{(T-i+1)}-\text{ln}x_{(T-Q)}]}\\ \xi_p(Q)=\frac{1}{\text{ln}(2)}\text{ln}(\frac{x_{(T-Q+1)}-x_{(T-2Q+1)}}{x_{(T-2Q+1)}-x_{(T-4Q+1)}}),~Q\le T/4$$
   Hill 估计仅对Frechet族适用，但当它适用时，比Pickands估计更有效。

# P285表7-1第一列
source("Hill.R") # compile R script
Hill(ibm,110);  Hill(xt,110)             
# P286表7-2，子区间长度为21个交易日
library(evir)
gev(ibm,block=21)$par.ests               
gev(xt,block=21)$par.ests 
# P287图7-11
par(mfcol=c(1,2))
m1=gev(xt,block=21)
plot(m1)

3.3 应用

• 计算风险值 $VaR$
  
  • 单期：
    $$VaR = \left\{ {\begin{array}{*{20}{c}} {\mu - \frac{\sigma }{\xi }\left\{ {1 - {{\left[ { - n\ln \left( {1 - p} \right)} \right]}^{ - \xi }}} \right\},~~\xi \ne 0}\\ {\mu - \sigma \ln \left[ { - n\ln \left( {1 - p} \right)} \right],~~~~~~~~~~~~~~~~~\xi = 0} \end{array}} \right.$$
  • 多期，持有 $l$ 期和持有 1 期的风险值遵循 $\alpha$ 根法则。
    $$VaR(l)=l^{1/\alpha}VaR=l^{\xi}VaR$$
• 计算收益率水平 $L_{n,g}$（return level）
  假定有 $g$ 个长度为 $n$ 的子区间，其中有1个子区间的最大值超过 $L_{n,g}$，即：
  $$Pr[x_{n,i}>L_{n,g}]=\frac{1}{g}$$
• 计算超出门限的峰值（Peaks Over Threshold, POT）
  设定 $\eta$ 为损失率的门限，POT方法关注第 $i$ 次发生超过门限的巨大损失的时间 $t_i$ 和程度 $x_{t_i}-\eta$。根据POT理论，超额损失 $y=x_{t_i}-\eta$ 的极限累积分布为广义帕累托分布（Generalized Pareto Distribution, GPD），在估计GPD函数参数的基础上，也可以计算 VaR 和 ES。

# P291：收益率水平
m1=gev(xt,block=21)                        # n=21
rl.21.12=rlevel.gev(m1,k.block=12)         # g=12
rl.21.12                                   # L=5.43% in (4.65%,6.76%)           
# P293：图7-12
par(mfcol=c(2,1))
qplot(xt,threshold=0.01,pch='*',cex=0.8,main="Loss variable of daily IBM log returns")
meplot(ibm)
title(main="Daily IBM log returns")
# P294：表7-3
m1=pot(xt,threshold=0.01)            # pot命令
m1$par.ests
m2=pot(xt,threshold=0.012)
m2$par.ests
m3=pot(xt,threshold=0.008)
m3$par.ests
riskmeasures(m1,0.95)                # VaR和ES 
riskmeasures(m2,0.95) 
riskmeasures(m3,0.95) 
# P296  
m1gpd=gpd(xt,threshold=0.01)         # gpd命令
m1gpd
names(m1gpd)
par(mfcol=c(2,2))
plot(m1gpd)                          # 图7-13
riskmeasures(m1gpd,0.95)             # VaR和ES 

• 平稳损失过程
  考虑到严格平稳时间序列 $x_t$ 可能存在的时间相关性，需要对基于极值理论的VaR计算公式进行调整，其中 $\theta \in (0,1)$ 为极值指数：
  $$VaR = \left\{ {\begin{array}{*{20}{c}} {\mu - \frac{\sigma }{\xi }\left\{ {1 - {{\left[ { - n\theta\ln \left( {1 - p} \right)} \right]}^{ - \xi }}} \right\},~~\xi \ne 0}\\ {\mu - \sigma \ln \left[ { - n\theta\ln \left( {1 - p} \right)} \right],~~~~~~~~~~~~~~~~~\xi = 0} \end{array}} \right.$$

m1=exindex(xt,10)                                     # 图7-10
m1[which(m1[,2]==21),]                                # 子区间为21天，theta=0.725
1.966-(1.029/.251)*(1-(-21*.72*log(.99))^(-.251))     # VaR