第十六讲 系统性金融风险III：大数据分析方法简介与应用

樊潇彦 复旦大学经济学院 金融数据

---

1. 为什么需要大数据方法？

给定解释变量 $X$ 和被解释变量 $y$，传统计量经济学的方法是寻找参数 $\beta$，使样本估计值 $\hat y = f(X,\beta)$ “接近” 真实值 $y$，常用的准则是残差平方和(Residual Sum of Squares, RSS)最小。

• 以OLS估计为例，假定 $y = X\beta + \varepsilon$，在一定的条件下$\hat y = X\beta^{OLS}$，其中：
  $$\beta^{OLS}=\text{argmin}~{\varepsilon^T\varepsilon}=\left(X^TX\right)^{-1}X^Ty$$
• 当 $y\in \left\{1,2...K\right\}$ 为离散变量时，在一定的假定条件下，用Logit模型可以估计 $y=k$ 的概率：
  $$P(y=k)=\frac{exp(X\beta_k)}{\sum_k{exp(X\beta_k)}}$$

在大数据环境下，样本量(也称为观测数) $N$ 和解释变量的个数(也称为特征数) $K$ 都很大。当 $K>N$ 时称为高维数据，此时传统的计量经济学方法不再适用，需要有新的估计方法。

2. 金融和商业预测中常用的大数据方法

以下介绍借鉴了James et al.(2015)、Bajari et al.(2016)和Shi(2020)等。

2.1 支持向量机(support vector machines, SVM)

支持向量机估计量定义如下（损失函数 ${V_\Delta }\left( \varepsilon \right) = \max \left\{ {0,\left| \varepsilon \right| - \Delta } \right\}$，调节参数 $\lambda\ge 0$，$\bf{1}$为单位向量）：

$$\beta^{SVM}=\text{argmin}~{V_\Delta\left(y-X\beta\right)+\frac{\lambda}{2}\beta^T\bf{1}}$$

2.2 岭回归(Ridge regression)与套索回归(LASSO regression)

• 岭回归估计量定义如下（损失函数 $V\left( \varepsilon \right) = \varepsilon^T\varepsilon$，调节参数 $\lambda\ge 0$）：
  $$\beta^{RIDGE}=\text{argmin}~{V\left(y-X\beta\right)+\lambda\beta^T\beta}$$
• 套索回归估计量定义如下（损失函数 $V\left( \varepsilon \right) = \varepsilon^T\varepsilon$，调节参数 $\lambda\ge 0$，$\bf{1}$为单位向量）：
  $$\beta^{LASSO}=\text{argmin}~{V\left(y-X\beta\right)+\lambda\beta^T\bf{1}}$$

James et al.(2015)指出：“一般情况下当一小部分预测变量是真实有效的，而其他预测变量系数非常小或者等于零时，LASSO要更为出色；当响应变量是很多预测变量的函数，并且这些变量系数大致相等时，岭回归较为出色。”

2.3 基于树的回归方法(tree-based regression)

基于树的回归和分类方法是将预测变量空间划分为一系列简单区域，由于划分过程可以被概括为一棵树，因此也称为决策树(decision tree)方法。下面介绍最基本的回归树方法，以及袋装法、随机森林和提升法三种改进方法。

1. 回归树(regression tree)
根据Breiman et al.(1984)，回归树是传统的非参估计中核估计方法的替代形式(an alternative to kernel regression)。给定数据 $d$，建立回归树的过程可以分为两步：(1)将预测变量空间分割成 $J$ 个互不重叠的区域 $R_1,R_2,...R_J$；(2)对落入区域 $R_j$ 的每个观测值做同样的预测，预测值 $\hat y_{R_j}$ 等于$R_j$上训练集的响应值的简单算术平均。估计量为：

$$\hat y_{\text{tree}}(d)=\text{argmin} \sum_j^J{\sum_{i\in R_j}{\left(y_i-\hat y_{R_j}\right)^2}}$$

2. 袋装法(bagging, or bootstrap averaging)
回归树方法最大的缺点是不稳定，回归结果对树的深度(depth of the tree)和分叉标准非常敏感。Breiman(1996)提出的袋装法(bagging, or bootstrap averaging)可以有效地解决这一问题，思想是先选取$B$组自助样本(boostrap sample)，然后对每组样本数据进行回归树估计，最后求估计结果的均值。袋装法的估计量为：

$$\hat{y}_{\text{bagging}} = B^{-1} \sum_{b=1}^B \hat{y}( d^{\star b} ).$$

3. 随机森林(random forest)
Breiman(2001)提出的随机森林(random forest)方法也可以视为对回归树方法的一种改进，基本思想是每次在对树做分叉之前，先随机选出 $m$ 个解释变量，对剩下的变量做树的分叉，调节参数是树的深度和 $m$。

4. 提升树(tree boosting)
根据Shi(2020)的课件，提升树方法有三个调整参数：树深(the tree depth)、缩减参数(the shrinkage level，$\alpha$）和迭代次数 $M$，遵循以下步骤：

1. 令迭代次数 $m=0$，使用原始数据 $d^0=(x_i,y_i)$ 生成树 $\hat{y}^{0}(d^0)$，保存预测 $f^0_i=\alpha \cdot \hat{y}^0_i$，其中
   $\alpha \in [0,1]$ 是一个收缩调整参数。保存残差 $e_i^{0}= y_i - f^0_i$。更新 $m=1$。
2. 在第 $m$ 次迭代中，使用数据 $d^m=(x_i,e_i^{m-1})$ 来生成树 $\hat{y}^{m}(d^m)$。保存预测 $f^m_i = f^{m-1}_i + \alpha \cdot \hat{y}^m$。保存
   残差$e_i^{m}=y_i - f^m_i$。更新 $m=m+1$。
3. 重复步骤2，直到 $m>M$。

提升树方法可用gbm包实现，ShiLin et al.(2020) 用该方法分析和预测了北京的房价，得到了比OLS估计更好的样本外$R^2$，R程序可下载。

2.4 神经网络(neural network, NN)

Martin et al.(2013) 第19章给出了神经网络和AR(1)回归的关系：

$${y_t} = \underbrace {\phi {y_{t - 1}}}_{\text{Linear}} + \underbrace {\beta \left[ {\frac{1}{{1 + \exp \left( { - \left( {{\delta _0} + {\delta _1}{y_{t - 1}}} \right)} \right)}}} \right]}_{\text{Non-linear}} + {v_t}$$
下面是Martin et al.(2013)的表19.3，从中可以看到神经网络和计量经济学术语的联系：

Shi(2020)指出，从统计学家的角度来看神经网络是一种特殊类型的非线性模型。$k$ 层神经网络模型可以写成：

$$\begin{eqnarray} z_l^{(k)} & = & w_{l0}^{(k-1)} + \sum_{j=1}^{J_{k-1} } w_{lj}^{(k-1)} a_j^{(k-1)} \\ a_l^{(k)} & = & g^{(k)} ( z_l^{(k)})， \nonumber \end{eqnarray}$$

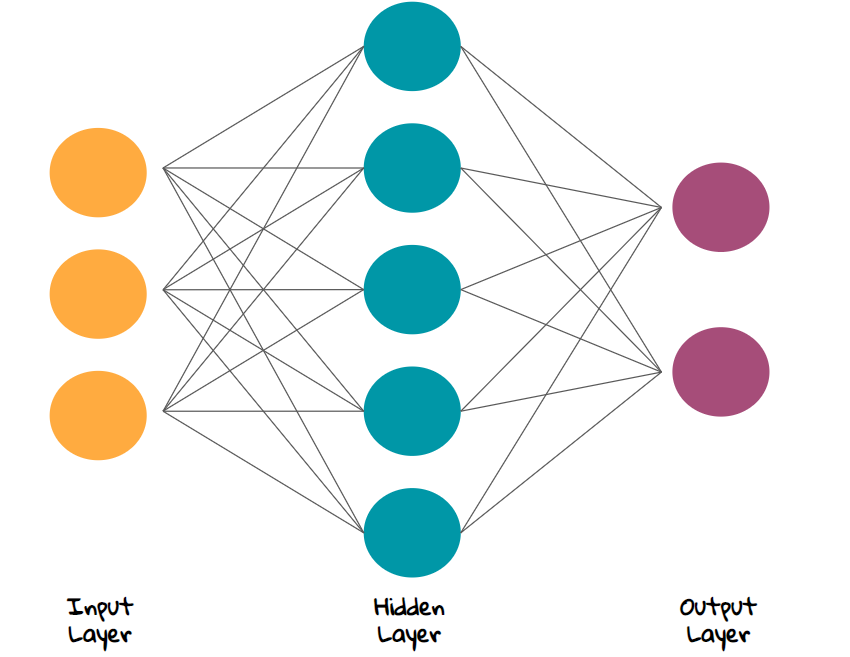
其中：

• 第 $k$ 个隐藏层(hidden layer) 有 $J_{k-1}$ 个输入$a_j^{(k-1)}, j=1,2,...J_{k-1}$，$a_j^{(0)}=x_j$ 为原始输入数据。
• $z_l^{(k)}$ 为第 $k$ 个隐藏层的输出，最后一层的输出为估计值 $\hat y_l = z_l^{(K)}$。$z_l^{(k)}$通常采用线性形式，所有的 $w$ 为待估计参数。
• 第 $k$ 层的输出经激活函数 $g(\cdot)$ 变换，成为下一层的输入。 激活函数可以是一个特征函数或一个简单的非线性函数，常用的选择有sigmoid函数 $1/(1+exp(-x))$ 或整流线性单元等。

神经网络的应用示例可参见Sanjiv Ranjan Das 在线教材。

3. 系统性风险分析的应用

3.1 Diebold and Yilmaz(2003)：风险溢出指数(SOI)

假定对均值为零的时序向量 $\mathbf{y_t}=\left(y_{1,t},y_{2,t}...y_{N,t}\right)^T$ 可以建立以下的VAR(1)模型：

$$\mathbf{y_t} = \mathbf{\Phi y_{t-1}}+ \varepsilon_t$$
残差协方差矩阵 $\Sigma_t=E\left(\varepsilon_t \varepsilon^T_t\right)$ 唯一的下三角Cholesky因子(unique lower‐triangular Cholesky factor)记为$\bf{Q_t}$，即 $\bf{Q_t}\bf{Q^T_t}=\Sigma_t$，上式可改写如下（ 其中$E\left(\bf{u_t}\bf{u^T_t}\right)=\bf{I}$ ）：
$${{\bf{Y}}_{\bf{t}}} = \underbrace {{{\left( {{\bf{I}} - {\bf{\Phi L}}} \right)}^{ - 1}}{{\bf{Q}}_{\bf{t}}}}_{{\bf{A}}\left( {\bf{L}} \right)}\underbrace {{{\bf{Q}}_{\bf{t}}}^{ - 1}{\varepsilon _t}}_{\bf{u_t}}$$
记 $E_t\left[\bf{y_{t+1}}\right]=\bf{y_{t+1,t}}=\mathbf{\Phi y_t}$，则对未来一期的预期误差(1-step-ahead error)等于：
$$\bf{e_{t+1,t}}=\bf{y_{t+1}}-\bf{y_{t+1,t}}=\bf{A_0u_{t+1}}$$
相应的方差(1‐step‐ahead error variances)矩阵：
$$E\left( {{e_{t + 1,t}}e_{t + 1,t}^T} \right) = {A_0}A_0^T = \left[ {\begin{array}{*{20}{c}} {a_{0,11}^2 + a_{0,12}^2}&{{a_{0,11}}{a_{0,21}} + {a_{0,12}}{a_{0,22}}}\\ {{a_{0,21}}{a_{0,11}} + {a_{0,22}}{a_{0,12}}}&{a_{0,21}^2 + a_{0,22}^2} \end{array}} \right]$$
定义自方差占比(own variance shares, OVS)和交叉方差占比(cross variance shares)，后者也称为溢出指数(spillover index, SOI)：
$$\begin{array}{l} OVS = 100 \times \frac{{a_{0,11}^2 + a_{0,22}^2}}{{trace\left( {{A_0}A_0^T} \right)}}\\ SOI = 100 \times \frac{{a_{0,12}^2 + a_{0,21}^2}}{{trace\left( {{A_0}A_0^T} \right)}} \end{array}$$
对于VAR(p)和多步向前预测(h-step-ahead forcast)，可以做类似定义。Klößner and Wagner(2009)提供了SOM程序，以及fastSOM包计算SOI，但运行速度很慢。

3.2 Barigozzi and Brownlees(2019)：风险溢出矩阵的LASSO估计

对均值为零的时序向量建立以下的VAR(p)模型（其中 ${\varepsilon _t} \sim i.i.d.\left( {0,{{\bf{C}}^{ - {\bf{1}}}}} \right)$，$\bf{C} = \Sigma^{-1}$为逆协方差矩阵）：

$$\mathbf{y_t} = \sum\limits_{k = 1}^p \mathbf{\bf{A}_k y_{t-k}}+ \varepsilon_t$$
对第 $i$ 个变量可以写为：
$${y_{it}} = \sum\limits_{k = 1}^p {\sum\limits_{j = 1}^n {{\alpha _{ijk}}{y_{j,t - k}}} } + {\varepsilon _{it}}$$
此外，设定同期方程（contemporaneous equations）：
$${\varepsilon _{it}} = \sum\limits_{h = 1, h \ne i}^n {{\rho ^{ih}}\sqrt {\frac{{{c_{hh}}}}{{{c_{ii}}}}} {\varepsilon _{h,t}}} + {u_{it}}$$
两式合并有：
$${y_{it}} = \sum\limits_{k = 1}^p {\sum\limits_{j = 1}^n {\underbrace {\left( {{\alpha _{ijk}} - \sum\limits_{l = 1,l \ne i}^n {{\rho ^{il}}\sqrt {\frac{{{c_{ll}}}}{{{c_{ii}}}}} {\alpha _{ljk}}} } \right)}_{{\beta _{ijk}}}{y_{j,t - k}}} } + \sum\limits_{h = 1,h \ne i}^n {\underbrace {{\rho ^{ih}}\sqrt {\frac{{{c_{hh}}}}{{{c_{ii}}}}} }_{{\gamma _{ih}}}{y_{h,t}}} + {u_{it}}$$
通过最小化损失函数 $V\left( {\theta ;{{\bf{y}}_{\bf{t}}},{\bf{C}}} \right) = \sum\limits_{i = 1}^n {{{\left( {{y_{it}} - {{\hat y}_{it}}} \right)}^2}}$ 估计参数 $\theta = \left(\bf{\alpha},\bf{\rho}\right)$：
$$\hat \theta = \arg \min V\left( {\theta ;{{\bf{y}}_{\bf{t}}},{\bf{C}}} \right)$$
显然，上述方法的待估参数的个数为 $n^2p+n(n-1)/2$，给定样本量当 $n$ 很大时无法得到一致估计，因此考虑下述LASSO回归方法：
$${{\hat \theta }^{LASSO}} = \arg \min \left[ {\frac{1}{T}\sum\limits_{t = 1}^T {V\left( {\theta ;{{\bf{y}}_{\bf{t}}},{{{\bf{\hat C}}}_T}} \right)} + \lambda _T^{\bf{G}}\sum\limits_{k = 1}^p {\sum\limits_{i,j = 1}^n {\frac{{\left| {{\alpha _{ijk}}} \right|}}{{\left| {{{\hat \alpha }_{Tijk}}} \right|}}} + \lambda _T^{\bf{C}}\sum\limits_{l,h = 1;. > h}^n {\frac{{\left| {{\rho ^{lh}}} \right|}}{{\left| {\hat \rho _T^{lh}} \right|}}} } } \right]$$

其中 $\lambda _T^{\bf{G}},\lambda _T^{\bf{C}}>0$ 是调节参数，$\hat \alpha _T,\bf{\hat C}_T$ 是通过回归VAR(p)方程得到的有偏估计量。利用偏相关系数的定义 ${\rho ^{ij}} = \text{corr}\left( {{\varepsilon _{it}},{\varepsilon _{jt}}|\left\{ {{\varepsilon _{kt}}:k \ne i,j} \right\}} \right) = - \frac{{{c_{ij}}}}{{\sqrt {{c_{ii}}{c_{jj}}} }}$ 可计算 $\hat \rho _T$。

显然，当 $\lambda _T^{\bf{G}},\lambda _T^{\bf{C}}$ 很大时，LASSO估计会把 $\hat \alpha _T,\hat \rho _T$ 中很小的参数变为零，最终得到的关联网络 $\hat\alpha, \hat\rho$ 会变得非常稀疏，从而可以更好地展示节点之间的关键作用。Browness提供了nets包以及示例程序。

4. 补充阅读材料

• Gu et al.(2020)调查了1957年至2016年交易的3万只个股，利用机器学习(ML)的几种技术研究了数百种可能的预测信号，结果发现在这项具有挑战性的任务中，ML比传统分析有显著优势。Chicago Booth Review总结了文章的几个主要发现:(1)决策树和神经网络是预测资产价格最有效的ML形式。使用决策树，计算机学会以扩张性流程图的方式进行思考，并进行多次迭代。神经网旨在模仿生物神经网络，这种技术在模拟非线性和互动模式方面特别有用。(2)在研究人员调查的近100个特征中，最成功的预测因素是价格趋势、流动性和波动性。(3)机器在预测大的、流动性强的股票的风险溢价方面比预测小的、流动性较差的股票要好。Matlab程序和数据可从Dacheng Xiu 的个人主页下载。

• Das, S.R. 2017: Data Science: Theories, Models, Algorithms, and Analytics, Online textbook

参考文献

1. Bajari, P., D. Nekipelov, S.P. Ryan, and M.Y. Yang 2015: Machine learning methods for demand estimation, American Economic Review, Vol.105(5), P481–85
2. Barigozzi, M. and C. Brownlees 2019: NETS: Network estimation for time series, Vol.34(3), P347-364， R package: nets
3. Diebold, F.X. and K. Yilmaz 2009: Measuring Financial Asset Return and Volatility Spillovers, with Application to Global Equity Markets, The Economic Journal, Vol.119(534), P158-171
4. Gu, S.H., B. Kelly, and D.C. Xiu 2020: Empirical asset pricing via Machine Learning, Review of Financial Studies, Vol.33(5), P2223-2273
5. James, G., D. Vitten, T. Hastie, R. Tibshirani 著：《统计学习导论：基于R应用》，王星译，机械工业出版社，2015，（在线课程链接）
6. Klößner, S. and S. Wagner 2009: Exploring All Var Orderings For Calculating Spillovers? Yes, We Can! — A Note On Diebold And Yilmaz(2009), Journal of Applied Econometrics, Vol.29(1), P172-179, Data and Code
7. Lin, W., Z.T. Shi, Y.S. Wang, and T.H. Yan 2020, Unfolding Beijing in a Hedonic Way, Working Paper
8. Martin, V., A. Hurn, and D. Harris 2013: Econometric modelling with time series: specification, estimation and testing(Themes in Modern Econometrics), Cambridge University Press, United States of America
9. Shi, Z.T. 2020: Prediction-oriented algorithms, Lecture Notes in Computational Methods in Economics(Econ5170, CUHK)