第十四讲 系统性金融风险I：基本概念与统计度量

金融数据 樊潇彦 复旦大学经济学院

---

1. 系统性风险研究发展的历史背景与基本概念

1.1 为什么系统性风险研究很重要？

下图来自2011年国际清算银行年报（中文版），从中可以看到在雷曼兄弟倒闭之前，市场信号已经有所反映，但最终还是没能有效预测和防范金融危机的爆发。

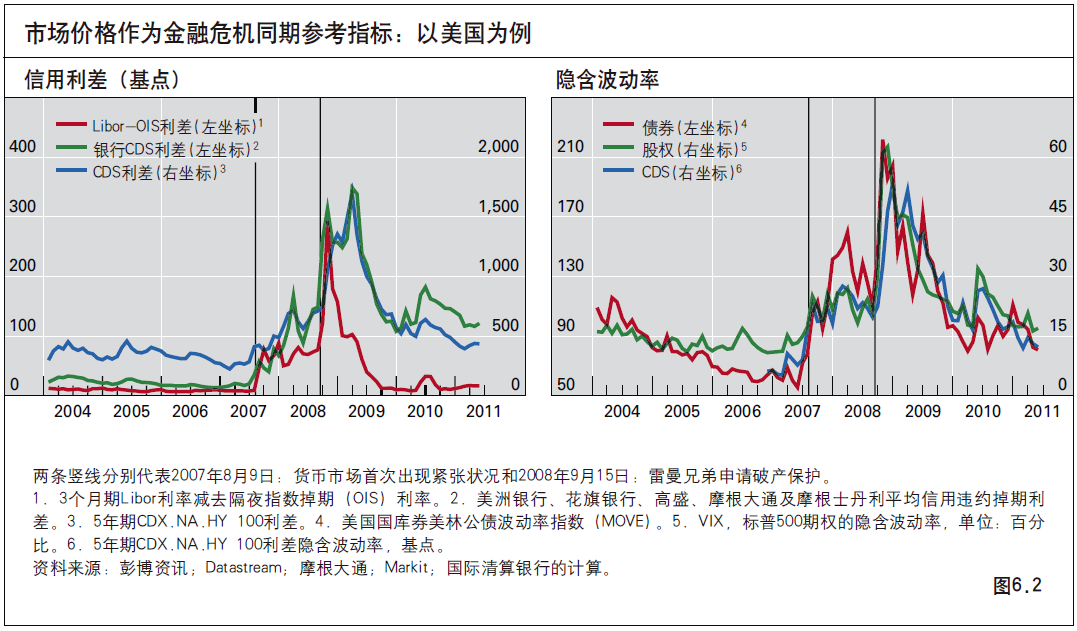
2008年金融危机之后，2010年7月美国国会通过了《多德-弗兰克华尔街改革与消费者保护法案》(Dodd-Frank Act)，这是自上世纪30年代以来最全面的金融改革法案。除此之外，《多德-弗兰克法案》还创建了金融稳定监督委员会(FSOC，简称金监会)和金融研究办公室(OFR，简称金研办)，形成了西方发达国家监管和防范系统性金融风险的标准组织架构。其中金监会有三大职责:

• 确定大型金融公司或其他方面的事件或活动对金融稳定造成的风险；
• 通过消除参与者对政府可能的救市预期，促进市场纪律；
• 对金融系统稳定所面临的新威胁作出反应。

但所有政策层面的工作都必须以理论层面对系统性风险的深入理解，以及实证层面对系统性风险的准确及时的度量为基础，因此对系统性风险的建模、分析和预测已经成为金研办的主要努力方向。

1.2 什么是系统性风险？

• Bisias et al.(2012)指出，系统性风险往往被视为“难以定义，但当你看到它时，你就会知道它”(hard-to-define-but-you-know-it-when-you-see-it)的概念。
• Billio et al.(2012)将系统性风险定义为"威胁到金融体系的稳定性或公众信心的任何情况"。
• ECB(2009)将系统性风险广义地定义为“严重的金融不稳定的风险”，也就是“金融不稳定变得非常普遍，以至于影响到金融系统的运作，并对经济增长和福利造成重大影响”的情况。

1.3 研究系统性风险的文献分类

Benoit et al.(2017)回顾了过去35年来发表的系统性风险方面的220篇论文，文献之间的引用关系如下图所示（其中圆圈的大小表示被其他文章引用的次数，列出了被引用次数最多的34篇论文）：

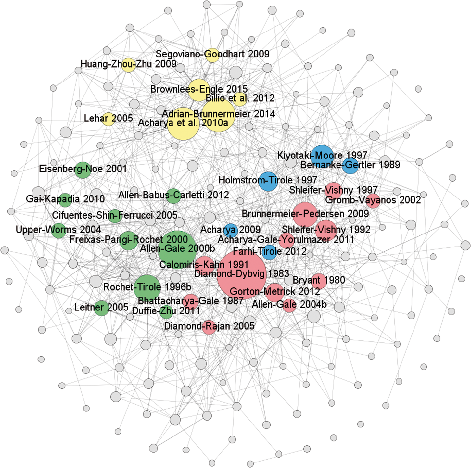
1. 按照研究主题，Benoit et al.(2017)将系统性风险的文献分为四个类别：

• 产生机制（蓝色/右侧）：金融摩擦、信用约束、信息问题等；
• 放大机制（红色/底部）：资产甩卖(fire-sell)、羊群效应、市场恐慌等；
• 传染机制（绿色/左侧）：机构间融资、相互担保与持股、相同的资产组合等；
• 度量方法（黄色/顶部）：SES，SRISK和∆CoVaR等。

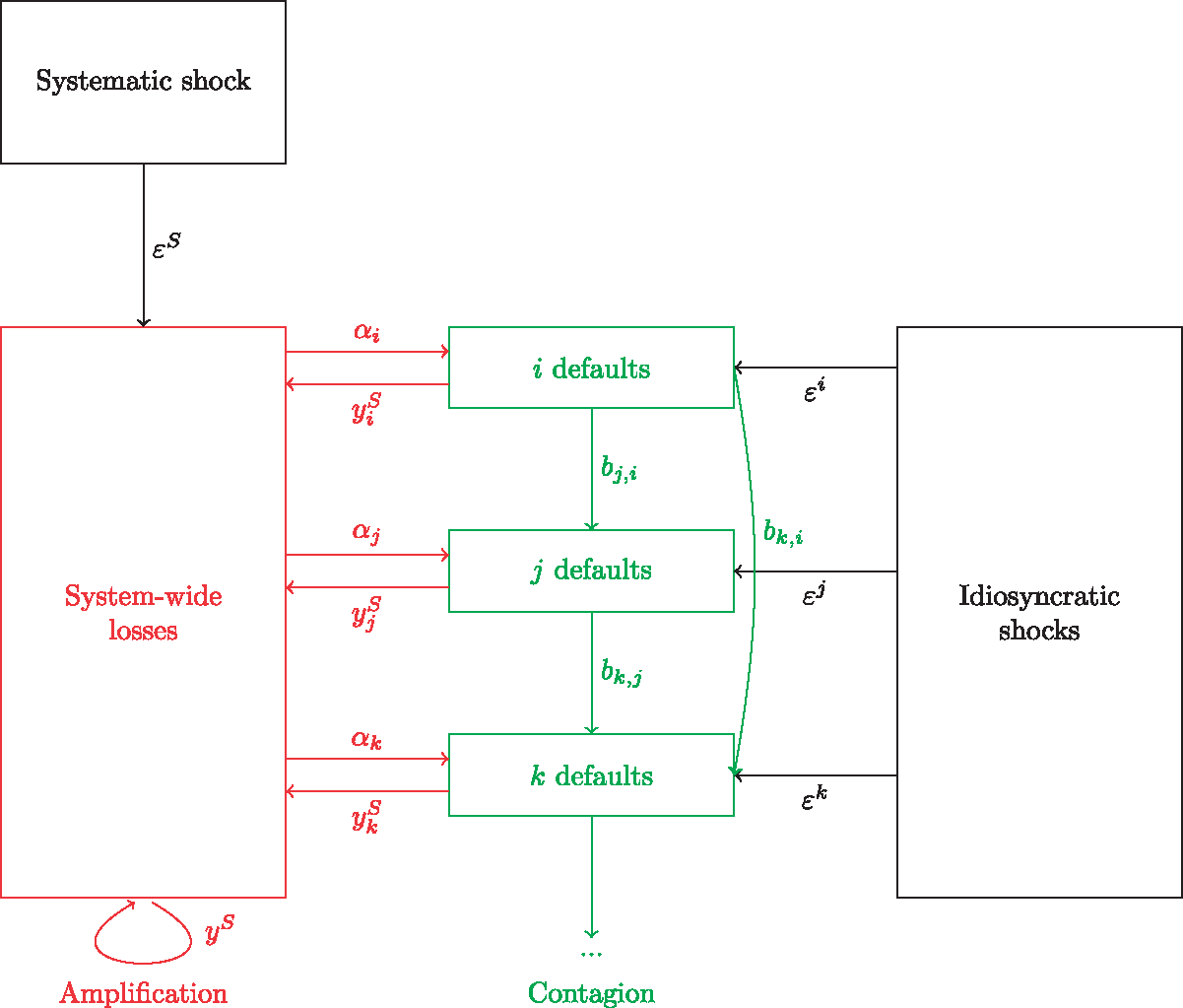
2. 按照分析方法和数据性质的差异，把文献分为两类：

• 全局性研究(global approach)：没有特定的理论基础和机制描述，相应的实证研究是基于公开的市场数据(market data)进行统计分析和预测，可能对潜在的系统性风险进行有效的预测和预警，以协助监管。比如现在几种主要的度量方法（SES，SRISK和∆CoVaR）都与市场风险值 $\beta$ 或 $VaR$ 呈正比，因此只是市场风险或风险极值的度量。由于它们本质上是统计指标，没有清楚的理论基础，不能解释指标的具体含义和影响因素，也很难为监管者提供更多信息和更有针对性的操作指引。优点是利用公开的市场交易数据和通用的统计计量方法就可以计算。
• 特定来源研究(source-specific approach)：分析系统性风险的某种特定的来源和作用机制，相应的实证研究需要使用金融机构的微观数据，有时甚至需要机构间融资和业务往来的保密数据，最后提出有针对性但复杂的监管工具。这种基于监管数据(regulatory data)的研究有理论基础，是一种结构性指标，对政策评估更有可借鉴性。缺点是数据一般是保密的，而且时效性很差。

2. 系统性风险的统计度量

2.1 度量原则

弗雷克萨斯等(2017)指出，识别和量化系统性风险的各种渠道一直是个难题，现有的系统性风险的测度尚处于早期阶段，我们不仅缺乏合适的系统性风险测度方法，也缺少进行正确测量所必须的数据。虽然目前监管者、学者和从业者尚未就如何定义和度量系统性风险达成广泛的共识，但仍有一些普遍接受的准则：

• 系统性风险的度量需要考虑两个维度的问题：（1）在时间维度，应该能够识别和量化金融风险的演变轨迹，并做出系统性风险的预警；（2）在横截面维度，需要识别和评价核心机构的作用和状况，并进行有针对性的监管和处理。
• Giglio et al.(2016)的实证比较研究发现，目前各指标都能较好地反映过去危机的发生，但预测能力强差人意。显然，要捕捉金融体系的复杂性和适应性，就需要不止一种风险衡量方法。由于各指标一般只关注于某一方面的变化，因此兼容并蓄、综合考量是更为稳妥、有效的办法。
• 各国金融监管机构和区域性、世界性组织应团结合作，加强信息披露与共享、加强政府沟通与协调。

下面我们简要介绍SES，SRISK和∆CoVaR三种最常用的系统性风险统计指标，其他基于金融网络的结构性度量指标将在第十五、基于大数据的度量方法在第十六讲中介绍。

2.2 常用统计指标

1. Acharya et al.(2017)：MES和SES
Acharya et al.(2017)在他们2010年的工作论文中提出，市场整体的期望损失(ES)是个股损失的加权：

$$ES_{\alpha}=-\sum_i w_iE\left(r_i|R\le-VaR_{\alpha}\right)$$
因此可定义个股的边际期望损失(Marginal Expected Shortfall, MES)，即如果增加1%的个股权重将导致市场整体风险上升多少：
$$MES^i_{\alpha}=\frac{\partial ES_{\alpha}}{\partial w_i}=-E\left(r_i|R\le-VaR_{\alpha}\right)$$
类似地，首先定义市场的系统性风险(systemic risk)为未来 $T$ 期市场累计回报率低于某个阈值（例如可设定 $T$ 为6个月，$\alpha = -40\%$）：
$$Crisis_{m,t:t+T}:=\left\{ {R_{m,t:t + T}} = \exp \left( {\sum\limits_{s = 1}^T {{r_{m,t + s}}} } \right) - 1 <\alpha \right\}$$
其次定义公司 $i$ 在危机中的预计资本缺口（capital shortfall）等于最低法定资本金与市值之差的期望值（其中 $k =8\%$ 为稳健性资本充足率，$A$ 和 $W$ 分别为资产市值和股票市值）：
$${CS_{i,t:t + T}} = {E_t}\left[ {k{A_{i,t + T}} - {W_{i,t + T}}\left| {Crisi{s_{m,t:t + T}}} \right.} \right]$$
显然，市场整体的资本缺口是个股资本缺口的加权值：
$$SES_{m,t:t + T}=\sum_i w_iE\left(CS_{i,t:t + T}|Crisis_{m,t:t+T}\right)$$
因此可定义：
$$MES_{i,t:t + T}=\frac{\partial SES_{m,t:t + T}}{\partial w_i}=E\left(CS_{i,t:t + T}|Crisis_{m,t:t+T}\right)$$
显然，如果一家公司很可能在金融行业出现问题的时候遭遇资金危机，那么这家公司存在系统性风险。

2. Brownlees and Engle(2017)：SRISK
在Acharya et al.(2017)的基础上，Brownlees and Engle(2017)提出公司 $i$ 的系统性风险（Systemic Risk Measure，SRISK）指标，衡量该公司在金融危机中的预计资本损失:

$$SRIS{K_{i,t:t + T}} = \max\left\{CS_{i,t:t + T},0\right\}$$
由于公司负债 $D = A - W$，因此 $CS_{i,t:t + T}>0$ 时有：
$$\begin{array}{l} SRIS{K_{i,t:t + T}} = {E_t}\left[ {k{D_{i,t + T}} - \left( {1 - k} \right){W_{i,t + T}}\left| {Crisi{s_{m,t:t + T}}} \right.} \right]\\ ~~~~~~~~~~~~~~~~~~~~~~~ = k{E_t}\left[ {{D_{i,t + T}}\left| {Crisi{s_{m,t:t + T}}} \right.} \right] - \left( {1 - k} \right){E_t}\left[ {{W_{i,t + T}}\left| {Crisi{s_{m,t:t + T}}} \right.} \right] \end{array}$$
对于第一项，由于是否发生危机不影响公司负债的账面价值，因此有 ${E_t}\left[ {{D_{i,t + T}}\left| {Crisi{s_{m,t:t + T}}} \right.} \right]=D_{i,t}$；对于第二项，定义危机情况下公司的长期边际预期损失（long-run marginal expected shortfall）为：
$$LRME{S_{i,t:t + T}} = {E_t}\left[ {1 - \frac{{{W_{i,t + T}}}}{{{W_{i,t}}}}\left| {Crisi{s_{m,t:t + T}}} \right.} \right]$$
代入第二项有 ${E_t}\left[ {{W_{i,t + T}}\left| {Crisi{s_{m,t:t + T}}} \right.} \right] = {E_t}\left[ {\left( {1 - LRME{S_{i,t:t + T}}} \right){W_{i,t}}\left| {Crisi{s_{m,t:t + T}}} \right.} \right]$。根据Brownlees and Engle (2017)，在一定的条件下，长期边际预期损失可以近似取值为 ${LRMES_{i,t:t + T}}= 1-\exp(\beta_{i,t}\ln(1-\alpha))$。因此最终有：
$$SRIS{K_{i,t}} = k \cdot {D_{i,t}} - \left( {1 - k} \right){W_{i,t}}\left( {1 - LRMES_{i,t}} \right)$$
为了看清SRISK的经济含义，对 $SRISK_{i,t}$ 求全微分：
$$dSRISK_i=k\cdot dD_i-(1-k)(1-LRMES_{i,t}) \cdot dW_i + (1-k)W_{i,t} \cdot dLRMES_i$$
因此，公司负债、市值和LRMES对SRISK的影响为：

• $dSRISK_i/dD_i = k >0$: 负债变化对SRISK的影响为正，负债上升将提高SRISK。
• $dSRISK_i/dW_i =-(1-k)(1-LRMES_{i,t})<0$: 资本金变化对SRISK的影响为负，市值下跌将提高SRISK。
• $dSRISK_i/dLRMES_i=(1-k)W_{i,t}>0$：风险属性增加（$d\beta_i>0$）对SRISK的影响为正。

3. Adrian and Brunnermeier(2016)：$\Delta CoVaR$
在个股在险值的基础上，Adrian and Brunnermeier(2016)提出变化的条件在险值(the Delta Conditional Value-at-Risk, ΔCoVaR)指标。给定个股的在险值 $Var^i_q$，定义市场 $m$ 对个股 $i$ 的条件在险值 $CoVar^{m|i}_q$，即如果个股大跌市场也大跌的话，那么跌幅度会是多少：

$$Pr\left[r_m \le CoVaR^{m|i}_q|r_i=VaR^i_q\right]=q$$
最后定义变化的条件在险值，即市场跌幅与 $q=0.5$ 时的跌幅相比大多少：
$$\Delta CoVar^{m|i}_q = CoVar^{m|i}_q-CoVar^{m|i}_{0.5}$$

2.3 R语言实现

1. 准备工作

setwd("D:\\...\\Ch14")
rm(list=ls())
install.packages("rmgarch","plotrix")
## 调用
library(rmgarch)
library(rugarch)
library(tidyverse)
library(readxl)
library(ggplot2)

以下是对Benoit et al.(2017)原始数据的处理，不用运行：

## 文中说时间为2000.1.3至2010.12.31，任意下载一个金融数据，取其时间标记
library(quantmod)
loadSymbols("MSFT", from ="2000-01-03", to = "2011-01-02") 
data=read_xls("Data_RMC.xls")%>%
  rename(rm=index,ri=asset)%>%                 # 参见 main_script.m 指标说明
  mutate(time=index(MSFT),
         rm=rm-mean(rm),ri=ri-mean(ri))%>%     # 去除均值，参见 call_ftc.m %demeaned returns
  select(time,rm:mv)
save(data,file="data.RData")

下载数据：Ch14_data.RData，读取并做图：

load("Ch14_data.RData")
str(data)
# time: from 2000.1.3 to 2010.12.31, daily data
# rm: Returns of the market (system)
# ri: Returns of the firm's equity
# ltq: Total amount of liabilities
# mv: Market Capitalisation
library(xts)
ret=xts(data[,2:3], order.by=data$time)
# 作图
plot(ret$rm, main="Returns of the market (system)")   
plot(ret$ri, main="Returns of the firm's equity")     
plot(coredata(ret$rm), coredata(ret$ri), xlab="rm", ylab="ri",
      type="p", pch=16, lwd=2, col="blue")
abline(h=0,v=0)

2. DCC-GARCH模型估计
以下参照Eric Zivot 课程程序：

library(rugarch)
library(rmgarch)
# univariate normal GARCH(1,1) for each series
garch11.spec = ugarchspec(mean.model = list(armaOrder = c(0,0)), 
                          variance.model = list(garchOrder = c(1,1),
                                                model = "gjrGARCH"), 
                          distribution.model = "std")  # "norm", "sstd"
# dcc specification - GARCH(1,1) for conditional correlations
dcc.garch11.spec = dccspec(uspec = multispec( replicate(2, garch11.spec) ), 
                           dccOrder = c(1,1), 
                           distribution = "mvnorm")
dcc.garch11.spec
dcc.fit = dccfit(dcc.garch11.spec, data = ret)
dcc.fit               # show dcc fit
# Make a plot selection (or 0 to exit): 
#   
# 1:   Conditional Mean (vs Realized Returns)
# 2:   Conditional Sigma (vs Realized Absolute Returns)
# 3:   Conditional Covariance
# 4:   Conditional Correlation
# 5:   EW Portfolio Plot with conditional density VaR limits
plot(dcc.fit, which=2)
plot(dcc.fit, which=4)
# class(dcc.fit)
# slotNames(dcc.fit)
# names(dcc.fit@mfit)           # many extractor functions
# names(dcc.fit@model)
ht_m=sqrt(dcc.fit@mfit$H[1,1,]) # market conditional volatility
plot(ht_m,type="l")
ht_i=sqrt(dcc.fit@mfit$H[2,2,]) # asset conditional volatility
plot(ht_i,type="l")
rho=rcor(dcc.fit)[1,2,]         # conditional correlation
plot(rho,type="l")

3. 计算MES、SRISK和dCoVaR
以下根据 Sylvain Benoit 提供的 Matlab 程序改写：

alpha = 0.05                    # Risk level of our VaR
k = 0.08                        # Prudential Capital Required (k*LTQ)
# Conditional Asset VaR from dcc with Empirical Quantile at alpha
Asset_VaR = ht_i*quantile(data$ri/ht_i,alpha)
# Conditional Market VaR from dcc with Empirical Quantile at alpha
Market_VaR = ht_m*quantile(data$rm/ht_m,alpha)
# Conditional beta
Beta = rho*ht_i/ht_m
c = quantile(data$rm,alpha)      # HS VaR (nonparametric)
## MES、LRMES和SRISK
fct_MES=function(data,c,ht_m,ht_i,rho){
  em=data$rm/ht_m                        #  market first column
  xi=(data$ri/ht_i-rho*em)/sqrt(1-rho^2) #  asset second column
  bwd=nrow(data)^(-0.2)                  #  Scaillet's bwd p21
  K1=sum(em*pnorm((c/ht_m-em)/bwd))/sum(pnorm(c/ht_m-em)/bwd)
  K2=sum(xi*pnorm((c/ht_m-em)/bwd))/sum(pnorm(c/ht_m-em)/bwd)
  MES = (ht_i*rho*K1) + (ht_i*sqrt(1-rho^2)*K2)
  return(-MES)
}
MES=fct_MES(data,c,ht_m,ht_i,rho)
plot(MES,type="l")    
LRMES = 1-exp(-18*MES)             # without simulation
SRISK = k*data$ltq - (1-k)*(1-LRMES)*data$mv 
plot(SRISK,type="l")
## 两种方法计算 Delta_CoVaR
gam = rho*ht_m/ht_i
Delta_CoVaR_dcc = - gam *(Asset_VaR-median(data$ri))
mean(Delta_CoVaR_dcc)              # Average DCoVaR(DCC)
plot(Delta_CoVaR_dcc,type="l") 
library(quantreg)    
CoVaR_rq=rq(data$ri~data$rm,alpha) # Quant with constant
gam_quant = CoVaR_rq$coefficients[2]
Delta_CoVaR_quant = - gam_quant*(Asset_VaR-median(data$ri))   
mean(Delta_CoVaR_quant)            # Average DCoVaR (quantile regression)
plot(Delta_CoVaR_quant,type="l") 
## 比较MES和DCoVaR(DCC)
com_all=data.frame(time=data$time,MES=MES, Delta_CoVaR_dcc=Delta_CoVaR_dcc)
library(plotrix)
twoord.plot(lx = com_all$time, ly = com_all$MES,
            rx = com_all$time, ry = com_all$Delta_CoVaR_dcc,
            main = "MES vs. DCoVaR(DCC)", xlab ="", 
            ylab = "MES", rylab = "DCoVaR(DCC)", type = c("l","l"))

3. 我国对系统性金融风险的监管和研究

下图是中国人民银行在《中国金融稳定报告（2008）》中提出的管理框架：

不难看出，我国对系统性金融风险的监管，主要包括事先加强制度建设和事后进行应对性管理两个方面，但对于事先进行有效可信的预测，以及事后制定科学量化的救助方案等具体操作层面，仍然缺乏坚实有效的科研支持。

目前我国学者在系统性风险方面的研究主要包括以下几方面：

• 方法介绍和文献综述：胡海峰和代松(2012)、王博和齐炎龙(2015)等；
• 研究具体的传播和放大机制：贾彦东(2011)、方意(2016)等；
• 针对银行系统的研究：王擎和田娇(2016)、唐文进和苏帆(2017)等；
• 宏观审慎监管与货币政策：周小川(2012)、童中文等(2017)等。

参考文献

1. Acharya, V.V., L.H. Pedersen, T. Philippon, and M. Richardson, 2017: Measuring systemic risk, Review of Financial Studies, Vol.30(1), P2-47
2. Adrian, T. and M.K. Brunnermeier 2016: CoVaR, American Economic Review, Vol.106(7), P1705-1741
3. Benoit, S., Colliard, J. E., Hurlin, C., and C. Pérignon 2017: Where the risks lie: A survey on systemic risk, Review of Finance, 21 (1): 109-152
4. Billio, M., M. Getmansky, A.W. Lo, and L. Pelizzon, 2012:Econometric measures of connectedness and systemic risk in the finance and insurance sectors, Journal of Financial Economics, Vol.104(3), P535-559
5. Bisias, D., Flood, M., Lo, A. W., and S. Valavanis 2012: A survey of systemic risk analytics, Annual Review of Financial Economics, Vol.4(1), P255-296
6. European Central Bank, 2009：The concept of systemic risk, Financial Stability Review (December 2009)
7. Giglio, S., B. Kelly, and S. Pruitt, 2016: Systemic risk and the macroeconomy: An empirical evaluation, Journal of Financial Economics, Vol.119(3), P457-471
8. X. 弗雷克萨斯、L. 莱文、J.L. 佩德罗著：《系统性风险、危机与宏观审慎监管》，王擎等译，中国金融出版社，2017
9. 周小川著：《国际金融危机：观察、分析与应对》，中国金融出版社，2012
10. 方意，2016：系统性风险的传染渠道与度量研究——兼论宏观审慎政策实施，《管理世界》，2016.8
11. 胡海峰、代松，2012：后金融危机时代系统性风险及其测度评述，《经济学动态》，2012.4
12. 贾彦东，2011：金融机构的系统重要性分析——金融网络中的系统风险衡量与成本分担，《金融研究》，2011.10
13. 唐文进、苏帆，2017：极端金融事件对系统性风险的影响分析——以中国银行部门为例，《经济研究》，2017.4
14. 童中文、范从来、朱辰、张炜，2017：金融审慎监管与货币政策的协同效应——考虑金融系统性风险防范，《金融研究》，2017.3
15. 王博、齐炎龙，2015：宏观金融风险测度:方法、争论与前沿进展，《经济学动态》，2015.4
16. 王擎、田娇，2016：银行资本监管与系统性金融风险传递——基于DSGE模型的分析，《中国社会科学》，2016.3