第四讲 概率统计与资产收益率

樊潇彦 复旦大学经济学院 金融数据

---

0. 准备工作

下载数据：price.Rdata

setwd("D:\\...\\Ch04")          # 设定工作目录，注意为/或\\
rm(list=ls())                   # 清内存
install.packages(c("MASS","Himsc","fBasics","mice","sm","mnormt"))
## 调用
library(tidyverse)
library(ggplot2)
library(MASS)
library(Himsc)
library(fBasics)
library(mice)
library(sm)
library(mnormt)

1. 概率统计基本概念

1.1 概率空间和概率

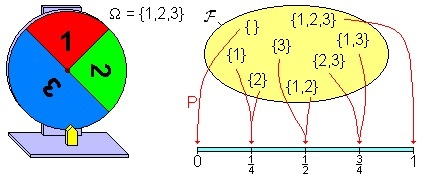
Source：Wiki term "Probability measure".

若函数 $P: \mathscr{F} \to \left[0,1\right]$ 满足：

• 非负性 $P\left(A\right) \ge 0$；
• 规一性 $P\left(\Omega\right)=1$；
• 可列可加性，即如果 $A_i \in \mathscr{F}$ 且 ${A_i}{A_j} = \emptyset ,(i \ne j)$
  则称 $P$ 为可测空间 $\left(\Omega,\mathscr{F}\right)$ 上的一个概率测度（probability measure），简称概率。

1.2 随机变量

• 定义：
  如果定义在样本空间上的实值函数 $X: \Omega \to \mathbb{R}$ 对任意 $x \in \mathbb{R}$ 有：
  $$\left\{\omega: X\left(\omega\right) \le x\right\} \in \mathscr{F}$$
  则称 $X$ 为 $\left(\Omega,\mathscr{F},P\right)$ 上的随机变量。
• 分类：
  
  • 离散型随机变量：如二项分布（伯努利分布，binom）、泊松分布pois等
  • 连续型随机变量：如均匀分布unif、正态分布（高斯分布，norm）、指数分布exp，以及$t$、$F$、$\chi^{2}$（t、F、chisq）分布等。
• 累积分布函数 $F: \mathbb{R} \to \left[0,1\right]$：
  $X$ 是概率空间 $\left(\Omega,\mathscr{F},P\right)$ 上的随机变量，若对于 $\forall x \in \mathbb{R}$ 存在：
  $$F\left(x\right) = P\left(X \le x\right)$$
  则称 $F: \mathbb{R} \to \left[0,1\right]$ 为累积分布函数（cumulative distribution function，cdf）。
• 概率密度函数 $f: \mathbb{R} \to \left[0, \infty \right)$：对连续随机变量 $X$，如果除有限个点外存在：
  $$f\left( x \right) = \frac{{dF}}{{dx}},~~~~\int_{ - \infty }^x {f\left( u \right)du} = P\left( {X \le x} \right) = F\left( x \right)$$
  称 $f: \mathbb{R} \to \left[0, \infty \right)$ 为概率密度函数（probability density function，pdf）。
• 频率函数或分布律：对于离散随机变量 $X \in \left\{x_i\right\}^N_{i=1}$，称 $p\left(x_i\right) = P\left(X = x_i\right)$ 为频率函数（frequency function）或分布律。

1.3 样本统计量

$\left\{x_t\right\}^T_{t=1}$ 是随机变量 $X$ 的 $T$ 个独立抽取的样本，常用的样本统计量（sample statistics）定义如下：

1. 样本均值（sample mean）：
   $$\hat \mu_x = \frac{1}{T}\sum\limits_{t = 1}^T {{x_t}}$$
2. 样本方差/标准差（sample variance / standard deviation）：
   $$\hat \sigma^2_x = \frac{1}{T-1}\sum\limits_{t = 1}^T {{{\left( {{x_t} - \hat \mu_x} \right)}^2}}$$
3. 样本偏度（sample skewness）：
   $$\hat S_x = \frac{1}{(T-1)\hat \sigma ^3_x}\sum\limits_{t = 1}^T {{{\left( {{x_t} - \hat \mu_x} \right)}^3}}$$
4. 样本峰度（sample kurtosis）：
   $$\hat K_x = \frac{1}{(T-1)\hat \sigma ^4_x}\sum\limits_{t = 1}^T {{{\left( {{x_t} - \hat \mu_x} \right)}^4}}$$

此外，假定 $\left\{y_i\right\}^N_{i=1}$ 是随机变量 $Y$ 的 $N$ 个独立抽取的样本，定义：

1. 协方差（covariance）：
   $$Cov_{xy} = \frac{1}{{N - 1}}\sum\limits_{i = 1}^N {\left( {{x_i} - {{\hat \mu }_x}} \right)\left( {{y_i} - {{\hat \mu }_y}} \right)}$$
2. 相关系数（correlation coefficient）：
   $${\rho _{xy}} = {\rm{ }}\frac{{Co{v_{xy}}}}{{{{\hat \sigma }_x}{{\hat \sigma }_y}}}$$

注意：

• 如果 $X$ 是一个正态分布的随机变量，则 $\hat S_x$ 和 $\hat K_x -3$ 的分布渐近为均值为零、方差分别为 $6/T$ 和 $24/T$ 的正态分布。
• 定义 $\hat K_x -3$ 为超额峰度（excess kurtosis）。与正态分布相比，$\hat K_x>3$ 的分布呈现出 尖峰（leptokurtic）厚尾（fat-tailed） 的特征，也就是存在更多的极端值。
• 统计量是样本的函数，样本不同统计量也不同，因此 统计量本身也是一个随机变量 ；
• 统计量的分布称为 抽样分布（sample distribution），它与随机变量 $X$ 所服从的 总体分布（population distribution） 是两个不同的概念。比如根据中心极限定理，不论 $X$ 服从哪种分布，在一定条件下，样本均值 $\bar x$ 都将渐近服从正态分布 $N\left(\mu,\sigma^2/N\right)$。

1.4 统计推断

• 定义：根据样本判断关于总体分布 $X\text{～}F\left(x\right)$ 的假设是否正确。
• 分类：
  
  • 参数检验：给定总体分布的类型，检验对分布参数的假定是否正确
    $$H_0:\theta \in \Theta$$
  • 分布检验：检验对总体分布类型的假定是否正确
    $$H_0:X\text{～}F\left(x\right)$$

2. R语言实现

2.1 概率函数

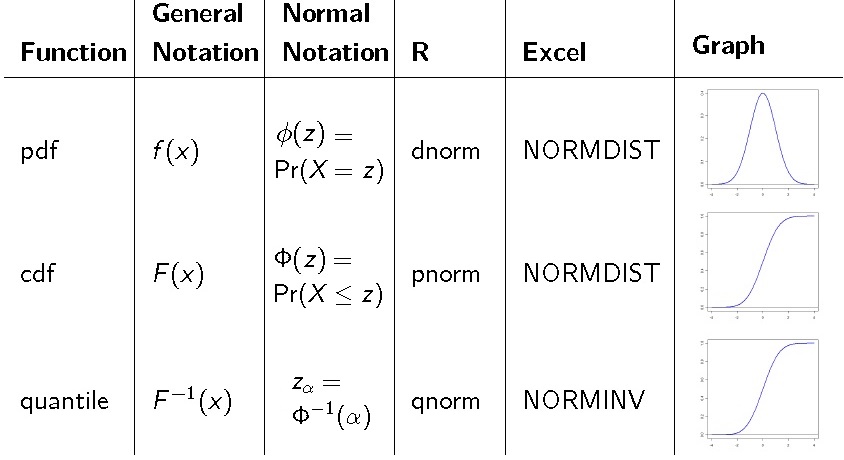
四种前缀（以正态分布 $x\text{～} N\left(\mu,\sigma^2\right)$ 为例）：

• d: 概率密度函数或频率函数dnorm(x,mu,sigma)
• p: 累积分布函数pnorm(x,mu,sigma)
• q: 给定概率 $\alpha$，求累积分布的右侧分位点qnorm(1-alpha/2,mu,sigma)
• r: 生成随机数rnorm(N,mu,sigma)

课堂讨论：借用下图说明R命令的含义

dnorm(2,0,1)
pnorm(2,0,1)
qnorm(1-0.05/2,0,1)
rnorm(5,0,1)

x <- seq(from = -5, to = 5, by = 0.01)            # 横轴向量
y <- dnorm(x)                                     # 正态分布的概率密度函数
plot(x=x,y=y, type="l",col="seagreen",lwd=2,
  xlab="x",ylab="density\ny = dnorm(x)")
grid(col="darkgrey",lwd=2)
title(main="概率分布(PDF)")
y <- pnorm(x)                                     # 正态分布的累积分布函数
plot(x=x,y=y,type="l",col="seagreen",lwd=2, xlab="x = qnorm(y)",
   ylab="probability\ny = pnorm(x)")  ; grid(col="darkgrey",lwd=2)
title(main="累积分布(CDF)")
set.seed(1)
x <- rnorm(100, sd=3)                             # 模拟生成单变量
y <- rnorm(100, mean=1) + x
mn = apply(cbind(x,y), 2, mean)                   # 计算x和y的均值
covmat= cov(cbind(x,y))                           # 计算x和y的协方差
simdata=rmnorm(300,mean=mn,varcov=covmat)         # mnormt包中函数，模拟生成双变量
ggplot(as.data.frame(simdata), aes(x=x, y=y)) +
  geom_point() +geom_smooth(method="lm") + theme_bw()

2.2 统计描述

library(MASS)
data(Insurance)                                  # 调用保险数据
str(Insurance)                                   # 查看数据结构
attach(Insurance)                                # 绑定数据

• 单变量统计描述

# 1）连续变量
mean(Holders)                                    # 基本统计量，有缺失值时用 mean(Holders, na.rm = TRUE)
median(Holders)
sd(Holders)
var(Holders)
quantile(Holders)                                # 四分位值
quantile(Holders,seq(0,1,0.1))                   # 十分位值
library(Hmisc)
describe(data.frame(District, Group, Age))       # 简单数据描述
describe(data.frame(Holders, Claims))
library(fBasics)
basicStats(data.frame(Holders, Claims))          # 更多统计量 
# 2）离散变量
table(Age)                                       # 离散变量频率表

• 双变量统计描述

# 1）两个连续变量
cor(data.frame(Holders, Claims),use="pairwise",method="pearson") # 相关系数
cov(data.frame(Holders, Claims),use="pairwise",method="pearson") # 协方差矩阵
# 2）一个连续变量和一个离散变量
by(data.frame(Holders,Claims),Age,summary)       # 按离散变量分组，对连续变量做统计描述
# 3）两个离散变量
table(District,Age)                              # 两个离散变量频率表
detach(Insurance)                                # 解除绑定

2.3 统计推断

• 参数检验
  
  • 正态分布 $X\text{～}N\left(\mu,\sigma^2\right)$
    
    • 均值检验（$\sigma^2$ 未知）t.text()：单变量 $H_0:\mu=\mu_0$，双变量 $H_0:\mu_1=\mu_2$
    • 方差检验（$\mu$ 未知）：var.text()：单变量 $H_0:\sigma^2=\sigma^2_0$，双变量 $H_0:\sigma^2_1=\sigma^2_2$
  • 总体分布未知，单变量或双变量均值检验：wilcox.test()
• 分布检验：单变量 $H_0:X\text{～}F\left(x\right)$，双变量 $H_0:F_1\left(x\right)=F_2\left(x\right)$
  
  • Jarque-Bera $JB$ 检验 normalTest()
  • Pearson $\chi^2$ 检验 chisq.test()
  • Kolmogorov-Smirnov检验 ks.test()

3. 应用

3.1 收益率基本概念

3.1.1 资产收益率

1. $k$ 期简单净收益率(simple return)
   $$R_t[k] = \frac{P_t}{P_{t - k}}-1$$
2. $k$ 期简单毛收益率(gross return)或复合收益率(compound return)
   $$1 + {R_t}[k] = \frac{{{P_t}}}{{{P_{t - k}}}} = \frac{{{P_t}}}{{{P_{t - 1}}}}\frac{{{P_{t - 1}}}}{{{P_{t - 2}}}}...\frac{{{P_{t - k + 1}}}}{{{P_{t - k}}}} = \prod\limits_{j = 0}^{k - 1} {\left( {1 + {R_{t - j}}} \right)}$$
3. 连续复合收益率(continuous compounding return) 或对数收益率(log-return)
   $${r_t} = \ln \left( {1 + {R_t}} \right) = \ln \frac{{{P_t}}}{{{P_{t - k}}}} = {p_t} - {p_{t - 1}}$$
   $${r_t}\left[ k \right] = \sum\limits_{j = 0}^{k - 1} {{r_{t - j}}}$$

注意：

• 当净收益率很小时，近似等于对数收益率。

# 比较净收益率和对数收益率
R <- seq(-0.2,0.2,len=100)
data=data.frame(R, r=log(1+R))
ggplot(data,aes(R,r)) +
  geom_line() + 
  geom_abline(slope=1, intercept=0, color="red") +
  labs(title ="对数收益率（r）和简单净收益率（R）", x = "R", y = "r= log(1+R)") +
  theme_bw()

• 由于简单净收益率的下限为-1，因此一般不能假定 $R_t$ 服从正态分布，而对数收益率的取值为整个实数域，因此一般假定 $r_t \sim N(\mu,\sigma^2)$，相应的 $R_t$ 服从对数正态分布，均值和方差分别为：
  $$E(R_t)=exp(\mu+\sigma^2/2)-1\\ Var(R_t)=exp(2\mu+\sigma^2)[exp(\sigma^2)-1]$$

4.年化复合收益率

$${{\bar R}_t}\left[ k \right] = {\left[ {\prod\limits_{j = 0}^{k - 1} {\left( {1 + {R_{t - j}}} \right)} } \right]^{\frac{1}{k}}} - 1 \approx \frac{1}{k}\sum\limits_{j = 0}^{k - 1} {{R_{t - j}}}$$
$${{\bar r}_t}\left[ k \right] = \frac{1}{k}\sum\limits_{j = 0}^{k - 1} {{r_{t - j}}} \approx {{\bar R}_t}\left[ k \right]$$

其他相关定义：

• 资产组合收益率（$w_i$为资产权重）：
  $$R_t^p = \sum\limits_{i = 1}^N {{w_i}{R_{it}}} ,~~~r_t^p \approx \sum\limits_{i = 1}^N {{w_i}{r_{it}}}$$
• 含红利支付 $D_t$ ：
  $${R_t} = \frac{{{P_t} + {D_t}}}{{{P_{t - 1}}}} - 1,~~~{r_t} = \ln \left( {{P_t} + {D_t}} \right) - \ln {P_{t - 1}}$$
• 超额收益率（参照资产标记为0）：
  $${Z_t} = {R_t} - R_t^0,~~~{z_t} = {r_t} - r_t^0$$

## 价格为不同数据类型，计算收益率
  # 1) 向量
P <- c(265.50, 264.27, 266.49, 253.81, 269.20, 277.69, 301.22, 280.98, 312.64,
  364.03, 393.62, 398.79)
P[-length(P)]                        # P(1), P(2) ... P(T-1)
P[-1]                                # P(2), P(3) ... P(T)
R <- P[-1] / P[-length(P)] - 1       # R(t) = P(t+1)/P(t) -1
R <- diff(P) / P[-length(P)]         #        [P(t+1) - P(t)]/P(t)
r <- diff(log(P))                    # r(t) = log(P(t+t)) - log(P(t)) 
  # 2) zoo 对象
library(zoo)
z <- zooreg(P, as.yearmon("2013-01"), freq = 12)
R.z <- diff(z) / lag(z,-1)  # 指定 lag=-1
r.z <- diff(log(z))         
  # 3) xts 对象 
library(xts)
x <- as.xts(z)
R.x <- diff(x) / lag(x)     # 默认 lag=1
r.x <- diff(log(x))         
  # 4) timeSeries 对象
library(timeSeries)
r.ts= returns(P)
  # 比较上述计算结果，注意xts和timeSeries的第一期为NA
  comp= data.frame(r, r.z, r.x[-1], r.ts[-1])  # 四种结果列为数据框
  round(comp,3)                                # 保留3位小数

3.1.2 债券收益率

记债券价格为 $B$、利息为$C$、面值（par value）为$F$。

1. 票面利率
   $$\text{coupon rate} = \frac{C}{F}$$
2. 当期收益率
   $$\text{spot return} = \frac{C}{B}$$
3. 到期收益率 $r$（yield to maturity, YTM）
   $$B = \frac{C_1}{1+r} + \frac{C_2}{(1+r)^2} + ... + \frac{C_T+F}{(1+r)^T}$$

3.1.3 汇率升(贴)水率

$$r_t = \frac{E_t}{E_{t-1}}-1$$

# 计算股票、债券、汇率的收益率
library(quantmod)
loadSymbols("AAPL")                            # 苹果股票
loadSymbols("^TNX")                            # 10年期美国国债收益率
loadSymbols("DEXUSEU",src="FRED")              # 汇率，1欧元等于E美元
# 如果无法直接下载，可通过 load("price.Rdata") 调用数据
chartSeries(AAPL,theme="white",TA=NULL)        # 股价，TA=NULL则不包括成交量
AAPL.rtn=diff(log(AAPL$AAPL.Adjusted))         # 经调整的股价对数收益率
chartSeries(AAPL.rtn,theme="white")
chartSeries(TNX,theme="white")
TNX.rtn=diff(TNX$TNX.Adjusted)                 # 债券收益率(%)的变化率
chartSeries(TNX.rtn,theme="white")
chartSeries(DEXUSEU,theme="white")
USEU.rtn=diff(log(DEXUSEU$DEXUSEU))            # 汇率变化率
chartSeries(USEU.rtn,theme="white")

3.2 资产收益率的特征事实

根据 Fan and Yao(2015) 资产收益率具有以下典型特征：

• 平稳性(stationarity)：$r_t$ 有稳定的均值和有限的方差
• 厚尾性(heavy tails)：峰度 $\hat K>3$，与正态分布相比呈现出尖峰厚尾的特征，说明出现爆涨和爆跌的概率大于正态分布。
• 非对称性(asymmetry)：$r_t$ 的分布呈现负偏（negatively skewed）特征，说明市场下跌比上涨的程度大。
• 波动集聚性(volatility clustering)：指市场会连续大幅上涨(或下跌)。
• 加总高斯性(aggregational Gaussianity)：当时间跨度上升时，相应的收益率会趋向正态分布，如年收益率与月收益率和日收益率相比，更接近于正态分布。
• 长期记忆性(long-memory properties)：即各期收益率之间存在相关性。
• 杠杆效应(leverage effect)：当收益率为负（即股价下跌）时，企业杠杆率上升、风险上升，股票波动性也随之上升，这种收益率和波动性变化率之间的负相关关系被称为杠杆效应。

# 以苹果的对数收益率为例
x=as.data.frame(AAPL.rtn)[,1]  
# 或者用 Tsay(2013)中3M公司数据
url="https://faculty.chicagobooth.edu/ruey.tsay/teaching/introTS/ch1data.zip"
download.file(url, "ch1data.zip")                           # 下载存为同名文件
x=read.table(unz("ch1data.zip","d-mmm-0111.txt"),header=T)  # 读入数据
x=x[,2]                                                     # 去掉日期
# 1) 作图                  
hist(x,nclass=30)                                           # 直方图
d1=density(x,na.rm=T)                                       # 密度
plot(d1$x,d1$y,xlab='rtn',ylab='density',type='l')          # 密度线
rangex=range(x,na.rm=T)                                     # 取值范围
seqx=seq(rangex[1],rangex[2],.001)                          # x轴间隔0.001
y1=dnorm(seqx,mean(x,na.rm=T),stdev(x,na.rm=T))             # 正态分布
lines(seqx,y1,lty=2)                                        # 添加正态分布线
# 2) 检验
library(fBasics)
basicStats(x) 
mean(x,na.rm=TRUE); var(x,na.rm=TRUE); stdev(x,na.rm=TRUE); 
t.test(x)                                                   # 均值检验 H0: x=0 
normalTest(x,method='jb',na.rm=T)                           # 正态分布检验，JB-test
s3=skewness(x,na.rm =T)
T=length(x) 
t3=s3/sqrt(6/T)                     
pp=2*(1-pnorm(t3))                                          # 偏度检验(Skewness test)
s4=kurtosis(x,na.rm =T)
t4=s4/sqrt(24/T) 
pp=2*(1-pnorm(t4))                                          # 峰度检验(Kurtosis test)

参考文献

1. 范剑青、姚琦伟著：The Elements of Financial Econometrics(计量金融精要)，科学出版社，2015
2. 黄文、王正林编著：《数据挖掘：R语言实战》，电子工业出版社，2014
3. R.I. Kabacoff著：《R语言实战（第2版）》，王小宁、刘撷芯、黄俊文译，人民邮电出版社，2016
4. R.S. Tsay著：《金融数据分析导论：基于R语言》，李洪成等译，机械工业出版社，2013
5. Yollin, G.: R Programming for Quantitative Finance, Lecture Notes